Scroll to:
Enhancing the performance of integer models for addressing the long-term production planning problem in open pit mines by decision variable fixation based on parametric analysis of the final pit limit
https://doi.org/10.17073/2500-0632-2023-09-156
Abstract
The importance of strategic mine planning to ensure the long-term viability of mining projects has increased significantly because of the limited availability of high-grade ore deposits. Given its high-dimensional and combinatorial nature, developing a precise mathematical optimization technique to solve the entire problem remains challenging, particularly for real-size block models. The primary objective of this study was to propose a method that combines a nested pit strategy with integer programming (IP) models to overcome computational limitations by reducing the problem’s complexity, decreasing solution times, and providing insights into alternative production schedules for large-scale open-pit mines. The proposed algorithm strategically fixes the decision variables based on parametric analysis of the ultimate pit limit to simplify the IP model. The approach was applied to various block models from MineLib, and the results were compared with standard IP solutions and findings from related studies using alternative algorithms. Applying the proposed method demonstrated significant reductions in the solution time (up to 95%) and the ability to solve intractable models.
Keywords
For citations:
Hasozdemir K., Erçelebi S. Enhancing the performance of integer models for addressing the long-term production planning problem in open pit mines by decision variable fixation based on parametric analysis of the final pit limit. Mining Science and Technology (Russia). 2024;9(2):74-84. https://doi.org/10.17073/2500-0632-2023-09-156
Enhancing the performance of integer models for addressing the long-term production planning problem in open pit mines by decision variable fixation based on parametric analysis of the final pit limit
Introduction
Open-pit mining refers to the method of extracting valuable materials from the earth's surface by excavation with the intention of generating financial gain through their subsequent sale. A mining project's economic sustainability is heavily reliant on the careful
control of this process. To enhance the manageability of this procedure, the mineral deposit is partitioned into discrete units known as blocks, which are typically modest in size and may not necessarily exhibit cubic dimensions. Each individual block inside the dataset contains distinct properties pertaining to the ore body, including the quantity of ore present, the quantity of waste material, the grade of the valuable mineral contained within, and the anticipated value of this mineral following the process of extraction. Geostatistical approaches are employed to determine these properties. The block model, as depicted in Fig. 1, is a representation of an orebody that has been partitioned into discrete blocks. This modeling approach has gained significant traction in the field of computer optimization [1].
Open-pit mine production scheduling (OPMPS) includes determining which blocks, within the final pit limit, should be mined each year and where the blocks should be transported, such as to a mill, trash dump, or stockpile, in order to maximize net present value (NPV) [1]. Long-term production planning for open-pit mine operations plays a key role in the assessment of mining projects. An important contribution in this field is presented in [2], wherein an algorithm developed that utilizes graph theory and dynamic programming to identify the ultimate pit limit that maximizes revenue. Furthermore, it is necessary to take into account various operational limitations when addressing this scheduling problem.
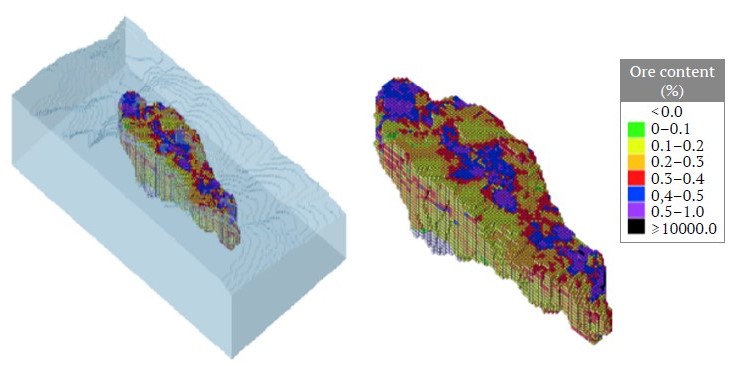
Fig. 1. Example Block Model
One instance of constraints that are commonly referred to as spatial precedence constraints, geometric sequencing constraints, or wall slope constraints is employed to guarantee the stability of excavated blocks by preventing inward collapse of the deposit. Alternatively, it is imperative that a specific block not be subjected to excavation prior to the removal of the blocks placed above it. Fig. 2 illustrates the implementation of precedence constraints, requiring excavation of blocks 1 to 9 either in earlier stages or concurrently with block 10.
This article is organized in the following manner: In Section 1, a comprehensive integer programming model is introduced to address the open-pit mining scheduling problem. Section 2 provides an overview of relevant literature to this subject. Section 3 of the paper presents a flowchart outlining the proposed method along with detailed specifications of the sample block models. The numerical outcomes of the proposed methodology are presented in Section 4, where its effectiveness is assessed based on the observed reductions in solution times. The concluding section enumerates the limitations inherent in the proposed methodology and presents prospective possibilities for future academic research.
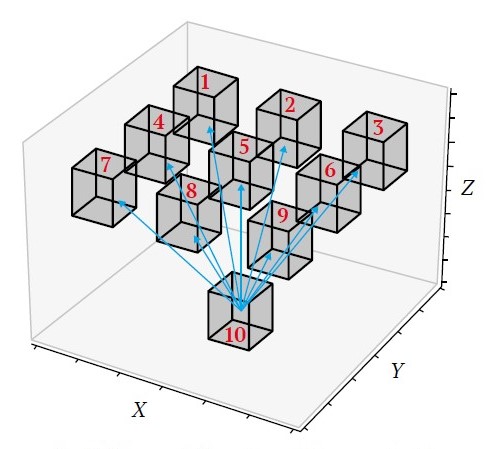
Fig. 2. Representation of precedence constraints
1. General Integer Programming model of OPMPS problem
The ultimate pit consists of N blocks, and the planning horizon is T time periods. A discounted cash flow of cit units will be obtained by the extraction of block i within the period t, r is the discount rate and A represents the block attributes such as ore tonnage and waste tonnage. Each block i is assigned a value qia for each attribute a ∈ A. uit provides an upper bound on the amount of tonnage that can be excavated in the time period t. Each block i must consider a smaller set of predecessor blocks Si (see Fig. 2).
Objective Function:
Subject to:
Eq. (2) is the objective function and attempts to maximize the net present value of the mining operation. Eq. (3) enforces the capacity constraints. Eq. (4) enforces the rule that each block must be excavated once and remain excavated. Finally, precedence constraints are enforced using Eq. (5). xi0 = 0 implies that none of the blocks in the ultimate pit is excavated before the planning horizon in Eq. (6). The decision variables of the model are binary, so they can be 1 if block i is mined in period t and 0 otherwise, Eq. (7). This basic formulation of the OPMPS problem contains NT binary variables. The major challenge in solving OPMPS is that the model instance contains many blocks and time periods, and each block-time period combination has associated binary decision variables to capture the more realistic constraints requiring all previous blocks to be extracted before removing any subsequent blocks. The application of integer models to address the problems of long- and medium-term production planning in open-pit mines is sometimes limited by difficulties such as the inability to find a solution or prolonged time required to find a solution, particularly when dealing with large-scale mineral deposits. This paper proposes a hybrid solution that combines nested pit methodology with ILP as an option to eliminate the aforementioned issues. The aim of the proposed algorithm is to fix the decision variables of the integer programming (IP) model using nested pit limits generated through parametric analysis. This approach yields efficient outcomes and reduces problem complexity. The next section outlines the phases of the proposed algorithm.
2. Literature Review
The conventional approach employed in addressing the OPMPS problem involved dividing the primary problem into smaller sub-problems, which were subsequently addressed individually [3]. The sub-problems, outlined in Fig. 3, include determining the ultimate pit limit, constructing nested pits based on ore selling price and applying a revenue adjustment factor, establishing push-backs as depicted in Fig. 4, and developing a production scheduling plan [4, 5].
Despite the utilization of this approach by the planners thus far, there are limitations as well.
- When the sub-problems are combined, it is possible that the optimal solutions obtained from these sub-problems may not result in an optimal solution for the main problem.
- The time value of money is not considered in the evaluation.
- The use of a fixed cut-off grade in the planning process has a negative impact on the economic reliability of the production schedule.
Pushbacks are a crucial component in the long-term planning process for open-pit mines, as they play a vital role in determining the final design of the mine and the profitability of the operation. They serve as a guide for the temporary production scheduling stage, delineating the start and end points of the extraction process. Moreover, pushbacks ensure the safety of the pit walls, help meet the required ore production levels, and provide a minimum operational width to accommodate mining equipment and access to the mine for other activities.
The methodology in order to obtain a series of nested pits [6]:
- A set of blocks denoted as B.
- Set B represents the final pit of the deposit.
- Nested pits are generated using a metal price parameterization and an economic block model.
- Parameterization corresponds to a sequence of N revenue factors 0 < λ1 < λ2 < ... < λN ≤ 1, which scales the metal price and each RAF produces a pit.
RAF is a variable which when multiplied with other pit optimisation parameters such as metal price, will produce the different nested pit outlines at different factoring.
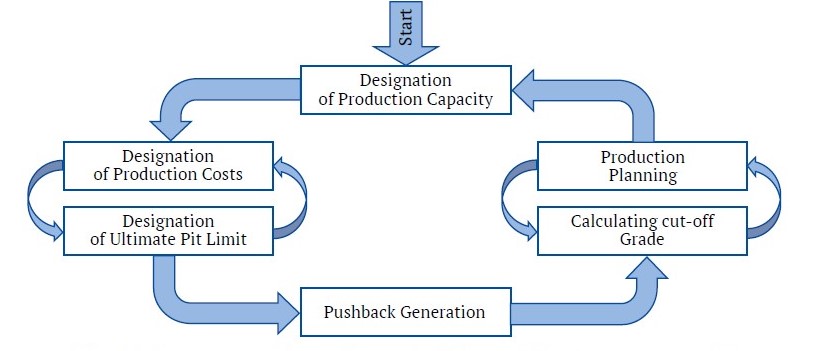
Fig. 3. Schematic view of the production scheduling problem of open pit-mines [3]
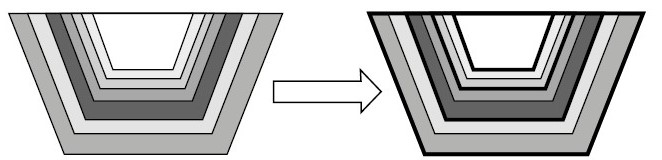
Fig. 4. Pushbacks (left), The chosen pit shells for the long-term schedule (right)
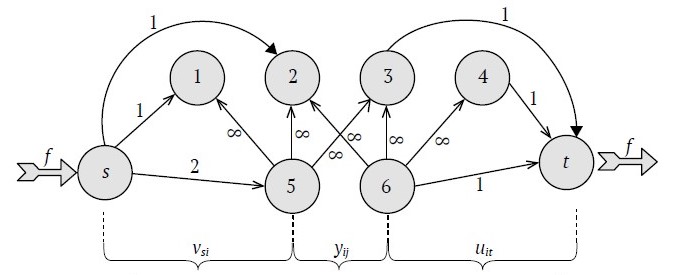
Fig. 5. Network view of the open pit mine (with nodes and edge capacities)
In [7], it was determined that the designation of ultimate pit problem can be equivalently framed as the task of identifying the most valuable path within a graph denoted as G = (S, E, W). S – is number of nodes, E is number of edges and W is the weight of the edges of the graph (Fig. 5). The problem here is to find a set of nodes (set of tasks) with a maximal value and which respect the precedence relations. Such problem is usually solved using a maximal flow algorithms.
[8] showed that the ultimate pit problem is equivalent to the maximum closure problem, which in turn, can be reduced to the min cut problem. This allows one to use known efficient algorithms for maximum flow to find the ultimate pit. The mathematical model of the maximum closure algorithm is given below [9]. Objective function, given in eq. (8), is maximization of the total value of the closure and Constraint (9) identify the precedence constraints. xi gets the value of 1 if node i is in the closure, 0 otherwise (eq. 10).
Subject to:
where Zi is the set of the successors of node i; ci is the value of node i.
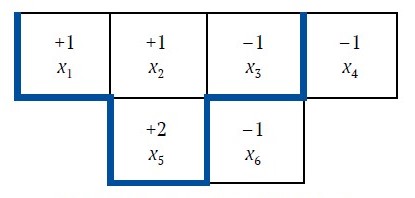
Fig. 6. Ultimate pit limit (Bold lines)
[10–12] presented a solution to address the pit limit problem (Fig. 6) by utilizing established efficient algorithms for the min cut problem. Their work demonstrates that the LG algorithm can be employed as a network flow algorithm, frequently referred to as the pseudoflow algorithm. The authors demonstrated the process of obtaining an ideal network flow using a succession of normalized trees. The researchers also conducted an analysis of the runtime of the LG method and made enhancements using scaling strategies that differ from those employed in generating pushback designs. Their findings demonstrate that LG can be implemented to operate with a time complexity of O (mn log n), where m represents the number of arcs and n represents the number of nodes.
[13] used the Bienstock-Zuckerberg algorithm in order to improve the Lagrangian relaxation approach that is used in solving the MIP models of the OPMPS problem. [14] proposed a combination of maximum flow and genetic algorithms that try to solve this problem under uncertainty. First, the final pit limit was determined by the maximum flow algorithm on the block model created according to the values obtained from the simulated ore deposits regarding different economic values. Then, the production planning of the blocks within this limit is obtained by the genetic algorithm. They applied penalties for the constraints that were not satisfied by the maximum flow algorithm. They shared their results by applying the proposed model to a copper and a gold mine. Some researchers have attempted to enhance the resilience and adaptability of long-term plans by using stochastic methods to address uncertainties in variables such as ore grades, processing capacities, and market conditions. [15] incorporated geological variability and grade uncertainty into the production scheduling optimization process using conditional simulation and stochastic integer programming (SIP). [16] offered an integrated approach to generate schedules under geological uncertainty for mining complexes with multiple processing and transportation alternatives.
Metaheuristic approaches such as the tabu search, genetic algorithm, bat algorithm, gray wolf algorithm, firefly optimization, and particle swarm optimization are used to solve the OPMPS problem and obtained results are compared with classical methods in [17–20].
3. Proposed algorithm for solution time improvement
The proposed method aims to reach the optimum or near-optimal solutions in a shorter time by narrowing the solution space of the problem by strategically fixing the decision variables of the IP model of the OPMPS problem. The decision process utilized to fix the decision variables in this context is based on nested pits generated by the parametric analysis of the ultimate pit limit. The conventional approach involves representing the economic block model of a mineral deposit as a network based on graph theory. Subsequently, this network is subjected to analysis using maximum flow algorithms to find the ultimate pit limit, which corresponds to the production volume that yields the highest income. The next phase involves subjecting the blocks within the ultimate pit limit to a maximum flow analysis. This analysis entails recalculating their economic values based on the Revenue Adjustment Factor (RAF), resulting in the generation of progressively smaller open pit boundaries. The aforementioned boundaries are commonly referred to as nested pits.
In the procedure outlined above, the selection of the RAF involves incrementing it by 0.01, often within the range of 0.2 to 1, in order to establish an approximate calculation for 80 nested pit limits. Afterward, the calculation of the quantity of ore and waste material, the grade of the valuable mineral, and the economic value resulting from the excavation of these nested pits are performed. Following this computation, the open pit limits providing the annual production capacity are selected to represent the longterm production plan, and a determination is then performed to solve the open pit production planning problem. One significant issue associated with this method pertains to the considerable changes in the open pit limits, which are determined based on the income adjustment factor. Once a certain threshold is reached, these boundaries undergo rapid changes in size. As a result, the quantity of material available between two consecutive limits usually exceeds the annual production capacity by a significant amount. In academic literature, this situation is known as the gap problem. Fig. 8 provides a numerical illustration of this situation. The histogram depicted in Fig. 7 illustrates that the parametric analysis yields a minimum final pit limit of 18 blocks, whereas the nearest second-largest quarry contains 3049 blocks. The gap problem refers to the absence of an appropriate quarry boundary that can be chosen for the initial period while utilizing the conventional planning method.
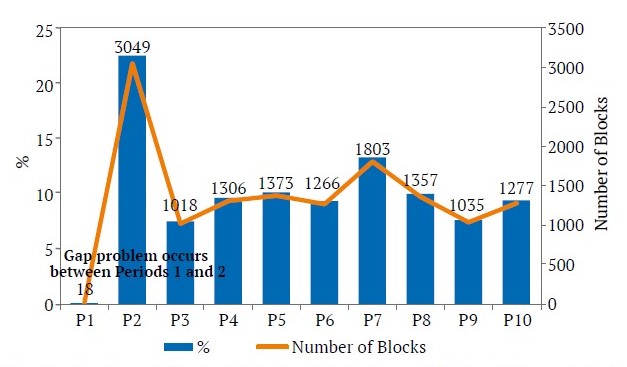
Fig. 7. The Gap Problem is illustrated by the distribution of blocks within nested pit shells
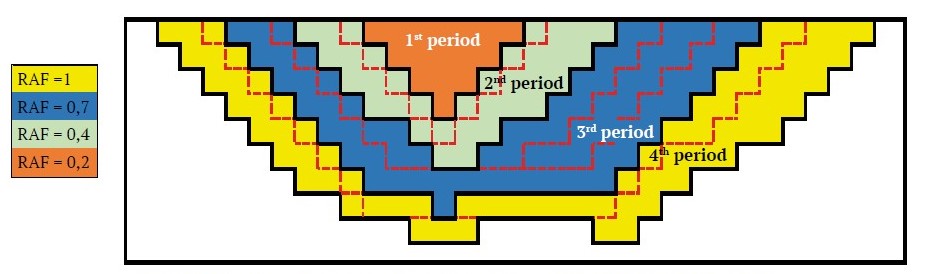
Fig. 8. 2D section of example nested pits (with candidate pit shells for periods)
This paper proposes a hybrid solution that combines the nested pits methodology with IP as an option for reducing the aforementioned issues. The aim of the proposed algorithm is to fix the decision variables of the integer programming (IP) model using the nested pit limits generated through parametric analysis. The act of decision variable fixing in the context of integer programming refers to the predetermination of certain decision variables, which ultimately dictates the production scheduling of open-pit mining operations within predetermined boundaries. This approach yields efficient outcomes, reducing the problem's model complexity. The next section outlines the phases of the proposed algorithm.
Algorithm
1. Utilization of Hochbaum's pseudoflow algorithm to determine the limit of the ultimate pit.
- The outermost pit shell in Fig. 8 (all blocks within the outermost pit limit, obtained by RAF = 1).
- The generation of nested pits by the utilization of parametric analysis on the blocks located within the boundaries of the ultimate pit, employing the RAF (see Fig. 8).
2. Computation of the material quantities within the nested pits, as well as the identification of potential pit shells that can fulfill the intended annual production capacity (see Fig. 8).
- The innermost pit limit is the candidate pit shell for the first period. (Orange blocks, obtained by RAF = 0.2). The second pit limit is the candidate pit shell for the second period. (Green blocks, obtained by RAF = 0.4).
3. In each time period, the decision variables of the blocks located beyond the limits of the nested pit that have been identified as candidates for that specific period are fixed (Figs. 9, 10).
- For example, for T = 4 periods, the xi1 variables of the gray blocks are fixed at 0, because the orange blocks represent the candidate pit shell for the 1st period and yield the highest income with a sufficient amount of ore within themselves (Fig. 9). Another example can be seen in Fig. 10. xi2 variables of gray blocks are fixed at 0, so blocks that will be excavated during the second period of production will be searched within the green limit because there is sufficient ore for the processing capacity and they yield the highest income.
4. A different strategy is implemented to fix variables in the context of ore abundance within a candidate shell over a certain time period. In this procedure, if there is an excess amount of ore within the shell, the decision variables of the blocks within that shell are fixed at 1, as those blocks are expected to be excavated in subsequent periods i.e. xi5, variables associated with pink blocks in Fig. 11 are fixed as 1 implying that they are expected to be excavated at the end of T = 5).
5. The final process for fixing variables is implemented as follows: if the amount of ore in a candidate shell is less than the ore production capacity, the decision variable for all blocks within that shell is fixed at 1 since these blocks can be excavated within that time frame. (Blue blocks in Fig. 11).
6. Solving the problem with reduced size, which is obtained by fixing the decision variables.
The block models in Table 1 were obtained from MineLib, a widely used dataset in the mining industry.
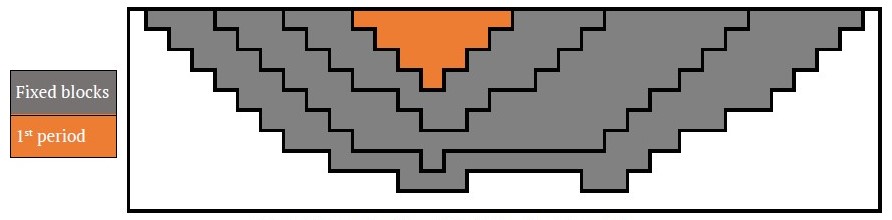
Fig. 9. Example of variable fixing for 1st period
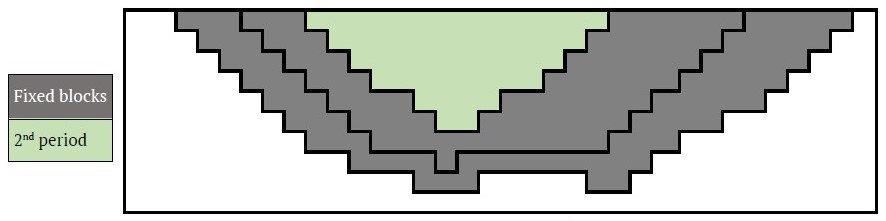
Fig. 10. Example of variable fixing for 2nd period
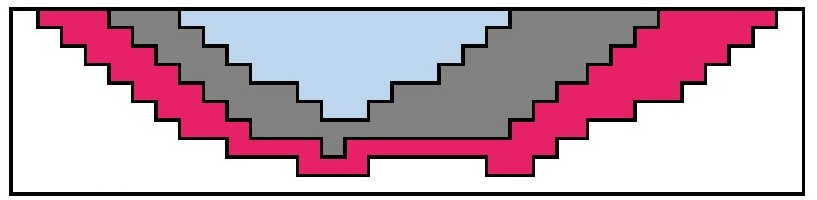
Fig. 11. Variable fixing in the context of ore abundance (pink blocks) and inadequacy of ore (blue blocks)
Table 1
Block model specifications
| ID | # of blocks | # of blocks within UPL | # Binary Variables | Ore capacity | Ore capacity | Periods T |
| zuck_small | 9,400 | 8,752 | 122,528 | 20M | 10% | 14 |
| kd | 14,153 | 13,258 | 132,580 | 10M | 10% | 10 |
| zuck_medium | 29,277 | 29,230 | 263,880 | 8M | 10% | 9 |
| marvin | 53,271 | 5,324 | 69,212 | 20M | 10% | 13 |
| zuck_large | 96,821 | 96,821 | 968,210 | 3M | 10% | 10 |
| mclaughlin | 2,140,342 | 112,687 | 1,126,687 | 3.5M | 10% | 10 |
4. Numerical results obtained by suggested method
The proposed methodology for reducing the solution time of the OPMPS problem is implemented on six different block models obtained from MineLib. MineLib is comprised of various example block models utilized to demonstrate the performance of various algorithms proposed for the solution of the OPMPS problem. The results are given in the following fashion: First, the block models were tried to be solved without any decision variable fixing, and results were tried to be obtained. After that, the proposed method is applied to the same block model, and improvements in solution times are investigated. The GUROBI solver is used for solving the IP models. Optimality gap relaxation is set to %1, and the upper bound for the operating time is set to 36,000 seconds. The GUROBI solver is using the Barrier Method to designate the upper bound of the LP relaxation. Table 2 depicts the numerical results of the suggested method and its comparison with the standard IP model. The acronym “Nstl” denotes the absence of a solution within the designated time limit, whereas “memory” refers to the situation when the computational technique for solving the model surpasses the computer's available memory capacity. “%inf” indicates that the decrease in solution time could not be measured because the standard IP model was unable to solve the problem within the given time limit or exceeded the RAM capacity of the PC.
As can be seen from Table 2. By applying the suggested technique to various block models, we were able to observe significant improvements in the duration of the solution time. This demonstrates the effectiveness and practicality of the proposed method in real world scenarios. In the mean time, some of the problems that can not be solved with the general IP model have been solved with the proposed method which depicts the efficiacy of the suggested method. By means of NPV of the solution, there are some decrease on the NPV amount which is a drawback of the suggested methodology. This situation arises due to the limitation of solution alternatives with nested pit boundaries. The decline in net present value (NPV) may be deemed acceptable in the context of solving complex block models of significant scale that are infeasible to solve. An additional limitation of the proposed algorithm is its reliance on the existence of constraints concerning the capacity of ore production. The solutions derived from this methodology may turn out to be unfeasible when there are constraints on the total production capacity. To address this limitation, one potential solution is to incorporate relaxation techniques into the Integer Programming (IP) model. This would allow for the inclusion of total production capacity limitations within the objective function through the utilization of Lagrange Multipliers. Additionally, it is possible to use various heuristic approaches to ensure compliance with the limitations on total production capacity following the resolution of the integer programming (IP) model using the suggested strategy.
Table 2
Numerical Results
| ID | Solution time of standard ILP model (sec) | NPV of standard ILP model | Optimality Gap | Solution Time of the suggested algorithm | NPV of suggested algorithm | Optimality Gap | Decrease in solution time |
| zuck_small | 2,688 | 827.4M | 1.79% | 110 | 815.2M | 0.60 % | –95 % |
| kd | 2,806 | 413.2M | 0.15% | 177 | 405.7M | 0.98 % | –93 % |
| zuck_medium | 23,110 | 721.3M | 1.7% | 428 | 706.3M | 0.88 % | –98 % |
| marvin | 1,471 | 799.5M | 0.98% | 71 | 798.3M | 0.96 % | –95 % |
| zuck_large | Nstl | Nstl | Nstl | 2,221 | 76.9M | 0.08 % | %inf |
| mclaughlin | Memory | Memory | Memory | 3,332 | 1,031.2M | 0.16 % | %inf |
The graphical results of the Marvin block model are displayed in Fig. 12, with the intention of enabling a comparison between the suggested methodology and the traditional IP model. It is apparent that similar results can be attained within a shorter timeframe through variable fixing. The outcomes of the proposed algorithm are additionally compared with the results achieved by the modified TopoSort algorithm in [11] and the Bienstock & Zuckerberg algorithm in [21] as illustrated in Table 3. The TopoSort findings are the most optimal and feasible known outcomes of the relevant block models. The algorithm proposed by Bienstock and Zuckerberg yields a better net present value (NPV); nonetheless, these results are deemed infeasible.
Based on the findings shown in Table 3, the proposed methodology demonstrates notable efficacy in addressing the OPMPS problem while also exhibiting the potential to enhance the maximum achievable NPV for certain block models, as reported in MineLib [22].
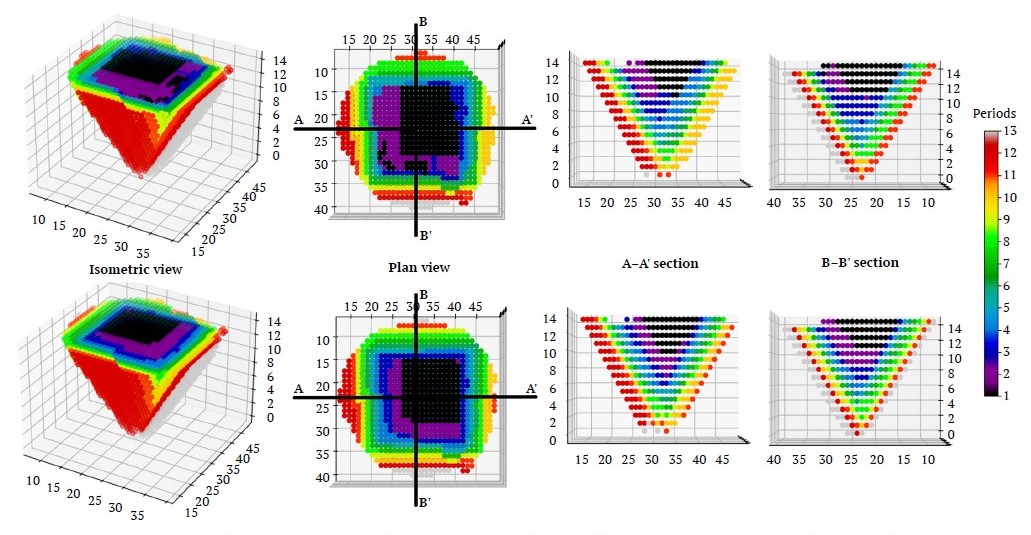
Fig. 12. Example comparison of scheduling results of Marvin block model (conventional IP result (top), IP result with fixed variables (bottom))
Table 3
NPV comparison of the suggested algorithm with related studies
| Block Model | TopoSort | Bienstock & Zuckerberg | Предлагаемый алгоритм |
| mclaughlin | 1073.3M | 1079.0M | 1031.2M |
| marvin | 820.7M | 863.4M | 798.3M |
| zuck_medium | 615.4M | 710.6M | 706.3M |
| kd | 396.8M | 409.4M | 405.7M |
| zuck_small | 788.6M | 854.2M | 815.2M |
Conclusion and future study suggestions
Open-pit mining plays an essential part in the socio-economic progress of nations and the advancement of technology, as it provides the extraction of valuable minerals that serve as the building blocks of these advancements. The achievement of cost-effective mining operations necessitates the implementation of a strategic planning approach. Within this particular context, many researchers have proposed alternative approaches to address the issue of open pit mining production scheduling. The primary aim of this scheduling procedure is to maximize the net present value. The methods represented in this field consist of maximum flow algorithms, linear programming, integer programming, dynamic programming, metaheuristic methods, and simulation techniques. While these strategies have proven to be successful in addressing small or medium-sized ore deposits, their efficacy and efficiency are limited when it comes to handling larger mineral deposits. This paper presents a recommended alternative approach aimed at overcoming the challenges associated with the implementation of existing approaches in the context of large mineral resources. Traditionally, the OPMPS problem has been solved by manually picking those that meet the annual production capacity from the nested open pit boundaries generated from the mineral deposit’s parametric analysis. The objective of this study is to decrease the problem size by constraining some decision variables of the integer programming model using limits derived from conventional approaches. This approach aims to address the challenges associated with resolving block models of mineral deposits that are either unsolvable or require excessive time to resolve within a limited timeframe. The efficacy of the suggested method has been demonstrated through its application to sample block models in the existing literature. The acquired findings demonstrate that the suggested method not only significantly reduces the solution time by up to 95% but also enables the solving of models that were previously unsolvable due to limited computational resources. Although the decrease in NPV for some models may appear to be a drawback of this method, it is a significant contribution to the mining industry that various production plan alternatives can be examined in a short period of time based on varying mining capacities and ore sales prices.
Future research possibilities include the incorporation of parameters such as ore grade, vertical rate of advance, and minimum mining width, which should be considered during mining operations, into the planning procedure. The incorporation of operational factors, such as the minimum mining width, can be achieved by integrating them as relevant constraints inside the parametric analysis phase of the proposed method. By using this approach, candidate shells for the periods would meet the given constraints prior to solving the integer programming (IP) model. In addition, further research could explore the effects of techniques employed to meet the constraints of total production capacity. Furthermore, it is worth considering the inclusion of metaheuristic approaches as potential avenues for future research. These methods, although challenging to develop a viable production plan initially, can be explored in subsequent studies where the initial results obtained from the proposed method are utilized and the net present value (NPV) is enhanced through the application of various metaheuristic techniques such as simulated annealing, tabu search, and ant colony optimization.
References
1. Caccetta L., Hill S. An application of branch and cut to open pit mine scheduling. Journal of Global Optimization. 2003;27:349–365. https://doi.org/10.1023/A:1024835022186
2. Lerchs H., Grossmann I. F. Optimum design of open-pit mines. Transactions, C.I.M. 1965;LXVIII:17–24.
3. Dagdelen K., Johnson T. B. Optimum open-pit mine production scheduling by Lagrangian parameterization. In: Proceedings of the 19th APCOM. 1984;127–142.
4. Elkington T., Durham R. Integrated open pit pushback selection and production capacity optimization. Journal of Mining Science. 2011;47:177–190. https://doi.org/10.1134/S1062739147020055
5. Kumral M. Production planning of mines: optimization of block sequencing and destination. International Journal of Mining, Reclamation, and Environment. 2012;26(2):93–103. https://doi.org/10.1080/17480930.2011.644474
6. Jélvez E., Morales N., Askari-Nasab H. A new model for automated pushback selection. Computers & Operations Research. 2020;115:104456. https://doi.org/10.1016/j.cor.2018.04.015
7. Tolwinski B., Underwood R. An algorithm to estimate the optimal evaluation of an open-pit mine. In: Proceedings of the 23rd International Symposium on the Application of Computers and Operations Research in the Mineral Industries. 1992;399–409.
8. Picard J. C. Maximal closure of a graph and applications to combinatorial problems. Management Science. 1976;22(11):1268–1272. https://doi.org/10.1287/mnsc.22.11.1268
9. Tachefine B., Soumis F. Maximal closure on a graph with resource constraints. Computers & Operations Research. 1997;24(10):981–990. https://doi.org/10.1016/S0305-0548(97)00008-7
10. Chandran B. G., Hochbaum D. S. A computational study of the pseudoflow and push-relabel algorithms for the maximum flow problem. Operations Research. 2009;57(2):358–376. https://doi.org/10.1287/opre.1080.0572
11. Hochbaum D. S. The pseudoflow algorithm: A new algorithm for the maximum-flow problem Operations Research. 2008;56(4):992–1009. https://doi.org/10.1287/opre.1080.0524
12. Hochbaum D. S., Chen A. Performance analysis and best implementations of old and new algorithms for the open- pit mining problem. Operations Research. 2000;48(6):894–914. https://doi.org/10.1287/opre.48.6.894.12392
13. Muoz G., Espinoza D., Goycoolea M. et al. A study of the Bienstock-Zuckerberg algorithm: applications in mining and resource-constrained project scheduling. Computational Optimization and Applications. 2018;69(2):501–534. https://doi.org/10.1007/s10589-017-9946-1
14. Paithankar A., Chatterjee S. Open-pit mine production schedule optimization using a hybrid of maximum-flow and genetic algorithms. Applied Soft Computing. 2019;81:105507. https://doi.org/10.1016/j.asoc.2019.105507
15. Ramazan S., Dimitrakopoulos R. Stochastic optimisation of long-term production scheduling for open pit mines with a new integer programming formulation. İn: Dimitrakopoulos R. (ed.) Advances in Applied Strategic Mine Planning. Springer, Cham; 2018. Pp. 139–153. https://doi.org/10.1007/978-3-319-69320-0_11
16. Montiel L., Dimitrakopoulos R. Optimizing mining complexes with multiple processing and transportation alternatives: An uncertainty-based approach. European Journal of Operational Research. 2015;247(1):166–178. https://doi.org/10.1016/j.ejor.2015.05.002
17. Alipour A., Khodaiari A. A., Jafari A., Tavakkoli-Moghaddam R. Production scheduling of open-pit mines using genetic algorithms: a case study. International Journal of Management Science and Engineering Management. 2020;15(3):176–183. https://doi.org/10.1080/17509653.2019.1683090
18. Elsayed S., Sarker R., Essam D., Coello C. C. Evolutionary approach for large-scale mine scheduling. Information Sciences. 2020;523:77–90. https://doi.org/10.1016/j.ins.2020.02.074
19. Senécal R., Dimitrakopoulos R. Long-term mine production scheduling with multiple processing destinations under mineral supply uncertainty, based on a multi-neighborhood Tabu search. International Journal of Mining, Reclamation, and Environment. 2020;34(7):459–475. https://doi.org/10.1080/17480930.2019.1595902
20. Tolouei K., Moosavi E., Tabrizi A. H. B. et al. Improving performance of open-pit mine production scheduling problems under grade uncertainty by hybrid algorithms. Journal of Central South University. 2020;27(9):2479–2493. https://doi.org/10.1007/s11771-020-4474-z
21. Bienstock D., Zuckerberg M. Solving L. P. relaxations of large-scale precedence constrained problems. In: Eisenbrand F., Shepherd F. B. (eds.) Integer Programming and Combinatorial Optimization. IPCO 2010. Lecture Notes in Computer Science. Vol. 6080. Springer, Berlin, Heidelberg; 2010. https://doi.org/10.1007/978-3-642-13036-6_1
22. Espinoza D., Goycoolea M., Moreno E., Newman A. N. MineLib: a library of open pit problems. Annals of Operations Research. 2013;206:93–114. https://doi.org/10.1007/s10479-012-1258-3
About the Authors
K. HasozdemirTurkey
Kursat Hasozdemir – PhD-Student, Research Assistant, Mining Engineering Department
Istanbul
S. G. Erçelebi
Turkey
Selamet Gürbüz Erçelebi – Dr. Sci., Professor, Mining Engineering Department
Istanbul
Review
For citations:
Hasozdemir K., Erçelebi S. Enhancing the performance of integer models for addressing the long-term production planning problem in open pit mines by decision variable fixation based on parametric analysis of the final pit limit. Mining Science and Technology (Russia). 2024;9(2):74-84. https://doi.org/10.17073/2500-0632-2023-09-156
JATS XML




































