Перейти к:
Повышение эффективности целочисленных моделей для решения задачи долгосрочного планирования добычи на открытых горных работах путем установления переменных решений на основе параметрического анализа конечного контура карьера
https://doi.org/10.17073/2500-0632-2023-09-156
Аннотация
Важность стратегического планирования горных работ для обеспечения долгосрочной жизнеспособности горных проектов значительно возросла из-за сокращения числа месторождений богатых руд. Учитывая его многомерную и комбинаторную природу, разработка точного метода математической оптимизации для решения всей задачи остается сложной проблемой, особенно для блочных моделей в натуральную величину. Основная цель данного исследования заключалась в том, чтобы предложить метод, сочетающий стратегию вложенных контуров карьера с моделями целочисленного программирования (ЦП / ЦЛП) для преодоления вычислительных ограничений за счет снижения сложности задачи, сокращения времени решения и предоставления информации об альтернативных графиках добычи для крупномасштабных открытых разработок. Предложенный алгоритм стратегически устанавливает переменные решения на основе параметрического анализа конечного (проектного) контура карьера для упрощения ЦП-модели. Этот подход был применен к различным блочным моделям из MineLib, а результаты были сопоставлены со стандартными ЦП-решениями и результатами соответствующих исследований с использованием альтернативных алгоритмов. Применение предложенного метода продемонстрировало существенное сокращение времени решения (на величину до 95 %) и возможность решения трудноразрешимых моделей.
Ключевые слова
Для цитирования:
Хасоздемир К., Эрчелеби С. Повышение эффективности целочисленных моделей для решения задачи долгосрочного планирования добычи на открытых горных работах путем установления переменных решений на основе параметрического анализа конечного контура карьера. Горные науки и технологии. 2024;9(2):74-84. https://doi.org/10.17073/2500-0632-2023-09-156
For citation:
Hasozdemir K., Erçelebi S. Enhancing the performance of integer models for addressing the long-term production planning problem in open pit mines by decision variable fixation based on parametric analysis of the final pit limit. Mining Science and Technology (Russia). 2024;9(2):74-84. https://doi.org/10.17073/2500-0632-2023-09-156
Повышение эффективности целочисленных моделей для решения задачи долгосрочного планирования добычи на открытых горных работах путем установления переменных решения на основе параметрического анализа конечного контура карьера
Введение
Под добычей открытым способом понимается метод извлечения ценных материалов с/из-под земной поверхности путем карьерной (открытой) разработки с намерением получения финансовой выгоды за счет их последующей продажи. Экономическая устойчивость горнодобывающего проекта в значительной степени зависит от тщательного контроля этого процесса. Чтобы повысить управляемость этой процедуры, месторождение полезных ископаемых разбивается на дискретные элементы, известные как блоки, которые, как правило, имеют умеренные размеры и не обязательно имеют кубическую форму. Каждый отдельный блок в наборе данных имеет различные свойства (параметры), относящиеся к рудному телу, включая количество присутствующей руды, количество пустой породы (отходов), содержание ценного (промышленного) минерала (полезного ископаемого) в нем и ожидаемую ценность этого минерала после процесса извлечения. Для определения этих свойств (параметров) используются геостатистические подходы. Блочная модель, как показано на рис. 1, является представлением рудного тела, разделенного на дискретные блоки. Такой подход к моделированию получил значительное распространение в области компьютерной оптимизации [1].
Планирование добычи на открытых горных работах (планирование карьерной разработки) включает в себя определение того, какие блоки в пределах конечного (проектной) контура карьера должны добываться каждый год и куда эти блоки должны транспортироваться, например, на мельницу/обогатительную фабрику, в отвал или на рудный склад, чтобы максимизировать чистую приведенную стоимость (ЧПС) [1]. Долгосрочное планирование добычи на открытых горных работах играет ключевую роль в оценке проектов по добыче полезных ископаемых. Важный вклад в эту область горных наук представлен в работе [2], в которой был разработан алгоритм, использующий теорию графов и динамическое программирование для определения конечного контура карьера, максимизирующий доход. Кроме того, при решении этой задачи планирования необходимо учитывать различные эксплуатационные ограничения.
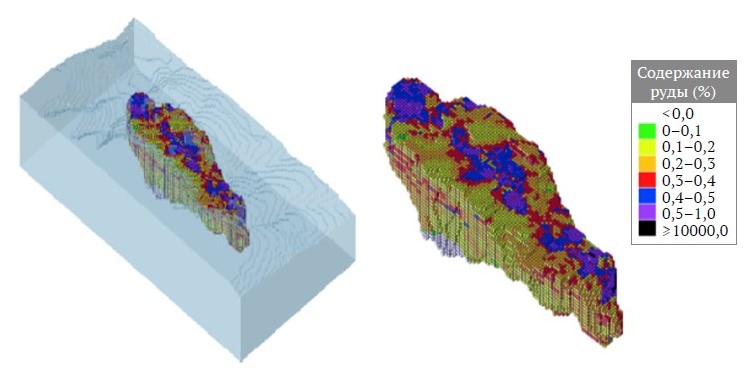
Рис. 1. Пример блочной модели
Один из вариантов ограничений, которые обычно называют ограничениями пространственной очередности, ограничениями геометрической последовательности или ограничениями угла откоса бортов карьера, используется для обеспечения устойчивости выемочных блоков путем предотвращения обрушения пород внутрь карьера. Иными словами, крайне важно, чтобы к извлечению конкретного блока переходили только после извлечения блоков, расположенных над ним. На рис. 2 показана реализация ограничений очередности, требующих выемки блоков с 1-го по 9-й либо на более ранних стадиях, либо одновременно с блоком 10.
Эта статья организована следующим образом. В разделе 1 представлена комплексная целочисленная модель программирования для решения задачи планирования открытых горных работ. В разделе 2 представлен обзор литературы, относящейся к данной теме. В разделе 3 статьи представлена блок-схема, описывающая предлагаемый метод, а также подробные спецификации образцов блочных моделей. Численные результаты применения предложенной методики представлены в разделе 4, где ее эффективность оценивается на основе наблюдаемого сокращения времени решения. В заключительном разделе перечисляются ограничения, присущие предлагаемой методологии, и представляются перспективные направления и возможности для дальнейших научных исследований.
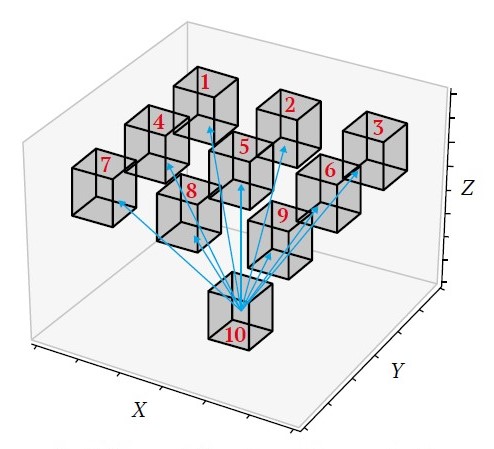
Рис. 2. Иллюстрация ограничений очередности
1. Общая целочисленная модель программирования задачи планирования открытой разработки
Конечный контур карьера включает N блоков, а горизонт планирования составляет T временных периодов. Дисконтированный денежный поток в размере cit единиц будет получен при добыче блока i в течение периода t; r – ставка дисконтирования, а A представляет собой атрибуты блока, такие как тоннаж руды и тоннаж отходов. Каждому блоку i присваивается значение qia для каждого атрибута a ∈ A. uit обеспечивает верхнюю границу количества тоннажа, который может быть извлечен за период времени t. Каждый блок i должен учитывать меньший набор блоков-предшественников Si (см. рис. 2).
Целевая функция (критерий выбора):
С соблюдением:
Уравнение (2) является целевой функцией (критерием выбора) и нацелено на максимизацию чистой приведенной стоимости горнодобывающего предприятия. Уравнение (3) обеспечивает соблюдение ограничений по имеющимся производственным мощностям. Уравнение (4) обеспечивает соблюдение правила, согласно которому каждый блок должен быть когда-то извлечен – раз и навсегда. Наконец, ограничения очередности накладываются посредством уравнения (5). xi0 = 0 подразумевает, что ни один из блоков в конечном контуре карьера не извлекается ранее запланированного срока согласно установленному горизонту планирования в уравнении (6). Переменные решения модели являются двоичными, поэтому они могут быть равны 1, если блок i извлекается в период t, и 0 в противном случае – уравнение (7). Эта базовая формулировка задачи планирования карьерной разработки содержит двоичные переменные NT. Основная сложность при решении задачи планирования карьерной разработки заключается в том, что представляющая ее модель содержит множество блоков и периодов времени и каждая комбинация блоков и периода времени имеет связанные двоичные переменные решения для учета более реалистичных ограничений, требующих извлечения всех предыдущих блоков перед извлечением любых последующих блоков. Применение целочисленных моделей для решения задач долгосрочного и среднесрочного планирования добычи на открытых горных разработках иногда ограничено такими сложностями, как невозможность найти решение или длительное время, необходимое для его поиска, особенно при работе с крупномасштабными месторождениями полезных ископаемых. В данной работе предлагается гибридное решение, сочетающее методологию вложенных контуров карьера с подходом целочисленного (линейного) программирования (ЦП/ЦЛП) в качестве варианта устранения вышеупомянутых проблем. Целью предложенного алгоритма является установление переменных решения модели целочисленного программирования (ЦП) с использованием вложенных конечных контуров (пределов, границ) карьера, полученных с помощью параметрического анализа. Такой подход дает эффективные результаты и снижает сложность задачи. В следующем разделе описаны этапы предложенного алгоритма.
2. Обзор литературы
Традиционный подход, используемый при решении задачи планирования карьерной разработки, предполагал разделение основной, главной задачи на более мелкие подзадачи, которые впоследствии решались по отдельности [3]. Подзадачи, обозначенные на рис. 3, включают в себя определение конечного контура карьера, построение вложенных контуров карьера на основе цены реализации руды и применение коэффициента корректировки дохода (RAF), установление очередей (промежуточных контуров / разносок бортов) карьера, как показано на рис. 4, и разработку плана-графика добычи [4, 5].
Несмотря на то что планировщики до сих пор применяют этот подход, у него имеются и ограничения.
- При объединении подзадач возможно, что оптимальные решения, полученные из этих подзадач, не приведут к оптимальному решению главной задачи.
- Временная стоимость денег (стоимость денег с учётом доходов будущих периодов) при оценке не учитывается.
- Использование фиксированного бортового содержания в процессе планирования отрицательно сказывается на экономической надежности/устойчивости графика добычи.
Очереди (промежуточные контуры) карьера являются важнейшим компонентом в процессе долгосрочного планирования открытых горных работ, поскольку они играют жизненно важную роль в определении окончательного проекта рудника и рентабельности отработки. Они служат ориентиром для этапа предварительного планирования добычи, выделяя начальную и конечную точки процесса выемки. Кроме того, разноски бортов обеспечивают безопасность бортов карьера, помогают поддерживать требуемые уровни добычи руды и обеспечивают минимальную рабочую ширину для размещения горного оборудования и доступа в рудник для других видов работ.
Методика получения серии вложенных контуров карьера [6]:
- Набор блоков, обозначаемый как B.
- Набор B представляет собой конечный контур карьера при разработке месторождения.
- Вложенные контуры карьера генерируются с использованием параметризации цен на металл и экономической блочной модели.
- Параметризация соответствует последовательности N коэффициентов корректировки дохода (RAF) 0 < λ1 < λ2 < ... < λN ≤ 1, что масштабирует цену металла, и каждому значению RAF соответствует отдельный контур карьера.
RAF – это переменная, которая при умножении на другие параметры оптимизации карьера, такие как цена металла, даст различные вложенные контуры карьера при разной факторизации.
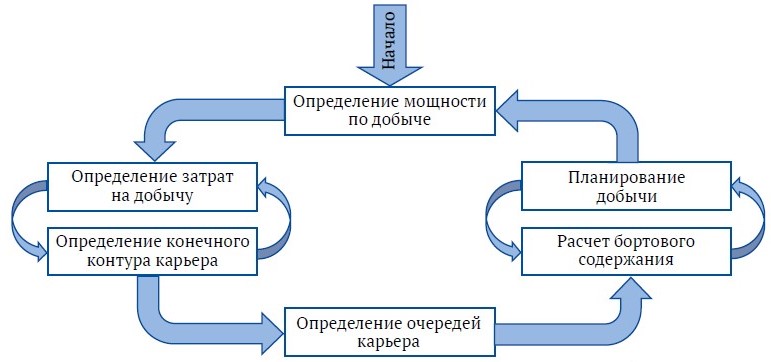
Рис. 3. Схематическое представление задачи планирования открытой разработки (карьером) [3]
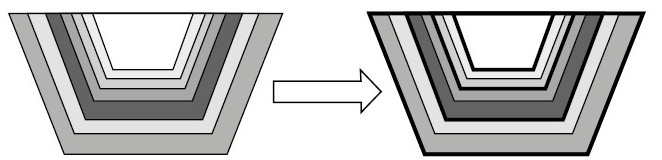
Рис. 4. Очереди (промежуточные контуры / разноски бортов) карьера (слева). Выбранные вложенные контуры карьера для долгосрочного графика разработки (справа)

Рис. 5. Карьер: ракурс сети (с узлами и мощностями ребер)
В работе [7] было определено, что обозначение задачи определения конечного контура карьера может быть эквивалентно сформулировано как задача определения наиболее ценного пути в графе, обозначенном как G = (S, E, W). S – число узлов, E – число ребер и W – вес ребер графа (рис. 5). Задача здесь состоит в том, чтобы найти набор узлов (набор задач) с максимальным значением, которые удовлетворяют условию очередности. Такая задача, как правило, решается с помощью алгоритмов поиска максимального потока (алгоритм Форда–Фалкерсона).
В [8] показано, что задача построения конечного контура карьера эквивалентна задаче максимального закрытия, которая, в свою очередь, может быть сведена к задаче минимального разреза (алгоритм Штёр–Вагнера). Это позволяет использовать известные эффективные алгоритмы максимального потока для нахождения конечного контура карьера. Математическая модель алгоритма максимального закрытия приведена ниже [9]. Целевая функция, заданная в уравнении (8), максимизирует суммарное значение закрытия, а ограничение (9) определяет ограничения очередности: i принимает значение 1, если узел i принадлежит закрытию, и 0 в противном случае (уравнение (10)):
С соблюдением:
где Zi – множество преемников (последующих элементов) узла i; ci – значение узла i.
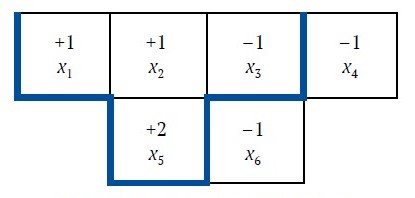
Рис. 6. Конечный контур карьера (выделенные линии)
В работах авторов [10–12] представлено решение задачи нахождения конечного контура карьера (рис. 6) с использованием устоявшихся эффективных алгоритмов для решения задачи минимального разреза. Эти исследования показывают, что алгоритм LG может быть использован в качестве алгоритма потока в сети, часто называемого алгоритмом псевдопотока. Авторы продемонстрировали процесс получения идеального потока в сети с использованием последовательности нормализованных деревьев решений. Эти исследователи также провели анализ времени, необходимого при использовании метода LG, и внесли усовершенствования, используя стратегии масштабирования, которые отличаются от тех, которые используются при разработке проектов разноски бортов карьера. Их результаты показывают, что метод LG может быть применен для работы с временной сложностью (алгоритма) O (mn log n), где m представляет количество ребер графа, а n – количество узлов.
В работе [13] использовался алгоритм Бьенстока–Цукерберга для улучшения подхода релаксации Лагранжа, который используется при решении MЦП-моделей задачи планирования карьерной разработки. В [14] предложена комбинация алгоритма поиска максимального потока и генетического алгоритма в попытке решить эту задачу в условиях неопределенности. Сначала конечный контур карьера был определен с помощью алгоритма максимального потока на блочной модели, созданной по значениям, полученным из моделей рудных залежей относительно различных экономических значений. Затем с помощью генетического алгоритма подготовили планирование извлечения блоков в пределах этого конечного контура. Авторы применяли штрафные санкции за ограничения, которые не были соблюдены при применении алгоритма максимального потока. Они поделились своими результатами, применив предложенную модель к медно-золотому руднику. Некоторые исследователи пытались повысить устойчивость и адаптивность долгосрочных планов, используя стохастические методы для устранения неопределенностей в таких переменных, как содержания в рудах, перерабатывающие мощности и рыночные условия. Авторы работы [15] включили геологическую изменчивость и неопределенность содержаний в рудах в процесс оптимизации планирования добычи с использованием условного моделирования и стохастического целочисленного программирования (СЦП). В [16] предложен комплексный подход к формированию планов-графиков в условиях геологической неопределенности для горно-обогатительных комбинатов с несколькими вариантами переработки и транспортировки.
В работах [17–20] для решения задачи планирования карьерной разработки используются метаэвристические подходы, такие как алгоритм запрещённого поиска, генетический алгоритм, алгоритм летучих мышей, алгоритм стаи серых волков, алгоритм светлячков и алгоритм роя частиц, а полученные результаты сравниваются с классическими методами.
3. Предлагаемый алгоритм улучшения времени решения
Предлагаемый метод направлен на достижение оптимальных или близких к оптимальным решений за более короткое время за счет сужения пространства решения задачи путем стратегического установления переменных решения ЦП-модели задачи планирования карьерной разработки. Процесс принятия решений, используемый для установления переменных решения в данном контексте, основан на вложенных контурах карьера, созданных в результате параметрического анализа конечного контура карьера. Традиционный подход предполагает представление экономической блочной модели месторождения полезных ископаемых в виде сети, основанной на теории графов. Затем эта сеть подвергается анализу с помощью алгоритмов максимального потока, чтобы найти конечный контур карьера, который соответствует объему добычи, приносящему наибольший доход. На следующем этапе блоки в пределах конечного контура карьера подвергаются анализу максимального потока. Этот анализ предполагает пересчет их экономической ценности на основе коэффициента корректировки дохода (RAF), в результате чего границы карьера постепенно сужаются (т. е. контур сокращается). Вышеупомянутые границы соответствуют вложенным контурам карьера.
В описанной выше процедуре подбор RAF заключается в последовательном увеличении его на 0,01, часто в диапазоне от 0,2 до 1, чтобы установить приблизительный расчет для 80 вложенных контуров (границ) карьера. Затем производится расчет количества руды и пустой породы, содержания ценного компонента и экономической ценности, получаемой в результате выемки материала в пределах этих вложенных контуров карьера. После этих вычислений выбираются контуры карьера, обеспечивающие годовую мощность по добыче, для представления долгосрочного плана добычи, а затем проводится определение для решения задачи планирования разработки карьера. Одна из существенных проблем, связанных с этим методом, касается значительного изменения размеров последовательных контуров карьера, которые определяются на основе коэффициента корректировки дохода. При достижении определенного порога эти контуры быстро изменяются в размерах. В результате количество материала, доступного между двумя последовательными контурами, обычно значительно превышает годовую мощность по добыче. В научной литературе эта ситуация известна как проблема разрыва. На рис. 8 представлена численная иллюстрация данной ситуации. Гистограмма, представленная на рис. 7, показывает, что параметрический анализ дает минимальный размер конечного контура карьера в 18 блоков, в то время как ближайший второй по величине контур карьера содержит 3049 блоков. Проблема разрыва связана с отсутствием подходящей границы (контура) карьера, которую можно было бы выбрать на начальный период при использовании традиционного метода планирования.
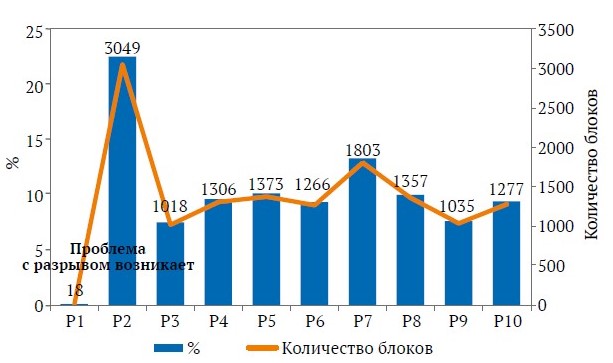
Рис. 7. Проблема разрыва, иллюстрируемая распределением блоков внутри вложенных контуров карьера

Рис. 8. 2D-разрез примеров вложенных контуров карьера (с возможными контурами по периодам)
В данной работе предлагается гибридное решение, сочетающее методологию вложенных контуров карьера с подходом целочисленного (линейного) программирования (IP/ILP) в качестве способа устранения вышеупомянутых проблем. Целью предложенного алгоритма является установление переменных решения модели целочисленного программирования (ЦП) с использованием вложенных конечных контуров (границ) карьера, полученных с помощью параметрического анализа. Акт установления переменных решения в контексте целочисленного программирования означает предопределение определенных переменных решения, которые в конечном итоге диктуют планирование добычи на открытых горных работах в заранее определенных границах. Такой подход дает эффективные результаты за счет уменьшения сложности модели задачи. В следующем разделе описаны этапы предложенного алгоритма.
Алгоритм
1. Использование алгоритма псевдопотока Хохбаума для определения конечного контура карьера.
- Внешний (конечный) контур карьера на рис. 8 (все блоки в пределах внешнего контура карьера, полученного при RAF = 1).
- Формирование вложенных контуров карьера путем использования параметрического анализа блоков, расположенных в пределах конечного контура карьера, с применением RAF (см. рис. 8).
2. Расчет количества материала во вложенных контурах карьера, а также выявление потенциальных контуров карьера, которые могут обеспечить запланированную годовую мощность по добыче (см. рис. 8).
- Внутренний (начальный) контур карьера – это потенциальный контур для первого периода разработки (оранжевые блоки, полученные при RAF = 0,2). Второй контур карьера – это потенциальный контур для второго периода разработки (зеленые блоки, полученные при RAF = 0,4).
3. В каждый период времени фиксируются переменные решения блоков, расположенных за пределами вложенного контура карьера, который был определен как потенциальный контур на этот конкретный период (рис. 9, 10).
- Например, для T = 4 периода переменные xi1 серых блоков устанавливаются как 0, так как оранжевые блоки представляют потенциальный контур карьера для 1-го периода и приносят наибольший доход при достаточном количестве руды внутри них (см. рис. 9). Другой пример можно увидеть на рис. 10. Переменные xi2 серых блоков зафиксированы как 0, поэтому блоки, которые будут извлечены во время второго периода добычи, будут искаться в пределах зеленой границы (контура), поскольку руд достаточно для перерабатывающих мощностей, и они приносят наибольший доход.
4. Для установления переменных в контексте обилия руды в потенциальном контуре за определенный период времени применяется другая стратегия. В этой процедуре, если в контуре имеется избыточное количество руды, переменные решения для блоков в этом контуре устанавливаются как 1, так как ожидается, что эти блоки будут извлечены в последующие периоды, т.е. переменные xi5, связанные с розовыми блоками на рис. 11, фиксируются как 1 – это означает, что ожидается, что они будут извлечены в конце T = 5).
5. Окончательный процесс установления переменных осуществляется следующим образом: если количество руды в потенциальном контуре меньше, чем мощность по добыче руды, переменная решения для всех блоков в этом контуре устанавливается как 1, так как эти блоки могут быть извлечены в течение этого периода времени (синие блоки на рис. 11).
6. Решение задачи с уменьшенным размером, который получается при установлении переменных решения.
Блочные модели, приведенные в табл. 1, были получены из MineLib – набора данных, широко используемого в горнодобывающей промышленности.
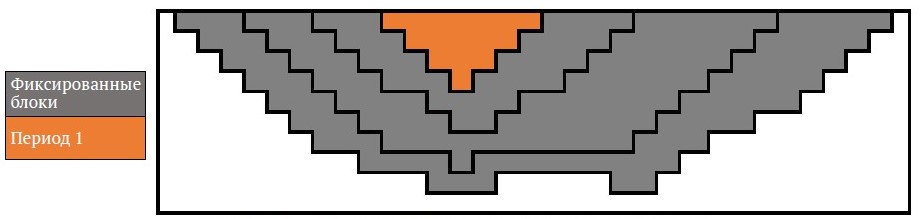
Рис. 9. Пример установления переменных для 1-го периода
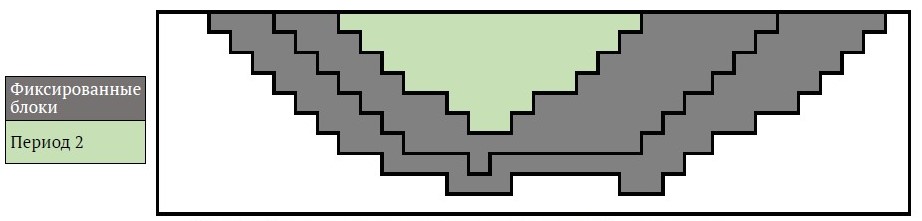
Рис. 10. Пример установления переменных для 2-го периода
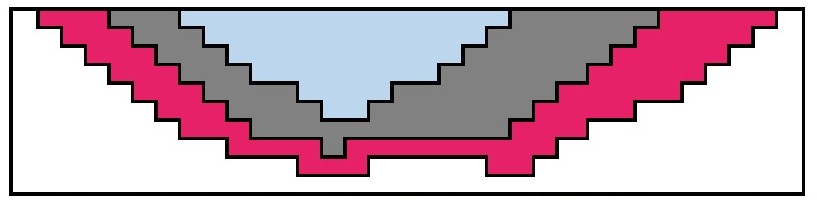
Рис. 11. Установление переменных в контексте обилия руды (розовые блоки) и недостатка руды (синие блоки)
Таблица 1
Характеристики блочной модели
| Блочная модель (алгоритм) | Количество блоков | Количество блоков в пределах конечного контура карьера | Количество двоичных переменных | Мощность добычи по руде, т | Учётная ставка | Периоды времени T |
| zuck_small | 9400 | 8752 | 122 528 | 20 млн | 10 % | 14 |
| kd | 14 153 | 13 258 | 132 580 | 10 млн | 10 % | 10 |
| zuck_medium | 29 277 | 29 230 | 263 880 | 8 млн | 10 % | 9 |
| marvin | 53 271 | 5324 | 69 212 | 20 млн | 10 % | 13 |
| zuck_large | 96 821 | 96 821 | 968 210 | 3 млн | 10 % | 10 |
| mclaughlin | 2 140 342 | 112 687 | 1 126 687 | 3,5 млн | 10 % | 10 |
4. Численные результаты, полученные предложенным методом
Предложенная методика сокращения времени решения задачи планирования карьерной разработки реализована на шести различных блочных моделях, полученных из MineLib. MineLib включает различные примеры блочных моделей, используемые для демонстрации работы различных алгоритмов, предлагаемых для решения задачи планирования карьерной разработки. Результаты представлены следующим образом. Сначала решения и результаты для блочных моделей пытались получить без установления переменных решения. После этого предложенный нами метод применялся к той же блочной модели, и исследовалось сокращение времени решения. Для решения ЦП-моделей используется решатель GUROBI. Релаксация разрыва оптимальности установлена как %1, а верхняя граница времени работы – на уровне 36000 с. Решатель GUROBI использует метод барьеров для определения верхней границы ЦП релаксации. В табл. 2 приведены численные результаты предложенного метода и его сравнение со стандартной ЦП-моделью. Аббревиатура «Nstl» означает отсутствие решения в заданный срок, а «memory» – ситуацию, когда методика вычислений для решения модели не поддерживается доступным объемом памяти компьютера (т.е. ситуацию ограниченности вычислительных ресурсов). «%inf» означает, что уменьшение времени решения не удалось измерить, поскольку стандартная ЦП-модель не смогла решить задачу в заданный срок или превышала возможности (объем) оперативной памяти компьютера.
Как видно из табл. 2, применяя предложенную методику к различным блочным моделям, мы смогли заметить значительное улучшение в продолжительности времени решения (т.е. сокращение этого времени). Это демонстрирует эффективность и практичность предложенного метода в реальных условиях. В то же время некоторые проблемы, которые не могут быть решены с помощью общей ЦП-модели, были решены с помощью предложенного метода, что свидетельствует об эффективности предложенного метода. При расчете ЧПС решения наблюдается некоторое снижение величины ЧПС, что является недостатком предложенной методики. Такая ситуация возникает из-за ограничения альтернативных вариантов решения с вложенными контурами (границами) карьера. Снижение чистой приведенной стоимости (ЧПС) может считаться приемлемым в контексте решения сложных блочных моделей значительного масштаба, решение которых является невыполнимым (традиционными способами). Дополнительным ограничением предложенного алгоритма является его зависимость от наличия ограничений на мощность по добыче руды. Решения, полученные с помощью этой методики, могут оказаться невыполнимыми при наличии ограничений на общую мощность по добыче руды. Для устранения этого ограничения одним из возможных решений является включение методов релаксации в модель целочисленного программирования (ЦП-модель). Это позволит включить ограничения на общую мощность по добыче руды в целевую функцию с помощью множителей Лагранжа. Кроме того, можно использовать различные эвристические подходы для обеспечения соблюдения ограничений на общую мощность по добыче руды после решения модели целочисленного программирования (ЦП) с использованием предложенной стратегии.
Таблица 2
Численные результаты
| Блочная модель (алгоритм) | Время решения стандартной ЦЛП-модели, с | ЧПС стандартной ЦЛП-модели | Разрыв оптимальности | Время решения предложенного алгоритма, с | ЧПС предложенного алгоритма | Разрыв оптимальности | Сокращение времени решения |
| zuck_small | 2 688 | 827,4 млн | 1,79 % | 110 | 815,2 млн | 0,60 % | –95 % |
| kd | 2 806 | 413,2 млн | 0,15 % | 177 | 405,7 млн | 0,98 % | –93 % |
| zuck_medium | 23 110 | 721,3 млн | 1,7 % | 428 | 706,3 млн | 0,88 % | –98 % |
| marvin | 1 471 | 799,5 млн | 0,98 % | 71 | 798,3 млн | 0,96 % | –95 % |
| zuck_large | Nstl | Nstl | Nstl | 2 221 | 76,9 млн | 0,08 % | %inf |
| mclaughlin | Memory | Memory | Memory | 3 332 | 1 031,2 млн | 0,16 % | %inf |
Графические результаты блочной модели Марвина (Marvin) представлены на рис. 12, что позволяет сравнить предложенную методологию с традиционной ЦП-моделью. Очевидно, что аналогичные результаты могут быть достигнуты в более короткие сроки за счет установления (фиксирования) переменных. Результаты работы предложенного алгоритма дополнительно сравниваются с результатами, достигнутыми модифицированным алгоритмом TopoSort (Топосорт) в [11] и алгоритмом Bienstock & Zuckerberg (Бьенстока-Цукерберга) в [21], как показано в табл. 3. Результаты алгоритма TopoSort являются оптимальными и наиболее выполнимыми из известных результатов соответствующих блочных моделей. Алгоритм, предложенный Бьенстоком и Цукербергом, дает лучшую чистую приведенную стоимость (ЧПС); тем не менее эти результаты считаются невыполнимыми.
Судя по результатам, представленным в табл. 3, предложенная методология демонстрирует заметную эффективность в решении задачи планирования карьерной разработки, а также потенциал для повышения максимально достижимой ЧПС для определенных блочных моделей, как указывается в MineLib [22].
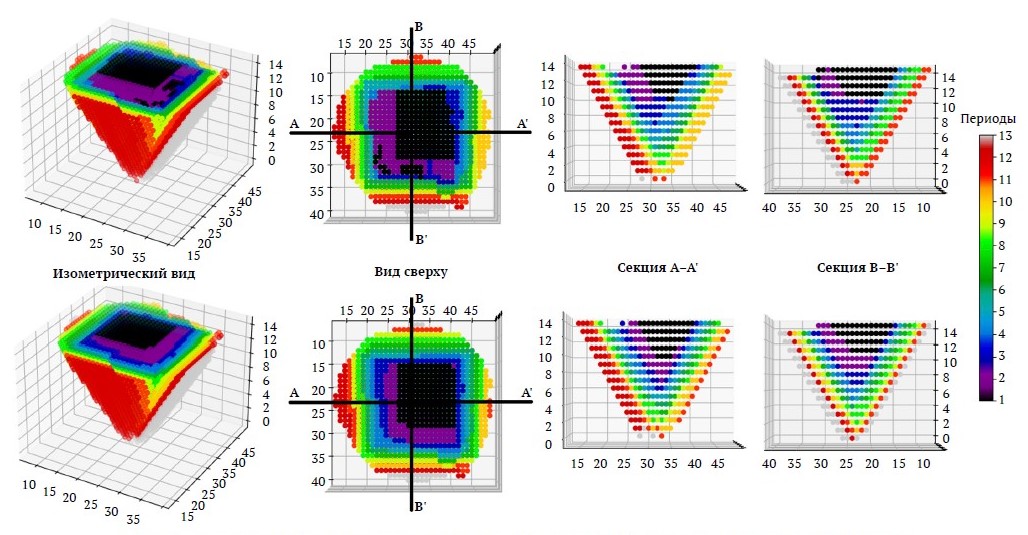
Рис. 12. Пример сравнения результатов планирования для блочной модели Марвина (Marvin) (результат обычной ЦП-модели (вверху), результат ЦП-модели с установленными переменными решения (внизу))
Таблица 3
Сравнение ЧПС предлагаемого алгоритма с другими исследованиями в данной области
| Блочная модель | TopoSort | Bienstock & Zuckerberg | Предлагаемый алгоритм |
| mclaughlin | 1073,3 млн | 1079,0 млн | 1031,2 млн |
| marvin | 820,7 млн | 863,4 млн | 798,3 млн |
| zuck_medium | 615,4 млн | 710,6 млн | 706,3 млн |
| kd | 396,8 млн | 409,4 млн | 405,7 млн |
| zuck_small | 788,6 млн | 854,2 млн | 815,2 млн |
Заключение и предложения по дальнейшим исследованиям
Открытые горные работы играют важную роль в социально-экономическом развитии стран и горных технологий, поскольку обеспечивают добычу ценных полезных ископаемых, которые необходимы для этого развития. Достижение рентабельности горных работ требует применения подхода, основанного на стратегическом планировании. В этом конкретном контексте многие исследователи предложили альтернативные подходы к решению проблемы планирования добычи полезных ископаемых открытым способом. Основная цель этой процедуры планирования – максимизация чистой приведенной стоимости. Методы, представленные в этой области, включают в себя алгоритмы максимального потока, линейное программирование, целочисленное программирование, динамическое программирование, метаэвристические методы и методы моделирования. Хотя эти стратегии доказали свою эффективность при работе с небольшими и средними по объему запасов рудными месторождениями, их действенность и эффективность ограничены, когда речь идет о крупных месторождениях полезных ископаемых. В данной работе представлен рекомендуемый альтернативный подход, направленный на преодоление проблем, связанных с реализацией существующих подходов в контексте крупных месторождениий полезных ископаемых. Традиционно задача планирования карьерной разработки решается путем ручного выбора из вложенных контуров (границ) карьера, полученных в результате параметрического анализа месторождения полезных ископаемых, тех, которые соответствуют годовой мощности по добыче руды. Целью данного исследования является уменьшение объема задачи путем ограничения некоторых переменных решения модели целочисленного программирования с помощью пределов (ограничений), полученных из традиционных подходов. Этот подход направлен на решение задач, связанных с блочными моделями месторождений полезных ископаемых, которые либо неразрешимы, либо требуют чрезмерного времени для решения в ограниченные сроки. Эффективность предложенного метода была продемонстрирована в ходе его применения к блочным моделям-образцам из современных литературных источников. Полученные результаты показывают, что предложенный метод не только значительно сокращает время решения, на величину до 95 %, но и позволяет решать модели, которые ранее были неразрешимы из-за ограниченности вычислительных ресурсов. Хотя снижение ЧПС для некоторых моделей может показаться недостатком этого метода, он является значительным вкладом в горнодобывающую промышленность, поскольку за короткий период времени можно рассмотреть различные альтернативные варианты планов-графиков по добыче руд, исходя из изменяющихся мощностей по добыче и цен реализации руды.
Потенциал дальнейших исследований включает в себя включение в процедуру планирования таких параметров, как содержания ценных компонентов в рудах, вертикальная скорость разработки и минимальная ширина разработки, которые должны учитываться при проведении горных работ. Учет эксплуатационных факторов, таких как минимальная ширина разработки, может быть достигнут путем включения их в качестве соответствующих ограничений на этапе параметрического анализа предлагаемого метода. При таком подходе перед решением модели целочисленного программирования (ЦП) потенциальные контуры карьера для периодов должны будут удовлетворять заданным ограничениям. Кроме того, дальнейшие исследования могли бы изучить влияние методов, используемых для обеспечения соответствия ограничениям, определяемым общей мощностью по добыче. Кроме того, стоит рассмотреть возможность применения метаэвристических подходов в качестве потенциальных направлений будущих исследований. Эти методы, хотя и сложны для разработки жизнеспособного плана добычи на начальном этапе, могут быть применены в дальнейших исследованиях, где используются первоначальные результаты, полученные с помощью предложенного метода, а чистая приведенная стоимость (ЧПС) повышается за счет применения различных метаэвристических методов, таких как метод моделирования отжига, алгоритм запрещённого поиска и муравьиный алгоритм оптимизации.
Список литературы
1. Caccetta L., Hill S. An application of branch and cut to open pit mine scheduling. Journal of Global Optimization. 2003;27:349–365. https://doi.org/10.1023/A:1024835022186
2. Lerchs H., Grossmann I. F. Optimum design of open-pit mines. Transactions, C.I.M. 1965;LXVIII:17–24.
3. Dagdelen K., Johnson T. B. Optimum open-pit mine production scheduling by Lagrangian parameterization. In: Proceedings of the 19th APCOM. 1984;127–142.
4. Elkington T., Durham R. Integrated open pit pushback selection and production capacity optimization. Journal of Mining Science. 2011;47:177–190. https://doi.org/10.1134/S1062739147020055
5. Kumral M. Production planning of mines: optimization of block sequencing and destination. International Journal of Mining, Reclamation, and Environment. 2012;26(2):93–103. https://doi.org/10.1080/17480930.2011.644474
6. Jélvez E., Morales N., Askari-Nasab H. A new model for automated pushback selection. Computers & Operations Research. 2020;115:104456. https://doi.org/10.1016/j.cor.2018.04.015
7. Tolwinski B., Underwood R. An algorithm to estimate the optimal evaluation of an open-pit mine. In: Proceedings of the 23rd International Symposium on the Application of Computers and Operations Research in the Mineral Industries. 1992;399–409.
8. Picard J. C. Maximal closure of a graph and applications to combinatorial problems. Management Science. 1976;22(11):1268–1272. https://doi.org/10.1287/mnsc.22.11.1268
9. Tachefine B., Soumis F. Maximal closure on a graph with resource constraints. Computers & Operations Research. 1997;24(10):981–990. https://doi.org/10.1016/S0305-0548(97)00008-7
10. Chandran B. G., Hochbaum D. S. A computational study of the pseudoflow and push-relabel algorithms for the maximum flow problem. Operations Research. 2009;57(2):358–376. https://doi.org/10.1287/opre.1080.0572
11. Hochbaum D. S. The pseudoflow algorithm: A new algorithm for the maximum-flow problem Operations Research. 2008;56(4):992–1009. https://doi.org/10.1287/opre.1080.0524
12. Hochbaum D. S., Chen A. Performance analysis and best implementations of old and new algorithms for the open- pit mining problem. Operations Research. 2000;48(6):894–914. https://doi.org/10.1287/opre.48.6.894.12392
13. Muoz G., Espinoza D., Goycoolea M. et al. A study of the Bienstock-Zuckerberg algorithm: applications in mining and resource-constrained project scheduling. Computational Optimization and Applications. 2018;69(2):501–534. https://doi.org/10.1007/s10589-017-9946-1
14. Paithankar A., Chatterjee S. Open-pit mine production schedule optimization using a hybrid of maximum-flow and genetic algorithms. Applied Soft Computing. 2019;81:105507. https://doi.org/10.1016/j.asoc.2019.105507
15. Ramazan S., Dimitrakopoulos R. Stochastic optimisation of long-term production scheduling for open pit mines with a new integer programming formulation. İn: Dimitrakopoulos R. (ed.) Advances in Applied Strategic Mine Planning. Springer, Cham; 2018. Pp. 139–153. https://doi.org/10.1007/978-3-319-69320-0_11
16. Montiel L., Dimitrakopoulos R. Optimizing mining complexes with multiple processing and transportation alternatives: An uncertainty-based approach. European Journal of Operational Research. 2015;247(1):166–178. https://doi.org/10.1016/j.ejor.2015.05.002
17. Alipour A., Khodaiari A. A., Jafari A., Tavakkoli-Moghaddam R. Production scheduling of open-pit mines using genetic algorithms: a case study. International Journal of Management Science and Engineering Management. 2020;15(3):176–183. https://doi.org/10.1080/17509653.2019.1683090
18. Elsayed S., Sarker R., Essam D., Coello C. C. Evolutionary approach for large-scale mine scheduling. Information Sciences. 2020;523:77–90. https://doi.org/10.1016/j.ins.2020.02.074
19. Senécal R., Dimitrakopoulos R. Long-term mine production scheduling with multiple processing destinations under mineral supply uncertainty, based on a multi-neighborhood Tabu search. International Journal of Mining, Reclamation, and Environment. 2020;34(7):459–475. https://doi.org/10.1080/17480930.2019.1595902
20. Tolouei K., Moosavi E., Tabrizi A. H. B. et al. Improving performance of open-pit mine production scheduling problems under grade uncertainty by hybrid algorithms. Journal of Central South University. 2020;27(9):2479–2493. https://doi.org/10.1007/s11771-020-4474-z
21. Bienstock D., Zuckerberg M. Solving L. P. relaxations of large-scale precedence constrained problems. In: Eisenbrand F., Shepherd F. B. (eds.) Integer Programming and Combinatorial Optimization. IPCO 2010. Lecture Notes in Computer Science. Vol. 6080. Springer, Berlin, Heidelberg; 2010. https://doi.org/10.1007/978-3-642-13036-6_1
22. Espinoza D., Goycoolea M., Moreno E., Newman A. N. MineLib: a library of open pit problems. Annals of Operations Research. 2013;206:93–114. https://doi.org/10.1007/s10479-012-1258-3
Об авторах
К. ХасоздемирТурция
Курсат Хасоздемир – аспирант, cтажер-исследователь, факультет горного дела
г. Стамбул
С. Г. Эрчелеби
Турция
Селамет Гюрбюз Эрчелеби – доктор наук, профессор, факультет горного дела
г. Стамбул
Рецензия
Для цитирования:
Хасоздемир К., Эрчелеби С. Повышение эффективности целочисленных моделей для решения задачи долгосрочного планирования добычи на открытых горных работах путем установления переменных решений на основе параметрического анализа конечного контура карьера. Горные науки и технологии. 2024;9(2):74-84. https://doi.org/10.17073/2500-0632-2023-09-156
For citation:
Hasozdemir K., Erçelebi S. Enhancing the performance of integer models for addressing the long-term production planning problem in open pit mines by decision variable fixation based on parametric analysis of the final pit limit. Mining Science and Technology (Russia). 2024;9(2):74-84. https://doi.org/10.17073/2500-0632-2023-09-156




































