Scroll to:
Theoretical aspects of block stone blasting method
https://doi.org/10.17073/2500-0632-2023-12-187
Abstract
Block stone excavation is a key aspect of the building materials industry, important for providing construction with durable materials and when giving aesthetic solutions to various structures and design elements. However, when excavating stone (using drilling and blasting), it is necessary to maintain its integrity for further processing and use. The conditions required for applying the method of blasting separation (split off) of stone blocks from hard rock mass were considered, which is important for improving the quality of blasted stone blocks. The rational parameters of stone block blasting with Granilen elastic tubular charges (Granilen ETCs) are presented. An approach to the preliminary assessment of stone block fracturing zone under various explosive loading regimes was determined. The relationship between the consumption of explosives and fracturing of stone blocks at possible blasthole spacing was considered. The mechanism of creating an extended rupture plane in a rock mass was studied. The decisive role of stress waves in the formation of an extended main rupture along the line of blasthole charges was established. It was shown that it is possible to localize the zone of induced fracturing by regulating the conditions for the interaction of stress waves. The results of numerical modeling of stress fields at blasting a single charge and a two-charge Granilen ETC system are presented, which made it possible to assess zones of induced fracturing and the conditionsfor the formation of a main rupture. Blasting effectiveness increases significantly due to the orientation of the expected stone block separation line parallel to the plane of the best rupture, taking into account the anisotropy of the physical and mechanical properties of granites. The study confirms the feasibility of increasing the yield of commodity blocks when selecting rational blasting parameters.
Keywords
For citations:
Kovalevsky V.N., Mysin A.V., Sushkova V.I. Theoretical aspects of block stone blasting method. Mining Science and Technology (Russia). 2024;9(2):97-104. https://doi.org/10.17073/2500-0632-2023-12-187
Theoretical aspects of block stone blasting method
Introduction
Block stone excavation is a key aspect of the building materials industry, important for providing construction with durable materials and when giving aesthetic solutions to various structures and design elements. However, when excavating stone (using drilling and blasting), it is necessary to maintain its integrity for further processing and use [1].
Some deposits demonstrate high variability in physical and mechanical properties in different parts of a quarry field.
The natural features of natural stone deposits determine the volume of blocks mined and their yield from a rock mas being developed [2]. They are governed by the distances between existing fractures, which vary widely in granite rock masses [3].
The choice of a block stone blasting process flow sheet (PFS) is determined by the structure of rock mass, petrographic features, geometric dimensions of the useful thickness [4].
In this regard, drilling and blasting method in the development of block stone deposits remains in demand at present [5].
As studies [6-8] show, the main parameters of drilling and blasting operations at separation of stone blocks from a rock mass are a blasthole diameter, distance between blastholes, their depth, thickness of a separated stone block, charge type, design, mass, diameter.
The choice of the optimal blasthole spacing depends both on the physical and mechanical properties of a rock and on the initial parameters of the blast pulse: the amplitude of the initial pressure in the blast chamber and the duration of action at the quasi-static stage, necessary for the formation and growth of the main rupture between the blastholes, as well as to ensure the movement of a stone block [9].
In this case, the blasting conditions should ensure the creation of a fracture in the split-off plane with minimal disturbance of the peri-blasthole space [10].
In order to ensure the process of directional fracturing, it is necessary that the pressure of blast products would be greater than the tensile strength of a rock, and, for the preservation of a peripheral rock mass, the pressure of blast products in a blasthole should not exceed the rock compressive strength [11]. These conditions are achieved by selecting rational blasthole spacing and optimal parameters of a blast pulse [12, 13]. In particular, the use of Granilen ETCs fully allows meeting these requirements [14].
Performing directed fracturing is possible when the pressure of gaseous products in a blasthole exceeds the dynamic tensile strength of a rock, and the preservation of a rock mass in the peri-blasthole zone requires that this pressure does not exceed the compressive strength of the rock [15–17].
The results of the studies presented in [18–19] indicate that the increase of the radial air gap with respect to the radius of the charge by 3-4 times provides a predominant role of the blast products quasi-static pressure in the directional rupturing. Therefore, a very effective way to control the intensity of the wave and quasi-static stress field can be the regulation of the volumetric concentration of explosive charge energy in a blasthole [20].
The use of Granilen ETCs assumes the creation of the above conditions. The design of Granilen ETCs provides the possibility of regulating the force and time parameters of a blast impulse by changing a charge mass in a blasthole, its length, using the gap between the charge and the blasthole wall, applying stemming, varying blasthole spacing.
The substantiated rational values of blasthole charges parameters allow providing the minimum roughness of faces of a split off stone block and insignificant induced fracturing in the peri-blasthole zone.
Methods and materials
As a rule, separation of a stone block from a rock mass occurs when closely spaced blasthole charges are simultaneously initiated with the detonating cord. In this case, the rock in the plane of location of charges in block perimeter blastholes will be subjected mainly to the action of tensile stresses [21–23].
Consequently, the following conditions must be met in order to split off a block and move it by 0.15–0.3 m [24]:
F ≥ F1 + F2 + F3, (1)
where F is force causing breaking away (separation) and displacement of a stone block, Pa; F1 is force leading to split off of a stone block from a rock mass with rupturing area S (S = BHbench), Pa, where B is length of a stone block, m; Hbench is bench height, m; F2 is friction force, Pa; F3 is a force allowing to take into account the layer dip angle, Pa.
Then:
F = PbpNdbhLbh, (2)
where Pbp – is pressure of gaseous blast products in a blasthole, Pa; N is number of blastholes in a row, pcs; dbh is blasthole diameter, m; Lbh is blasthole depth, m;
where σdrupt is dynamic tensile strength, Pa;
σdrupt = KweakKfKi[σdrupt], (4)
where Kweak is a coefficient of structural weakening of a rock mass, Kweak = 0.2–0.4;
Ki is coefficient of impact (for granite = 4–5.7)1; Kf is acoustic index of fracturing; Ср.rm and Ср are P-wave velocities in a rock mass and rock sample, respectively, m / s.
The force which should be applied to overcome the friction between the block and the base as the block moves:
F2 = Ffr = f1G cos α, (5)
where f1 = tg α is friction coefficient; G is rough block of stone weight, kg:
G = ρrmBHbenchW, (6)
where ρrm is density of rock mass, kg/m3; W is line of least resistance, m; F3 is force allowing to account for a layer dip angle, Pa:
F3 = G sin α. (7)
The solution of equations (1)–(7) allows obtaining an expression for calculating the number of blastholes:
The length of a split off block
where а is the distance between blasthole charges, m:
Choosing the type of explosives (in our case, Granilen-2 ETC) and using the Noble-Abel formula [25], we determined the mass of explosive to be blasted in a blasthole volume to create the required pressure of detonation products Рbp (11):
where Т0 is initial temperature, Т0 = 273 К; n is the number of moles of gaseous blast products; Тbl is temperature of blast products, K; К; Р0 is atmospheric pressure, Pa, Р0 = 0,1 МПа.
During blasting separation of a stone block from a rock mass, ruptures and fractures originate in places where pulse reactions occur, the intensity of which is sufficient for rock rupture and which is determined by the charge design, power, and location in the separated stone block [26–28].
In the presence of a layer rupture, the depth of the placed charge (eccentricity) is determined from the following expression:
where Н is height of a rock block, m; W is width (thickness) of a rock block, m.
In case of the absence of a layer rupture, the depth of charge placement is determined from the following expression:
where fd and f′d are dynamic friction coefficients at the top and bottom vertices of a stone block. For approximate calculations, we can assume fd = 0.25; f′d = 0.5.
The optimal width (thickness) of a stone block is determined from the following expression:
where hch is charge height, m; m is underbreak, m.
Based on the above methodology, the parameters of drilling and blasting operations for stone block splitting off using Granilen-2 ETCs were calculated, which are presented in Table 1. Along with the determination of the key D&B parameters, the most important condition for the extraction of high-quality stone blocks is the accuracy of delineation of the separated stone block and ensuring the minimum radius of induced fracturing in the peri-blasthole zone.
Table 1
Design D&B parameters for rock block excavation in the presence of bottom rupture (dbh = 42 mm, dch = 15 mm, lbh =2.9 m)
| Item | Blasthole spacing, m | |||
| 0.3 | 0.4 | 0.5 | 0.6 | |
| Charge weight in a blasthole, kg | 0.27 | 0.36 | 0.45 | 0.54 |
| Total charge weight, kg | 22.4 | 22.7 | 22.5 | 22.7 |
| Number of blastholes | 83 | 63 | 50 | 42 |
| Blasthole pressure, MPa | 31.0 | 42.5 | 55.5 | 67.0 |
| Expected radius of induced fracturing, m | 0.026 | 0.03 | 0.035 | 0.038 |
| Charge length in a blasthole, m | 0.75 | 0.84 | 1.4 | 1.7 |
The values of these block contour deviations are determined by the charge convergence coefficient equal to
where а is blasthole spacing, m; W is width of a stone block, m.
Consequently, the minimum values of a stone block side roughness can be achieved at the optimal value of n.
Based on the results of the tests performed at granite block stone quarries, the dependence of the magnitude of the block contour deviation on blasthole Granilen-2 ETCs spacing was obtained (Fig. 1).
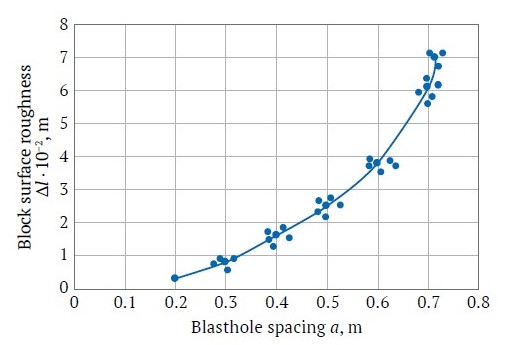
Fig. 1. Block surface roughness as a function of blasthole spacing
At low-velocity loading mode and interaction of stress waves, an asymmetric stress field is formed around the peripheral (contour) blastholes, which leads to deterministic growth of the main rupture in the split off plane.
Since microfractures are generated by a tensile stress pulse, their surfaces coincide with the radial planes. A contour rupture propagates simultaneously along several structural fractures by fusing microfractures into macrofractures [29]. As a consequence, along the line connecting neighboring charges, the rock mass is weakened by tensile stresses along the contour line, and the main rupture starts to grow between the blastholes, while the growth of side fractures is suspended [30–31].
The results of studies [25], [32] show that the radius of the zone of induced fracturing in a split off stone block depends both on the size of the charges in the blastholes and the blasthole spacing. The rupture kinetics at directional rupture is determined by both the physical-and-mechanical properties of rocks and the parameters of stresses and pressures created by the blast products in a charge chamber (blasthole).
When a system of cylindrical charges is blasted, stress waves interact, resulting in a transformation of the stress field.
The approximate method of stress field estimation on the basis of numerical modeling and analytical calculation was used according to the methodology set forth in the studies on the blast of charges with air gap.
As an explosive, Granilen-1 ETCs with charge diameter dch = 11 mm with blast heat Q = 1550 kJ/kg was used. The charges were located in blastholes of diameter dbh = 42 mm in granite rock mass with rock density ρrocks = 2200 kg/m3, with longitudinal wave velocity Сp = 6200 m/s.
The condition of interaction of stress waves providing the main rupture propagation was determined from the expression
where σϕ1 and σϕ2 are amplitudes of tangential component of stress wave from blasts of neighboring charges, respectively; a – charges spacing, m; σ*dynrupt – dynamic tensile strength of granite, Pa.
Then [33],
where σstrupt is static tensile strength, σstrupt = 9,1 MPa, σ*dynrupt = 36,4 MPa.
This value was taken as the ultimate stress level, below which no main rupture propagation occurred.
The length of a natural microfracture l0 for granites according to the data of [33] was 0.01–0.03 cm.
The maximum amplitude pressure on a blasthole walls for granites should not exceed 90 MPa [25].
1Dambaev Zh. G. Physical bases of directional rock blasting and techniques of gentle block stone blasting. [Abstract of Doctoral thesis in Eng. Sci.]. St. Petersburg; 2000. 37 p. (In Russ.)
Findings
Figs. 2–4 show the results of calculation of the maximum tangential tensile stresses field when blasting a system of two Granilen-1 ETCs spaced 0.47 and 0.58 m. The charges were initiated simultaneously using a DShE-12 detonating cord passing through the charge channel. The linear densities of charge were 0.14 and 0.16 kg/m.
It follows from the results that the interaction of simultaneously blasted charges leads to a significant change in the stress field in the vicinity of the plane passing through the charges.
It is obvious that if for a single charge the stress continuously decreases with growing distance from the charge, then for interacting charges the stress initially (at first) decreases with growing distance from the charges, and then increases again, reaching a maximum at half the distance between the charges. Fig. 5 shows the calculated dependence of individual tangential tensile stresses at linear charging densities q = 0.14 and 0.16 kg/m and charge spacing a = 0.6 m on the distance from a charge.
The data shown in Fig. 5 allow estimating potential zones of induced fracturing around the blasthole.
The given dependencies allow estimating potential zones of induced fracturing around a blasthole at different charging densities.
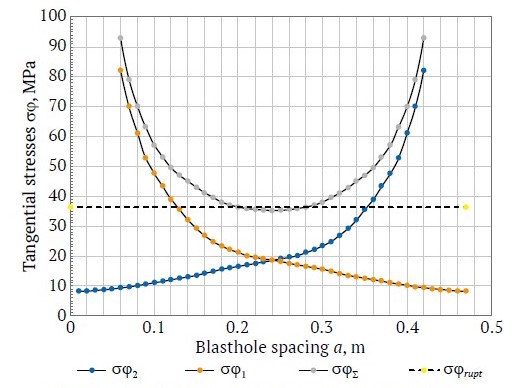
Fig. 2. Individual and total tangential stresses when blasting adjacent charges (a = 0.47 m, q = 0.14 kg/m): σϕ1 and σϕ2 are the amplitudes of the tangential component of the stress wave from the first and second charges, respectively, MPa; σϕΣ is total amplitude of the tangential component of the stress wave from two charges, MPa; σrupt is maximum permissible value of rupture stress, MPa
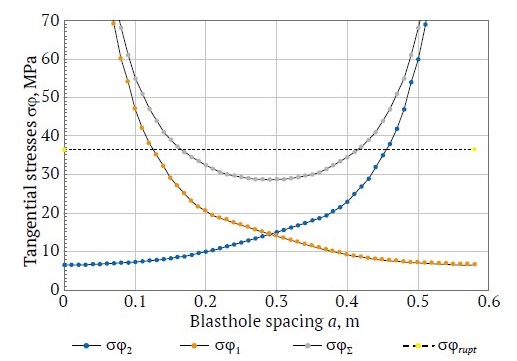
Fig. 3. Individual and total tangential stresses when blasting adjacent charges (a = 0.58 m, q = 0.14 kg / m): σϕ1 and σϕ2 are the amplitudes of the tangential component of the stress wave from the first and second charges, respectively, MPa; σϕΣ is total amplitude of the tangential component of the stress wave from two charges, MPa; σrupt is maximum permissible value of rupture stress, MPa
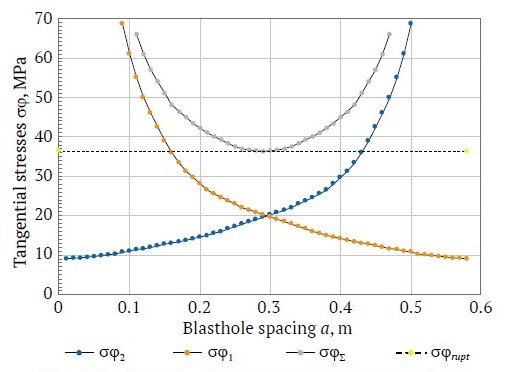
Fig. 4. Individual and total tangential stresses when blasting adjacent charges (a = 0.58 m, q = 0.16 kg/m): σϕ1 and σϕ2 are the amplitudes of the tangential component of the stress wave from the first and second charges, respectively, MPa; σϕΣ is total amplitude of the tangential component of the stress wave from two charges, MPa; σϕrupt is maximum permissible value of rupture stress, MPa
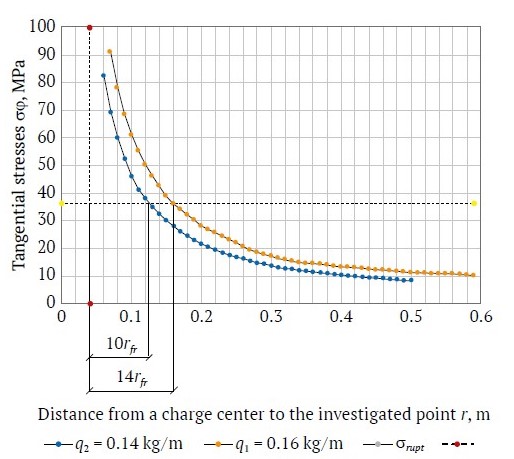
Fig. 5. Zone of induced fracturing at linear charge densities q1 = 0.14 kg/m, q2 = 0.16 kg/m: rfr is radius of fracturing, m; σrupt is maximum permissible value of rupture stress, MP
Conclusion
It was established that for the most probable propagation of radial main rupture between blasthole charges during stone block mining it is necessary to use the effect of stress wave interaction.
It should be noted that in order to minimize the zone of induced fracturing, the charge amount should be selected so that the tensile stress field in the plane of the rupture does not exceed the tensile strength. The main rupture propagation begins with the arrival of a rarefaction wave reflected from the surface of the separated stone block.
It can also be stated that as the average pressure Рavr increases, the length of the main rupture decreases due to the increase in the number of microfractures. Even at the maximum pressure on the blasthole walls, the length of the rupture from an individual blasthole is such that, taking into account the increasing stress intensity factor and the linear system of fractures propagating between blastholes, the blastholes spacing can be much greater than commonly accepted.
However, at low pressure (small number of fractures), this potential blasthole spacing is not feasible due to the random direction of fracture propagation and hence unpredictability of the rupturing (split off) direction. It is therefore necessary to increase the charge (capacity, blasthole pressure) to increase the number of fractures so that the fractures necessarily propagate along or near the direction of the blasthole line.
With the simultaneous growth of the charge size, the blasthole spacing should be reduced so that the growth of fractures propagating from the blastholes in all directions stops early enough (which happens as soon as the fractures growing in the direction of the blasthole line start to “feel each other”) and the disturbed area around the blastholes is minimized.
Thus, obtaining a directional rupture requires reducing the blasthole spacing and at the same time increasing the blasthole charge within certain limits.
The potential for directional rupture at increased blasthole spacing with reduced charges can be realized by using potential naturally occurring directions / weakeness planes) in a stone (cleavage, layering, etc.), which prevent fracture growth in other directions.
References
1. Careddu N. Dimension stones in the circular economy world. Resources Policy. 2019;60:243–245. https://doi.org/10.1016/j.resourpol.2019.01.012
2. Paramonov G. P., Kovalevskyi V. N., Mysin A. V. Determination of the conditions of an effective functioning of elongated cumulative charges in processing the marble stone. Key Engineering Materials. 2020;836:19–24. https://doi.org/10.4028/www.scientific.net/kem.836.19
3. Borovikov V. A., Vanyagin I. F. About calculation of parameters of stress waves when blasting an elongated charge in rocks. Vzryvnoe Delo. 1976;(76/38):74–85. (In Russ.)
4. Skublov S. G., Petrov D. A., Galankina O. L. et al. Th-rich zircon from a pegmatite vein hosted in the Wiborg Rapakivi Granite Massif. Geosciences. 2023;13(12):362. https://doi.org/10.3390/geosciences13120362
5. Isheisky V. A., Ryadinskii D. E., Magomedov G. S. Increasing the quality of fragmentation of blasting rock mass ased on accounting for structural features of massif in the blast design. Mining Informational and Analytical Bulletin. 2023;(9–1):79–95. (In Russ.) https://doi.org/10.25018/0236_1493_2023_91_0_79
6. Kovalev A. V. Ways of improving blasting methods of dimensional stone quarrying in intensively fractured rock mass. Mining Science and Technology (Russia). 2018;(1):23–34. (In Russ.) https://doi.org/10.17073/2500-0632-2018-1-23-34
7. Pal Roy P. Emerging trends in drilling and blasting technology: concerns and commitments. Arabian Journal of Geosciences. 2021;14:652. https://doi.org/10.1007/s12517-021-06949-z
8. Sanchidrián J. A., García-Bermudez P., Jimeno C. L. Optimization of granite splitting by blasting using notched holes. International Journal for Blasting and Fragmentation. 2000;4(1):1–11. https://doi.org/10.1080/13855140009408059
9. Gospodarikov A. P., Revin I. E., Morozov K. V. Composite model of seismic monitoring data analysis during mining operations on the example of the Kukisvumchorrskoye deposit of AO Apatit. Journal of Mining Institute. 2023;262:571–580. https://doi.org/10.31897/PMI.2023.9
10. Барон Л. И., Турчанинов H. A., Ключников A. B. Нарушенность пород при контурном взрывании. Л.: Наука; 1975. 339 с.
11. Боровиков В. А., Ванягин И. Ф. Техника и технология взрывных работ. Л.: Изд-во ЛГИ; 1985. 92 с.
12. Зырянов И. В., Бондаренко И. Ф., Ковалевич С. В., Ким С. И. Влияние взрыва скважинного заряда с радиальным зазором на качество разрушения алмазоносной руды. Горный информационно-аналитический бюллетень. 2022;(5–2):58–71. https://doi.org/10.25018/0236_1493_2022_52_0_58
13. Маринин М. А., Евграфов М. В., Должиков В. В. Производство взрывных работ на заданный гранулометрический состав руды в рамках концепции «mine-to-mill»: современное состояние и перспективы. Известия Томского политехнического университета. Инжиниринг георесурсов. 2021;332(7):65–74. https://doi.org/10.18799/24131830/2021/7/3264
14. Saadati M., Forquin P., Weddfelt K. et al. On the mechanical behavior of granite material with particular emphasis on the influence from pre-existing cracks and defects. Journal of Testing and Evaluation. 2018;46:33–45. https://doi.org/10.1520/JTE20160072
15. Zhang Z. X., Chi L. Y., Qiao Y. Fracture initiation, gas ejection, and strain waves measured on specimen surfaces in model rock blasting. Rock Mechanics and Rock Engineering. 2021;54:647–663. https://doi.org/10.1007/s00603-020-02300-2
16. Borowski G., Smirnov Yu., Ivanov A., Danilov A. Effectiveness of carboxymethyl cellulose solutions for dust suppression in the mining industry. International Journal of Coal Preparation and Utilization. 2020;42(8):2345–2356. https://doi.org/10.1080/19392699.2020.1841177
17. Cardu M., Saltarin S., Todaro C., Deangeli C. Precision rock excavation: beyond controlled blasting and line drilling. Mining. 2021;1(2):192–210. https://doi.org/10.3390/mining1020013
18. Leschinsky A. V., Shevkun E. B., Lysak Yu. A. Control of iron ore fragmentation by blasting-way of improvement of processing efficiency. Mining Informational and Analytical Bulletin. 2019;(4):41–52. (In Russ.) https://doi.org/10.25018/0236-1493-2019-04-0-41-52
19. Darbinyan T. P., Tsymbalov A. A., Zubov V. P., Kolganov A. V. Impact of rock mass jointing on dilution of disseminated copper–nickel ore in Oktyabrsky Mine. Gornyi Zhurnal. 2023;(6):19–26. (In Russ.) https://doi.org/10.17580/gzh.2023.06.03
20. Moldovan D. V., Chernobay V. I., Yastrebova K. N. The influence of composite material in the stemming design on its operability. Mining Informational and Analytical Bulletin. 2023;(9–1):110–121. (In Russ.) https://doi.org/10.25018/0236_1493_2023_91_0_110
21. Protosenya A. G., Belyakov N. A., Bouslova M. A. Modelling of the stress-strain state of block rock mass of ore deposits during development by caving mining systems. Journal of Mining Institute. 2023;262:619–627. URL: https://pmi.spmi.ru/pmi/article/view/15942
22. Rajaoalison H., Zlotkowski A., Rambolamanana G. Mechanical properties of sandstone using non-destructive method. Journal of Mining Institute. 2020;241:113–117. https://doi.org/10.31897/pmi.2020.1.113
23. Panasyuk V. В. Limit equilibrium of brittle bodies with fractures. Kyiv: Naukova Dumka; 1991. 411 p. (In Russ.)
24. Bychkov G. V., Kokunina L. V., Kazakov S. V. Drilling and blasting method of mining of monoliths and natural stone blocks. Gornyi Zhurnal. 2008;(1):45–49. (In Russ.)
25. Blair D. P. Dynamic response of mine pit walls. International Journal of Rock Mechanics and Mining Sciences. 2018;106:14–19. https://doi.org/10.1016/j.ijrmms.2018.04.002
26. Zubov V. P., Li Yunpeng. Slicing mining of thick gently dipping coal in China: Problems and improvement. Mining Informational and Analytical Bulletin. 2023;(7):37–51. (In Russ.) https://doi.org/10.25018/0236_1493_2023_7_0_37
27. Kongar-Syuryun Ch. B., Kovalski E. R. Hardening backfill at potash mines: promising materials regulating stress-strain behavior of rock mass. Geology and Geophysics of Russian South. 2023;13(4):177-187. https://doi.org/10.46698/VNC.2023.34.99.014
28. Efremov E. I., Kravtsov V. S., Myachina N. N. et al. Fundamentals of the theory and methods of explosive crushing of rocks. Kyiv: Naukova Dumka; 1979. 224 p. (In Russ.)
29. Alenichev I. A., Rakhmanov R. A. Empirical regularities investigation of rock mass discharge by explosion on the free surface of a pit bench. Journal of Mining Institute. 2021;249:334–341. https://doi.org/10.31897/PMI.2021.3.2
30. Elkarmoty M., Colla C., Gabrielli E. et al. A combination of GPR survey and laboratory rock tests for evaluating an ornamental stone deposit in a quarry bench. Procedia Engineering. 2017;191:999–1007. https://doi.org/10.1016/j.proeng.2017.05.272
31. Nefedov M. A. Directed destruction of rocks by explosion. St. Petersburg: St. Petersburg University Publ. House; 1991. 188 p.
32. Meshkov A. A., Afanasyev P. I. Physical foundations of explosive destruction of rocks. Monograph. Moscow: Gornaya Kniga; 2021. 124 p.
33. Chertkov V. Ya. Theoretical evaluation of increased microfracturing at block stone blasting. Fiziko- Tekhnicheskie Problemy Pererabotki Poleznykh Iskopaemykh. 1983;(1):36–43 (In Russ.)
About the Authors
V. N. KovalevskyRussian Federation
Vladimir N. Kovalevskiy – Cand. Sci. (Eng.), Associate Professor, Department of Explosive Engineering
Scopus ID 57194598687, ResearcherID AAD-5379-2019
Saint Petersburg
A. V. Mysin
Russian Federation
Alexey V. Mysin – Cand. Sci. (Eng.), Senior Lecturer at the Department of Geoecology
Scopus ID 57196262504
Saint Petersburg
V. I. Sushkova
Russian Federation
Veronica I. Sushkova – PhD-Student at the Department of Explosive Engineering
Scopus ID 58121433200
Saint Petersburg
Review
For citations:
Kovalevsky V.N., Mysin A.V., Sushkova V.I. Theoretical aspects of block stone blasting method. Mining Science and Technology (Russia). 2024;9(2):97-104. https://doi.org/10.17073/2500-0632-2023-12-187
JATS XML




































