Перейти к:
Теоретические аспекты технологии взрывной отбойки блочного камня
https://doi.org/10.17073/2500-0632-2023-12-187
Аннотация
Добыча блочного камня является ключевым аспектом индустрии строительных материалов, важным для обеспечения строительства прочными материалами и при придании эстетических решений различным конструкциям и элементам дизайна. Однако при добыче камня (производстве буровзрывных работ) необходимо сохранить его целостность для последующей обработки и использования. В рамках исследования были рассмотрены условия, необходимые для применения технологии взрывной отбойки блочного камня из скальных горных пород, что актуально для повышения качества отбиваемых камнеблоков. Приведены рациональные параметры взрывной отбойки камнеблоков зарядами эластичными трубчатыми (ЗЭТ) «Гранилен». Определен подход к предварительной оценке зоны нарушенности блочного камня при различных режимах взрывного нагружения. Рассмотрена взаимосвязь между расходом взрывчатых веществ (ВВ) и нарушенностью камнеблоков при возможных расстояниях между шпурами. Исследован механизм создания протяженной плоскости разрыва в массиве горных пород. Установлена определяющая роль волн напряжений при формировании протяженной магистральной трещины по линии шпуровых зарядов. Показана возможность локализации зоны наведенной трещиноватости за счет регулирования условий взаимодействия волн напряжений. Приведены результаты численного моделирования полей напряжений при взрыве одиночных и системы из двух зарядов ЗЭТ «Гранилен», что позволило оценить зоны наведенной трещиноватости и условий формирования магистральной трещины отрыва. Эффективность взрывной отбойки значительно возрастает за счет ориентации линии предполагаемого отрыва монолита параллельно плоскости наилучшего раскола, учитывая при этом анизотропию физико-механических свойств гранитов. Исследование подтверждает возможности повышения выхода товарных блоков при подборе рациональных параметров взрывной отбойки.
Ключевые слова
Для цитирования:
Ковалевский В.Н., Мысин А.В., Сушкова В.И. Теоретические аспекты технологии взрывной отбойки блочного камня. Горные науки и технологии. 2024;9(2):97-104. https://doi.org/10.17073/2500-0632-2023-12-187
For citation:
Kovalevsky V.N., Mysin A.V., Sushkova V.I. Theoretical aspects of block stone blasting method. Mining Science and Technology (Russia). 2024;9(2):97-104. https://doi.org/10.17073/2500-0632-2023-12-187
Теоретические аспекты технологии взрывной отбойки блочного камня
Введение
Добыча блочного камня является ключевым аспектом индустрии строительных материалов, важным для обеспечения строительства прочными материалами и при придании эстетических решений различным конструкциям и элементам дизайна. Однако при добыче камня (производстве буровзрывных работ) необходимо сохранить его целостность для последующей обработки и использования [1].
Некоторым месторождениям присуща высокая переменчивость физико-механических свойств на различных участках карьерного поля.
Природными отдельностями месторождений природного камня определяются объемы добываемых блоков и их выход из разрабатываемого массива [2]. Они обусловлены расстояниями между существующими трещинами, которые на гранитных массивах колеблются в широких пределах [3].
Выбор технологической схемы по отбойке монолитов определяется структурой массива, петрографическими особенностями, геометрическими размерами полезной толщины [4].
В связи с чем буровзрывная технология при разработке месторождений блочного камня остается востребованной и в настоящее время [5].
Как показывают исследования [6–8], основными параметрами буровзрывных работ при отделении камнеблоков от массива являются диаметр шпура, расстояние между шпурами, их глубина, мощность отделяемого монолита, тип заряда, его конструкция, масса, диаметр.
Выбор оптимального расстояния между шпурами зависит как от физико-механических свойств породы, так и от начальных параметров импульса взрыва: амплитуды начального давления во взрывной камере и длительности действия на квазистатической стадии, необходимых для формирования и роста магистральной трещины между шпурами, а также для обеспечения подвижки монолита [9].
При этом условия взрывания должны обеспечивать создание трещины в плоскости откола при минимальных нарушениях околошпурового пространства [10].
Для обеспечения процесса направленного трещинообразования необходимо, чтобы давление продуктов взрыва было бы больше величины критического растягивающего напряжения горной породы, а для сохранности законтурного массива требуется, чтобы давление продуктов взрыва в шпуре не превышало предела прочности на сжатие [11]. Эти условия достигаются выбором рационального расстояния между шпурами и оптимальных параметров импульса взрыва [12, 13]. В частности, применение зарядов ЗЭТ «Гранилен» в полной мере позволяет выполнить эти требования [14].
Реализация направленного разрушения возможна при условии, когда давление газообразных продуктов в шпуре превышает величину динамического предела прочности породы на отрыв и сохранность массива в околошпуровой зоне требует непревышения этого давления над пределом прочности пород на сжатие [15–17].
Результаты исследований, представленные в работах [18, 19], свидетельствуют, что увеличение радиального воздушного зазора по отношению к радиусу заряда в 3–4 раза обеспечивает превалирующую роль в направленном разрушении квазистатическому давлению продуктов взрыва. Поэтому весьма эффективным способом управления интенсивностью волнового и квазистатического поля напряжений может служить регулирование объемной концентрации энергии заряда взрывчатых веществ (ВВ) в шпуре [20].
Применение зарядов ЗЭТ «Гранилен» предполагает реализацию вышеизложенных условий. Конструкция зарядов ЗЭТ «Гранилен» предусматривает возможность регулирования силовых и временных
параметров взрывного импульса за счет изменения массы заряда в шпуре, его длины, использования зазора между зарядом и стенкой шпура, применения забойки, варьирования расстояния между шпурами.
Обоснованное рациональное значение параметров шпуровых зарядов позволяет обеспечивать минимальную шероховатость граней отбиваемого монолита и незначительную наведенную трещиноватость в околошпуровой зоне.
Методы и материалы
Как правило, отделение монолита от массива происходит при срабатывании близко расположенных шпуровых зарядов при их инициировании одновременно с помощью детонирующего шнура. В этом случае порода в плоскости расположения зарядов в контурных шпурах будет подвергаться в основном действию растягивающих напряжений [21–23].
Следовательно, для отрыва блока и его перемещения на величину 0,15–0,3 м [24] необходимо выполнение следующих условий:
F ≥ F1 + F2 + F3, (1)
где F – сила, вызывающая отделение и сдвижение монолита, Па; F1 – сила, приводящая к отрыву монолита от массива по площади S (S = BHbench), Па, где B – длина монолита, м; Hbench – высота уступа, м; F2 сила трения, Па; F3 – сила, позволяющая учитывать угол падения пласта, Па.
Тогда
F = PbpNdbhLbh, (2)
где Pbp – давление газообразных продуктов взрыва в шпуре, Па; N – число шпуров в ряду, шт.; dbh – диаметр шпура, м; Lbh – глубина шпура, м;
где σdrupt – динамический предел прочности на растяжение, Па;
σdrupt = KweakKfKi[σdrupt], (4)
где Kweak – коэффициент структурного ослабления массива, Kweak = 0.2–0.4;
Ki – коэффициент динамичности (для гранитов 4–5.7)1; Kf – акустический показатель трещиноватости; Ср.rm, Ср – скорости продольной волны в массиве и образце горной породы, м/с.
Сила, которую необходимо приложить на преодоление трения блока по подошве при его перемещении:
F2 = Ffr = f1G cos α, (5)
где f1 = tg α – коэффициент трения; G – масса монолита, кг:
G = ρrmBHbenchW, (6)
где ρrm – плотность горной массы, кг/м3; W – линия наименьшего сопротивления, м; F3 – сила, позволяющая учитывать угол падения пласта, Па::
F3 = G sin α. (7)
Решение уравнений (1)–(7) позволяет получить выражение для расчета количества шпуров:
Протяженность отделяемого блока
где а – расстояние между шпуровыми зарядами, м:
Выбирая тип ВВ (для нашего случая ЗЭТ «Гранилен 1,2») и используя формулу Нобля–Абеля [25], определяем массу ВВ, которую необходимо взорвать в объеме шпура, чтобы создать требуемое давление продуктов детонации Рbp (11):
где Т0 – начальная температура, Т0 = 273 К; n – число молей газообразных продуктов взрыва; Тbl – температура продуктов взрыва, К; Р0 – атмосферное давление, Па,Р0 = 0,1 МПа.
При взрывном отделении монолита от массива трещины и сколы камня создаются в местах, в которых возникают импульсные реакции, интенсивность которых достаточна для скола породы и которая определяется конструкцией заряда, его мощностью, местоположением в отделяемом монолите [26–28].
При наличии пластовой трещины глубина размещенного заряда (эксцентриситет) определяется из выражения
где Н – высота монолита, м; W – ширина (мощность) монолита, м.
В случае отсутствия пластовой трещины глубина размещения заряда определяется из выражения
где fd и f′d – коэффициенты динамического трения в верхней и нижней вершинах монолита. Для приближенных расчетов можно принять fd = 0.25; f′d = 0.5.
Оптимальная ширина (мощность) монолита определяется из выражения
где hch – высота заряда, м; m – недобур, м.
На основании приведенной методики были рассчитаны параметры буровзрывных работ для отделения монолита с использованием зарядов ЗЭТ «Гранилен-2», которые представлены в табл. 1. Наряду с определением основных параметров БВР важнейшим условием для добычи качественных камнеблоков являются точность оконтуривания отделяемого монолита и обеспечение минимального радиуса наведенной трещиноватости в околошпуровой зоне.
Таблица 1
Расчетные параметры БВР для выкалывания камнеблоков при наличии подошвенной трещины (dbh = 42 мм, dch = 15 мм, lbh =2.9 м)
| Наименование | Расстояние между шпурами, м | |||
| 0.3 | 0.4 | 0.5 | 0.6 | |
| Масса заряда в шпуре, кг | 0.27 | 0.36 | 0.45 | 0.54 |
| Общий вес заряда, кг | 22.4 | 22.7 | 22.5 | 22.7 |
| Число шпуров | 83 | 63 | 50 | 42 |
| Давление в шпуре, МПа | 31.0 | 42.5 | 55.5 | 67.0 |
| Ожидаемый радиус наведенной трещиноватости, м | 0.026 | 0.03 | 0.035 | 0.038 |
| Длина заряда в шпуре, м | 0.75 | 0.84 | 1.4 | 1.7 |
Значения этих отклонений определяются коэффициентом сближения зарядов, равным
где а – расстояние между шпурами, м;
Следовательно, минимальные величины шероховатости граней монолита могут быть достигнуты при оптимальном значении n.
В результате проведенных экспериментов на гранитных карьерах блочного камня получена зависимость величины отклонения контура блоков в зависимости от расстояния между шпуровыми зарядами ЗЭТ «Гранилен-2» (рис. 1).

Рис. 1. Зависимость шероховатости поверхности блока от расстояния между шпурами
При низкоскоростном режиме нагружения и взаимодействии волн напряжений формируется асимметричное поле напряжений вокруг контурных шпуров, что приводит к детерминирующему росту магистральной трещины в плоскости отрыва.
Поскольку микротрещины возникают под действием импульса растягивающих напряжений, то их поверхности совпадают с радиальными плоскостями. Контурная трещина растягивается одновременно на нескольких структурных трещинах путем слияния микротрещин в макротрещины [29]. Как следствие, по линии, соединяющей соседние заряды, массив ослабляется под влиянием растягивающих напряжений по контурной линии, и между шпурами начинает расти магистральная трещина, а рост побочных трещин приостанавливается [30–31].
Результаты работ [25], [32] свидетельствуют, что радиус зоны наведенной трещиноватости в выкалываемом монолите зависит как от величины заряда в шпурах, так и от расстояния между ними. Кинетика разрушения при направленном расколе определяется как физико-механическими свойствами горных пород, так и параметрами напряжений и давления, создаваемых продуктами взрыва в зарядной полости.
При взрыве системы цилиндрических зарядов происходит взаимодействие волн напряжений, что приводит к трансформации поля напряжений.
Приближенный метод оценки полей напряжений на основе численного моделирования и использования аналитического расчета проводился по методике, изложенной в работах для взрыва зарядов с воздушным зазором.
В качестве взрывчатого вещества принимался ЗЭТ «Гралинен-1» диаметром dch = 11 мм с теплотой взрыва Q = 1550 кДж/кг. Заряды располагались в шпурах dbh = 42 мм в гранитном массиве с плотностью породы ρrocks = 2200 кг/м3, скорость продольной волны Сp = 6200 м/с.
Условие взаимодействия волн напряжений, обеспечивающих прорастание магистральной трещины, определялось из выражения
где σϕ1 и σϕ2 – соответственно амплитуды тангенциальной составляющей волны напряжений от взрыва соседних зарядов; a – между зарядами, м; σ*dynrupt – динамический предел прочности на отрыв для гранита, Па.
Тогда [33],
где σstrupt – статический предел прочности на отрыв, σstrupt = 9,1 МПа, σ*dynrupt = 36,4 МПа.
Эта величина принималась за предельный уровень напряжений, ниже которой не происходит прорастания магистральный трещины.
Длина естественной микротрещины l0 для гранитов по данным работ [33] составляла 0,01–0,03 см.
Максимальное амплитудное давление на стенки шпура для гранитов не должно превышать 90 МПа [25].
1Дамбаев Ж. Г. Физические основы направленного разрушения горных пород и технологии щадящего взрывания при отбойке блочного камня. Автореферат дис. … докт. техн. наук. Санкт-Петербург; 2000. 37 c.
Результаты
На рис. 2–4 представлены результаты расчета поля максимальных тангенциальных растягивающих напряжений при взрыве системы из двух зарядов ЗЭТ «Гранилен-1», расположенных на расстояниях 0,47 и 0,58 м. Заряды инициировали одновременно с помощью нити ДШЭ-12, пропущенной через канал заряда. Линейная плотность заряжания составляла 0,14 и 0,16 кг/м.
Из результатов следует, что взаимодействие одновременно взрываемых зарядов приводит к существенному изменению поля напряжений в окрестности плоскости, проходящей через заряды.
Очевидно, что если для одиночного заряда напряжение непрерывно убывает с расстоянием, то для взаимодействующих зарядов напряжение сначала убывает с удалением от зарядов, а затем вновь увеличивается, достигая на половине расстояния между зарядами максимума. На рис. 5 представлена расчетная зависимость индивидуальных тангенциальных растягивающих напряжений при линейной плотности заряжания q 0,14 and 0,16 кг/м и расстоянии между зарядами a 0,6 м.
Приведенные на рис. 5 данные позволяют оценить возможные зоны наведенной трещиноватости вокруг шпура.
Приведенные зависимости позволяют оценить возможные зоны наведенной трещиноватости вокруг шпура при различных плотностях заряжания.
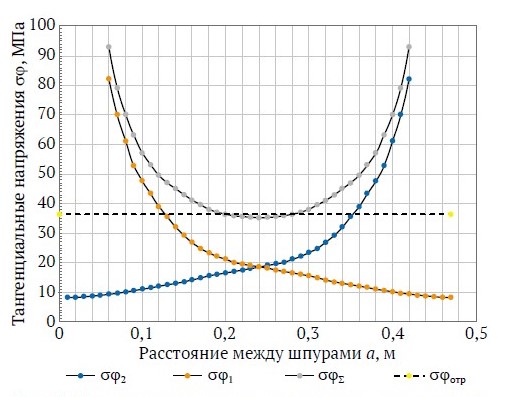
Рис. 2. Индивидуальные и суммарные тангенциальные напряжения при взрыве смежных зарядов (a = 0,47 м, q = 0,14 кг/м): σϕ1 и σϕ2 – амплитуды тангенциальной составляющей волны напряжения от первого и второго зарядов соответственно, МПа; σϕΣ – суммарная амплитуда тангенциальной составляющей волны напряжения от двух зарядов, МПа; σотр (σrupt) – предельно допустимое значение отрыва, МПа
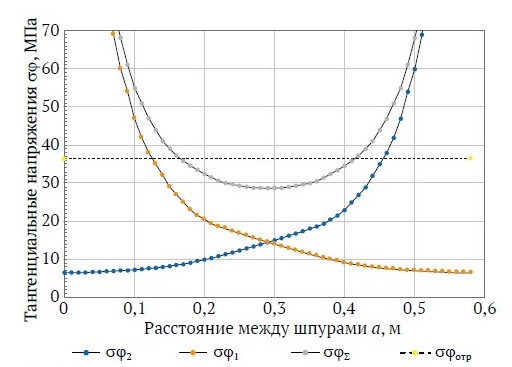
Рис. 3. Индивидуальные и суммарные тангенциальные напряжения при взрыве смежных зарядов (a = 0,58 м, q = 0,14 кг/м): σϕ1 и σϕ2 – амплитуды тангенциальной составляющей волны напряжения
от первого и второго зарядов соответственно, МПа; σϕΣ – суммарная амплитуда тангенциальной составляющей волны напряжения от двух зарядов, МПа; σотр (σrupt) – предельно допустимое значение отрыва, МПа

Рис. 4. Индивидуальные и суммарные тангенциальные напряжения при взрыве смежных зарядов (a = 0,58 м, q = 0,16 кг/м): σϕ1 и σϕ2 – амплитуды тангенциальной составляющей волны напряжения
от первого и второго зарядов соответственно, МПа; σϕΣ – суммарная амплитуда тангенциальной составляющей волны напряжения от двух зарядов, МПа; σотр (σrupt) – предельно допустимое значение отрыва, МПа

Рис. 5. Зона наведенной трещиноватости при линейных плотностях заряжания q1 = 0,14 кг/м, q2 = 0,16 кг/м: rтр – радиус трещиноватости, м; σотр (σrupt) – предельно допустимое значение отрыва, МПа
Заключение
Установлено, что для наиболее вероятного развития радиальной магистральной трещины между шпуровыми зарядами при добыче камнеблоков необходимо использовать эффект взаимодействия волн напряжений.
Следует отметить, что для минимизации зоны наведенной трещиноватости необходимо величину заряда выбирать таким образом, чтобы поле растягивающих напряжений в плоскости раскола не превышало предела прочности на отрыв. Прорастание на магистральной трещине начинается с момента прихода волны разрежения, отраженной от поверхности выкалываемого монолита.
Также можно утверждать, что с ростом среднего давления Рavr длина магистральной трещины убывает за счет роста числа микротрещин. Даже при максимальном значении давления на стенки шпура длина трещины от отдельного шпура такова, что с учетом возрастания коэффициента интенсивности напряжений и линейной системы трещин, прорастающих между шпурами, расстояние между ними может быть значительно больше обычно принятого.
Однако при малом значении давления (малом числе трещин) это потенциально возможное расстояние между шпурами нельзя реализовать из-за случайного направления роста трещин и, следовательно, непредсказуемости направления раскола. Поэтому необходимо увеличивать заряд (вместимость, давление в шпуре) для увеличения числа трещин с тем, чтобы в направлении линии шпуров или вблизи их обязательно имелись трещины.
При одновременном росте величины заряда приходится сближать шпуры, чтобы достаточно рано прекратился рост трещин, идущих от шпуров во всех направлениях (что происходит, как только трещины, растущие в направлении линии шпуров, начинают «чувствовать друг друга»), и нарушенная зона вокруг шпуров была бы минимальной.
Таким образом, получение направленного раскола требует сближения шпуров и одновременно увеличения в определенных пределах шпурового заряда.
Потенциальную возможность направленного раскола при увеличенном расстоянии между шпурами со снaиженными зарядами можно реализовать, используя возможные выделенные естественные направления в камне (кливаж, слоистость и т.п.), что исключает рост трещин в других направлениях.
Список литературы
1. Careddu N. Dimension stones in the circular economy world. Resources Policy. 2019;60:243–245. https://doi.org/10.1016/j.resourpol.2019.01.012
2. Paramonov G. P., Kovalevskyi V. N., Mysin A. V. Determination of the conditions of an effective functioning of elongated cumulative charges in processing the marble stone. Key Engineering Materials. 2020;836:19–24. https://doi.org/10.4028/www.scientific.net/kem.836.19
3. Боровиков В. А., Ванягин И. Ф. К расчету параметров волн напряжений при взрыве удлиненного заряда в горных породах. Взрывное дело. 1976;(76/38):74–85.
4. Ишейский В. А., Рядинский Д. Э., Магомедов Г. С. Повышение качества дробления горных пород взрывом за счет учета структурных особенностей взрываемого массива. Горный информационно-аналитический бюллетень. 2023;(9–1):79–95. https://doi.org/10.25018/0236_1493_2023_91_0_79
5. Ковалев А. В. Направления совершенствования взрывной технологии добычи блочного камня в массиве с интенсивной трещиноватостью. Горные науки и технологии. 2018;(1):23–34. https://doi.org/10.17073/2500-0632-2018-1-23-34
6. Pal Roy P. Emerging trends in drilling and blasting technology: concerns and commitments. Arabian Journal of Geosciences. 2021;14:652. https://doi.org/10.1007/s12517-021-06949-z
7. Sanchidrián J. A., García-Bermudez P., Jimeno C. L. Optimization of granite splitting by blasting using notched holes. International Journal for Blasting and Fragmentation. 2000;4(1):1–11. https://doi.org/10.1080/13855140009408059
8. Господариков А. П., Ревин И. Е., Морозов К. В. Композитная модель анализа данных сейсмического мониторинга при ведении горных работ на примере Кукисвумчоррского месторождения АО «Апатит». Записки Горного института. 2023;262:571–580. https://doi.org/10.31897/PMI.2023.9
9. Барон Л. И., Турчанинов H. A., Ключников A. B. Нарушенность пород при контурном взрывании. Л.: Наука; 1975. 339 с.
10. Боровиков В. А., Ванягин И. Ф. Техника и технология взрывных работ. Л.: Изд-во ЛГИ; 1985. 92 с.
11. Зырянов И. В., Бондаренко И. Ф., Ковалевич С. В., Ким С. И. Влияние взрыва скважинного заряда с радиальным зазором на качество разрушения алмазоносной руды. Горный информационно-аналитический бюллетень. 2022;(5–2):58–71. https://doi.org/10.25018/0236_1493_2022_52_0_58
12. Маринин М. А., Евграфов М. В., Должиков В. В. Производство взрывных работ на заданный гранулометрический состав руды в рамках концепции «mine-to-mill»: современное состояние и перспективы. Известия Томского политехнического университета. Инжиниринг георесурсов. 2021;332(7):65–74. https://doi.org/10.18799/24131830/2021/7/3264
13. Saadati M., Forquin P., Weddfelt K. et al. On the mechanical behavior of granite material with particular emphasis on the influence from pre-existing cracks and defects. Journal of Testing and Evaluation. 2018;46:33–45. https://doi.org/10.1520/JTE20160072
14. Zhang Z. X., Chi L. Y., Qiao Y. Fracture initiation, gas ejection, and strain waves measured on specimen surfaces in model rock blasting. Rock Mechanics and Rock Engineering. 2021;54:647–663. https://doi.org/10.1007/s00603-020-02300-2
15. Borowski G., Smirnov Yu., Ivanov A., Danilov A. Effectiveness of carboxymethyl cellulose solutions for dust suppression in the mining industry. International Journal of Coal Preparation and Utilization. 2020;42(8):2345–2356. https://doi.org/10.1080/19392699.2020.1841177
16. Cardu M., Saltarin S., Todaro C., Deangeli C. Precision rock excavation: beyond controlled blasting and line drilling. Mining. 2021;1(2):192–210. https://doi.org/10.3390/mining1020013
17. Лещинский А. В., Шевкун Е. Б., Лысак Ю. А. Управление дроблением железных руд взрывом – путь повышения эффективности обогатительного передела. Горный информационно-аналитический бюллетень. 2019;(4):41–52. https://doi.org/10.25018/0236-1493-2019-04-0-41-52
18. Дарбинян Т. П., Цымбалов А. А., Зубов В. П., Колганов А. В. Влияние трещиноватости горного массива на разубоживание медно-никелевых вкрапленных руд при добыче их на руднике «Октябрьский». Горный журнал. 2023;(6):19–26. https://doi.org/10.17580/gzh.2023.06.03
19. Молдован Д. В., Чернобай В. И., Ястребова К. Н. Влияние композитного материала в конструкции забойки на ее работоспособность. Горный информационно-аналитический бюллетень. 2023;(9–1):110–121. https://doi.org/10.25018/0236_1493_2023_91_0_110
20. Протосеня А. Г., Беляков Н. А., Буслова М. А. Моделирование напряженно-деформированного состояния блочного горного массива рудных месторождений при отработке системами разработки с обрушением. Записки Горного института. 2023;262:619–627. URL: https://pmi.spmi.ru/pmi/article/view/15942
21. Раджаоалисон Х., Злотковски А., Рамболаманана Г. Определение механических свойств песчаника неразрушающим методом. Записки Горного института. 2020;241:113–117. https://doi.org/10.31897/pmi.2020.1.113
22. Панасюк В. В. Предельное равновесие хрупких тел с трещинами. Киев: Наукова думка; 1991. 411 с.
23. Бычков Г. В., Кокунина Л. В., Казаков С. В. Буровзрывной способ добычи монолитов и блоков природного камня. Горный журнал. 2008;(1):45–49.
24. Blair D. P. Dynamic response of mine pit walls. International Journal of Rock Mechanics and Mining Sciences. 2018;106:14–19. https://doi.org/10.1016/j.ijrmms.2018.04.002
25. Зубов В. П., Ли Юньпэн. Слоевая система разработки мощных пологих угольных пластов на шахтах Китая: проблемные вопросы, направления совершенствования. Горный информационно-аналитический бюллетень. 2023;(7):37–51. https://doi.org/10.25018/0236_1493_2023_7_0_37
26. Конгар-Сюрюн Ч. Б., Ковальский Е. Р. Твердеющие закладочные смеси на калийных рудниках: перспективные материалы, регулирующие напряжённо-деформированное состояние массива. Геология и геофизика Юга России. 2023;13(4):177-187. https://doi.org/10.46698/VNC.2023.34.99.014
27. Ефремов Э. И., Кравцов B. C., Мячина H. H. и др. Основы теории и методы взрывного дробления горных пород. Киев: Наукова думка; 1979. 224 с.
28. Аленичев И. А., Рахманов Р. А. Исследование эмпирических закономерностей сброса горной массы взрывом на свободную поверхность уступа карьера. Записки Горного института. 2021;249:334–341. https://doi.org/10.31897/PMI.2021.3.2
29. Elkarmoty M., Colla C., Gabrielli E. et al. A combination of GPR survey and laboratory rock tests for evaluating an ornamental stone deposit in a quarry bench. Procedia Engineering. 2017;191:999–1007. https://doi.org/10.1016/j.proeng.2017.05.272
30. Нефедов М. А. Направленное разрушение горных пород взрывом. СПб.: Изд-во С.-Петербургского университета; 1991. 188 с.
31. Мешков А. А., Афанасьев П. И. Физические основы взрывного разрушения горных пород. Монография. М.: Горная книга; 2021. 124 с.
32. Чертков В. Я. Теоретическая оценка повышенной микротрещиноватости при взрывной отбойке блочного камня. Физико-технические проблемы разработки полезных ископаемых. 1983;(1):36–43.
Об авторах
В. Н. КовалевскийРоссия
Владимир Николаевич Ковалевский – кандидат технических наук, доцент кафедры взрывного дела
Scopus ID 57194598687, ResearcherID AAD-5379-2019
г. Санкт-Петербург
А. В. Мысин
Россия
Алексей Владимирович Мысин – кандидат технических наук, ст. преподаватель кафедры геоэкологии
Scopus ID 57196262504
г. Санкт-Петербург
В. И. Сушкова
Россия
Вероника Ивановна Сушкова – аспирант кафедры взрывного дела
Scopus ID 58121433200
г. Санкт-Петербург
Рецензия
Для цитирования:
Ковалевский В.Н., Мысин А.В., Сушкова В.И. Теоретические аспекты технологии взрывной отбойки блочного камня. Горные науки и технологии. 2024;9(2):97-104. https://doi.org/10.17073/2500-0632-2023-12-187
For citation:
Kovalevsky V.N., Mysin A.V., Sushkova V.I. Theoretical aspects of block stone blasting method. Mining Science and Technology (Russia). 2024;9(2):97-104. https://doi.org/10.17073/2500-0632-2023-12-187



































