Statistical analysis of determining porosity factor of oil and gas reservoir rocks using gas volumetry and X-Ray tomography methods

Introduction

One of the most important characteristics that allow for the estimation of reserves and are taken into account in the prospecting, exploration, and development of oil and gas fields is porosity factor K_p. Despite the existence of the problem of scaling physical characteristics between a reservoir and individual samples [1, 2], the most accessible and reliable methods of studying are direct laboratory petrophysical testing of core samples, among which the estimation of a porosity factor is one of the most accurate and reliable.

Over the past two decades, a significant number of publications with the results of tomographic studies of a core have appeared. The works of foreign and domestic researchers provide data for samples of various sizes and lithology. Thus, the works [3, 4] are devoted to reviewing the capabilities of the method in a number of types of geological research, including the study of carbonate reservoir rocks. The papers [5, 6] are devoted to the study of marine sediment cores. Although statistical analysis of the porosity of terrigenous and carbonate sediments is carried out in [6], unfortunately, it only applies to full-size samples, which were the subject of the study. The papers [7, 8] are also review papers, providing only general descriptions of the principles of tomography and examples of the method's use without statistical analysis. The paper [9] presents experience on core porosity research, but due to low resolution, the authors limit themselves to calculating cavernous porosity. The authors of [10] compared the results of porosity measurements obtained by tomography and gas volumetry with breakage by lithology, but only 14 samples were studied. In addition, for tomography, the samples were cut into cylinders with sides of 5–20 mm that significantly affected the results. Thus, a full statistical comparison of determining the porosity of samples of standard sizes by X-ray tomography and other methods, taking into account the peculiarities of the lithology of the studied reservoirs, has not been carried out, although some researchers recognize the need for such a comparison [11].

To address the current challenges in oil industry related to modeling the pore space structure in a 3D core model and evaluating permeability and porosity ("Digital Core"), it is necessary to obtain a representative characteristic of a void space. A similar characteristic is required to solve geotechnical problems related to modeling and evaluating the strength properties of heterogeneous rocks. In addition, it is important for research on capillary processes in porous media.

Laboratory petrophysical studies of core samples allow to evaluate only a single integral characteristic of a core sample, comprising the effective porosity and total porosity of a sample. However, for computer 3D modeling of various processes in a rock core, such integral values are insufficient that necessitates the use of non-destructive volumetry methods for researching core samples, such as X-ray computer tomography (CT), which allows for the study of the internal heterogeneity of core samples in volume. The application of CT, despite its modernity and technological nature, has a number of problems associated with the method's resolution for evaluating the heterogeneity of rock in the region of physical small-scale heterogeneities (small pores), that is, microporosity.

In order to bring the porosity estimates determined by different methods to a unified value, the study included a statistical analysis of the values of porosity factors obtained from standard laboratory petrophysical studies of core samples and from the results of a core CT.

The aim of this work is to develop statistical models for assessing the discrepancy between the porosity factor K_p determined using computer tomography (CT) data and more reliable laboratory petrophysical data for terrigenous and carbonate rocks. The assessment of this discrepancy will enable the estimation of the proportion of microporosity in computer 3D core models based on the CT results. The separate consideration of terrigenous and carbonate rocks is due to the significant differences in mineralogical composition, structural-textural features of the sediments, and pore space structures of these two main lithological types of sedimentary rocks.

The research objectives include:

• An assessment of the impact of lithology on the K_p assessment using various methods (petrophysics and CT)
• An assessment of the influence of the K_p variation range on the convergence of the results of these two methods (petrophysics and CT) for different lithologies
• Building models for adjusting K_p values based on CT results for different lithologies.

The solution to these problems is based on a detailed statistical analysis.

Theory

There are two standard methods for determining porosity factor that are widely used in petrophysics, which differ in a phase used: determination of porosity by liquid saturation and determination of porosity by gas (gas volumetry). These methods do not measure the entire pore volume, but only those pores that are connected to a sample surface and to each other, which, according to classification [12], constitute effective porosity. The use of liquid or gas allows them to be filled and the entire volume of these open and connected pores to be measured with sufficient accuracy. Of course, there is also a method for measuring total and closed porosity (K_p estimation through mineralogical density), but it is less commonly used because it requires the destruction of samples [13].

At the same time, in recent years, a relatively new method of studying pore space has become increasingly widespread in petrophysical research, computer X-ray tomography. This method allows the visualization of the pore space inside a sample, which makes it possible to qualitatively assess the porosity and establish a relationship between its distribution and the lithological characteristics of the sample being studied. However, the main disadvantage of using the X-ray computer tomography method in a standard petrophysical research complex is its low resolution. This method can only visualize pores that are up to a few micrometers in size that leads to a significant underestimation of the volume of the pore space, resulting in a porosity factor calculated using the X-ray tomography method being lower than that measured by standard liquid saturation and gas volumetry methods.

It can be assumed that the degree of closeness of the porosity factor values calculated using the gas volumetry-liquid saturation methods and the X-ray tomography method will depend significantly on the dominant sizes and quantitative ratios of individual pore types in a studied core sample: open (effective porosity) and closed, connected and isolated, large and small. In the opinion of the authors of this paper, this will mainly be determined by the samples lithology. Among the types of reservoir rocks studied, the pore space structure will differ most significantly between carbonate and terrigenous rocks.

Carbonate reservoirs are known to have an extremely heterogeneous pore space structure, consisting of intergranular and intragranular pores, cavities, and fractures. Often in some types of carbonate reservoirs, for example, in  grainstone structural type of limestones [14], most of the reservoir space can be represented by large cavities and fractures, which makes it easily visualizable using X-ray tomography. At the same time, the nature of the structure of the carbonate pore space does not exclude the presence of a certain proportion of closed pores in a sample, which may not be detected by gas volumetry and liquid saturation methods, which are only capable of measuring effective (open) porosity. Therefore, it can be expected that the porosity factors of carbonate rocks determined by standard methods and by X-ray tomography may be close in value to each other, but at the same time be composed of different volumes.

The pore space of terrigenous reservoir rocks is characterized by greater homogeneity and connectivity due to its predominantly intergranular nature. Rocks of this composition form granular-type reservoirs, closely described by the Slichter model, in which permeability is determined by porosity and particle diameter [15]. At the same time, the dimensions of individual elements of the void space in this type of rock are smaller than the resolution limit of the X-ray tomography method. It should be noted that, despite the existence of high-resolution micro- and nanotomography methods, these methods can only be used for separately manufactured samples of millimeter dimensions, as shown in [16] that excludes comparison with the determination of the porosity factor using standard methods carried out on cylindrical samples with a standard diameter of 30 or 25 mm.

Thus, this study compares the porosity factors obtained by different methods on the same standard-size samples of carbonate and terrigenous rocks.

Research Materials and Techniques

The studied samples of core from the oil fields of the Perm region were cut from full-size cores into cylinders with a standard diameter and a height of 30 mm. The samples belonged to two lithologies: terrigenous and carbonate rocks.

The terrigenous samples were mainly represented by sandstone, silt-rich sandstone composed of quartz and feldspar-quartz; gray, dark gray, brown, and brown; fine-grained, medium-fine-grained, and coarse-grained; of varying degrees of sorting; orthomorphic or cemented with clayey, calcite, or ferruginous cement; strong or of medium strength, with mineral inclusions of mica, ore minerals, and pyrite.

The carbonate samples were represented by limestone, dolomite, and dolomitized limestone light gray, gray, dark gray; organogenic, detrital, organogenic-detrital, lumpy-detrital, lumpy-algal, and algal; sometimes slightly clayey and clayey; porous, porous-cavernous, and cavernous; strong with frequent stylolitic joints and cracks sometimes filled with calcite crystals.

The research involved measuring porosity using the gas volumetry method (K_p, %) and X-ray computer tomography (K_p^t, %).

The gas volumetry method was chosen by the authors for several reasons: firstly, this method is quite fast (on average, it takes no more than an hour to measure one sample) and relatively simple, and, as a result, it is most often used in petrophysical laboratories; secondly, the use of a chemically inert gas instead of a liquid allows to reliably exclude changes in the samples caused, for example, by accidental violation of the procedure of washing and drying a sample after the saturation test or chemical interaction between the liquid and the mineral matrix of a sample.

Porosity measurements were performed on an AP-608 automated porosimeter-permeameter (Coretest Systems, USA). The principle of operation of this unit is based on the method of non-stationary filtration [17].

The essence of the method lies in measuring a pore volume using the principle of helium expansion according to Boyle's law, which states that the pressure P of any ideal gas multiplied by its volume V gives a constant value at a constant temperature. In the context of core analysis, Boyle's law allows to determine an unknown volume by the expansion of a gas with known pressure and temperature values into an empty space and using the resulting pressure to calculate the unknown volume. Therefore, knowing P₁, P₂ and V₂, it is possible to calculate V₁:

V₁ = (P₂·V₂)/P₁. (1)

In a AR-608 porosimeter-permeameter, helium is pumped in from both ends of a sample. The permeability range of samples available for measurement on this unit is from 0.001 mD (rocks with such permeability are not considered to be reservoirs) to 5000 mD. Accordingly, the porosity measuring range is from 0.1 to 40%, which also covers the ranges typical of terrigenous and carbonate reservoirs.

The method of sample preparation and measurement complies with GOST¹ and involved pre-drying of samples that were carefully extracted in an alcohol-benzene mixture using a drying cabinet. The drying time and temperature were at least 8 h and 105°C for the carbonate rocks and at least 12 h and 80°C for the terrigenous rocks. After drying, the samples were cooled in a desiccator, their geometric characteristics were measured using an electronic caliper, and then the porosity factor was determined using the AR-608 unit. All measurements were taken at least five times, and the arithmetic mean was calculated based on the results of all five measurements, which was the final value for each sample.

The second method analyzed in the paper is X-ray computer tomography of a core. The method was developed by A. Cormack and G. Hounsfield [18] and is based on Radon transformations [19]. The essence of the method lies in creating a series of X-ray images obtained when X-rays pass through a sample rotating along a single axis. The resulting X-ray images are transformed through the inverse transform of the integral of a function of a straight line perpendicular to a vector that is directed along the direction of the radiation at a certain distance measured along it.

In our study, an X-ray inspection system with a computer tomography function, Nikon XT H 225 (Nikon Metrology, Great Britain) was used for X-ray tomography. This system consists of a stationary X-ray source forming a focal spot measuring 3 µm, a three-position rotating table, and a 2048×1408 pixel detector with a physical pixel size of 142 µm. The system allows studying samples of a standard diameter of 30 mm with a resolution of up to 20 μm.

Samples were surveyed at a radiation source voltages ranging from 150 to 180 kV, current strengths ranging from 100 to 150 mA, using a 0.5 mm thick copper filter, exposure time of 0.5 s, and at least 3000 images. All samples were positioned so that the resolution of the resulting reconstruction was at least 25 μm. Inhomogeneities smaller than 1 voxel (25 µm) are referred to as microporosity, which, unlike larger macroporosity, cannot be distinguished with high accuracy and directly geometrically identified in a sample. In practice, a number of assumptions are made to identify such porosity in samples. For example, that the micropores are located on the surface of large pores, or micropores can be located in the contact areas of mineral grains, or they are distributed fairly evenly throughout the volume of a mineral matrix. However, for all these assumptions, it is necessary to estimate the proportion of this microporosity.

The reconstruction of a 3D image was performed using proprietary CT Pro 3D software (Nikon Metrology, UK), which uses an improved version of one of the most widely used FDK algorithms [20] for the reconstruction procedure. The reconstructed images were processed in the Avizo Fire program (Visualization Science Group, France).

The technique for processing the images of the samples in order to obtain the volume of the pore space was used as follows. In the initial reconstruction, a 32-bit black and white three-dimensional image, where the brightest areas correspond to areas of maximum density (mineral matrix), and the darkest areas correspond to the void space, a binarization procedure was performed. The essence of the binarization procedure is that the entire range of gray shades is divided into two volumes with values of 0 and 1, corresponding to the volumes of pores and matrix (Fig. 1).

Fig. 1. Distinguishing on a fragment of a black and white image of a rock:
A – reconstructed image of a sample cross-section in shades of gray, proportional to the absorption of the material (black – does not absorb, white – absorbs);
B – distinguishing void space in a black-and-white image of rock
(black – air in pores and around the sample; white – mineral matrix)

These volumes, in turn, can already be measured using software tools.

The porosity factor of the sample was calculated based on tomography data using the standard porosity calculation formula:

K_p^t =  V_por/V_vol · 100, (2)

where V_por is the volume of the binarized model of a sample pore space, mm³; V_vol is the volume of the binarized model of the entire sample space, mm³.

¹ GOST 26450.0-85–GOST 26450.2-85. Rocks. Methods for determining reservoir properties. М.: Standards Publishing House; 1985. 16 p. (In Russ.)

Findings and Analysis of the Data Obtained

This chapter deals with the statistical analysis of the porosity factor values obtained by the methods described above. Fig. 2 shows a comparison of the porosity factor values obtained by the gas volumetry method (K_p, %) and those obtained by the X-ray tomography method (K_p^t, %) for terrigenous and carbonate rocks.

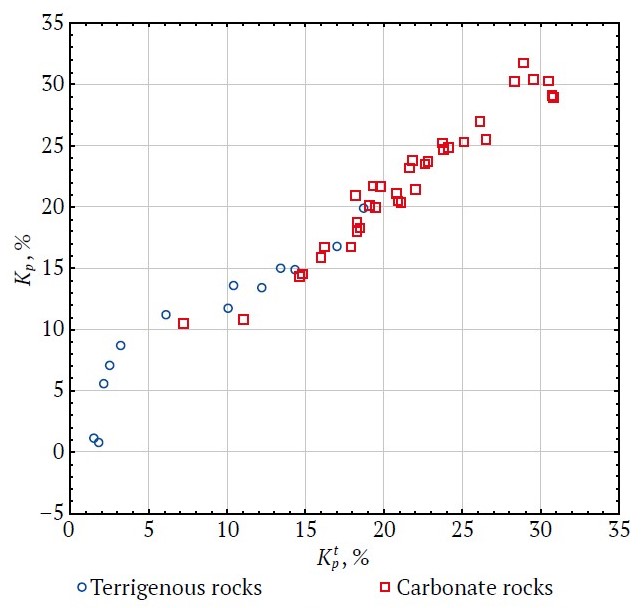
Fig. 2. Fields of correlation between K_p and K_p^t for different rocks

For terrigenous rocks, the average porosity values for K_p^t and K_p are 8.71 and 10.76%, respectively, with standard deviations of 6.17 and 5.82%.

For carbonate rocks, the average porosity values for K_p^t and K_p are 21.43 and 22.00%, respectively, with standard deviations of 5.51 and 5.43%.

The analysis of the given correlation fields shows that the relationships of the values of K_p and K_p^t for the studied rocks depend of the values range. For terrigenous rocks the values of K_p and K_p^t lower than those for carbonate ones. Comparisons of the average values of K_p and K_p^t for the studied rocks were performed using Student's t-test and are presented in Table 1.

Table 1

Comparison of average values of K_p and K_p^t for different rock types

It can be seen from here that the average values of the porosity factors, determined by different methods, do not statistically differ (the level of significance achieved p > 0.05). At the same time, visual analysis of the fields of correlation between K_p and K_p^t for both terrigenous and carbonate rocks shows that within the correlation fields, different relationships are observed depending on the values of K_p and K_p^t. Overall, the results of the evaluation of the average K_p and K_p^t are not statistically contradictory to each other, but require a more detailed examination by the porosity ranges. At the same time, the average values obtained by CT method are always lower, despite the different lithology that indicates the complexity and some underestimation of K_p for microporosity due to the physical limitations of the CT method.

To determine various relationships between K_p and K_p^t, we subdivided them by lithology and K_p range and arrange the values of K_p of the samples in ascending order, where their number increased by one (n = 3, n = 4, n = 5, …, n = 33 for carbonate rocks and n = 13 for terrigenous rocks). The total number of models considered was determined by the sample collection amount. For each considered range of values of K_p, we performed a K_p = f(K_p^t) regression analysis by n values with assessing the paired correlation coefficient r and statistical characteristics of the regression equation coefficients.

The regression equation is as follows:

K_p = b + k∙K_p^t, (3)

where K_p is porosity factor obtained by the gas volumetry method, %; K_p^t is porosity factor obtained by X-ray tomography, %; b is intercept (free term) in the regression equation; k is slope in the regression equation.

For carbonate rocks, the regression equation parameters are given in Table 2.

Table 2

Regression equations for K_p dependence on K_p^t (carbonate rocks)

* – statistically significant values (p ≤ 0.05).

33 regression equations were built for carbonate rocks, and the correlation coefficient values r ranged from 0.892 to 0.975.

The statistical characteristics of the developed models were used to build dependencies of the values of the intercepts of the regression equations and the slopes for K_p^t on the values of the correlation coefficients r (Figs. 3–5).

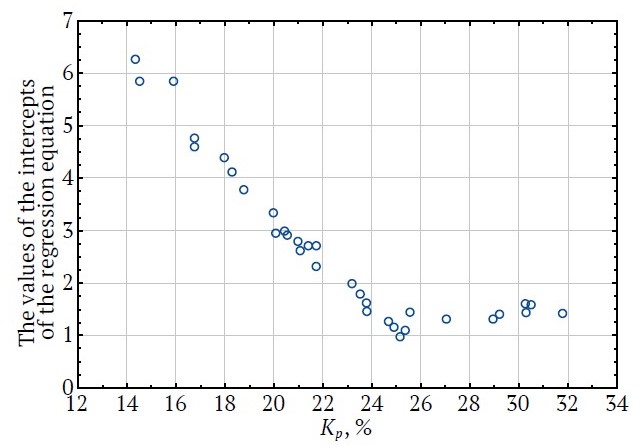
Fig. 3. The values of intercepts of the regression equations depending on K_p (carbonate rocks)

The analysis shows that the relationships between the studied parameters are of two types: at K_p < 24%; when increasing the range of K_p, there is a regular decrease in an intercept value; with even greater increase of K_p, the value of an intercept changes insignificantly.

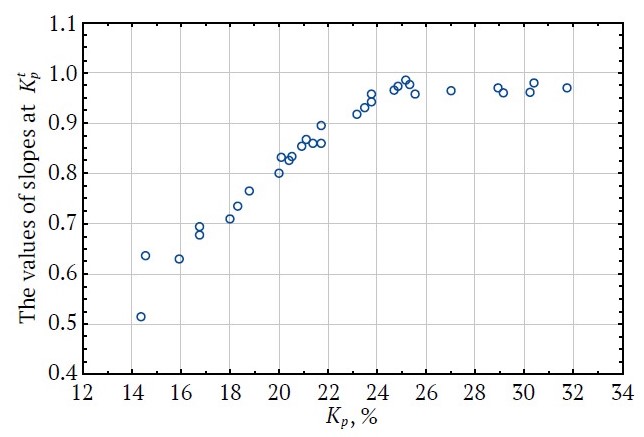
Fig. 4.  Slope at K_p^t in regression equations depending on K_p (carbonate rocks)

The analysis shows that the relationships between the studied parameters are also of two types: at K_p < 24%, when increasing  K_p, there is a regular increase in the slopes at K_p^t; with even greater increase of K_p, the values of the slopes changes insignificantly, being in a range of 0.97–0.98.

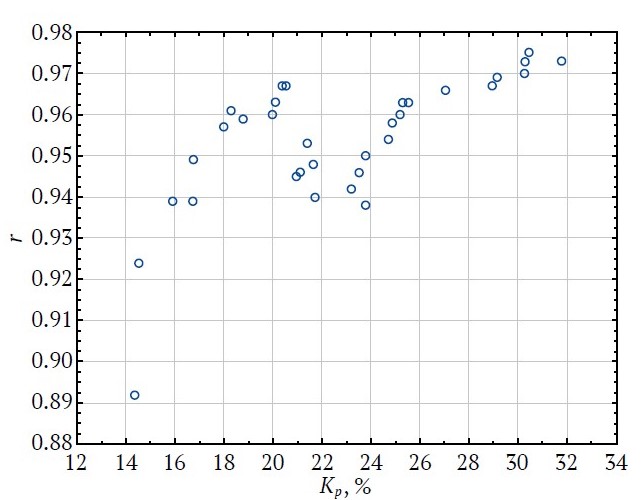
Fig. 5. Correlation coefficient r as a function of K_p (carbonate rocks)

It can be seen from here that the relationships between the studied parameters are also of two types: at K_p < 22%, when increasing K_p, there is an initial increase in r. At K_p < 23%, r decreases. With an even greater increase in the range of K_p, the values of the coefficients increase along a complex trajectory.

The above K_p and K_p^t dependency analysis for carbonate rocks showed that it seems possible to determine two boundaries that differentiate the values of K_p^t into three groups: the first one, when K_p^t < 16.0%; the second, at 16.0% ≤ K_p^t < 22.6%; and the third one, when K_p^t ≥ 22.6%.

The first group is at K_p^t < 16.0%, in which the dependency of K_p on K_p^t is statistically insignificant. At K_p^t from 16.0 to 22.6%, statistically significant correlations between the studied parameters were observed. To determine the values of K_p from K_p^t it is necessary to make an adjustment using the regression equation given in Table 4. At K_p^t ≥ 22.6%, it is also necessary to make an adjustment using the regression equation given in Table 3.

Table 3

Regression equations for K_p dependence on K_p^p (carbonate rocks)

Thus, the studies conducted showed that the values of K_p^t obtained by X-ray tomography for carbonate rocks, despite the statistical equality of the mean values, are characterized by different statistical relationships. At K_p^t < 16.0%, there is no significant correlation with K_p. This indicates that different values of porosity factors are obtained using these methods. At K_p^t ≥ 16.0%, the values of K_p^t and K_p are statistically interconnected. It should be noted that at certain intervals of the values, the intercepts values are statistically significant. This indicates that there is an adjustment of the values K_p by the intercepts of the regression equations. Therefore, to correctly use the values of K_p^t and K_p in carbonate rocks, it is necessary to use the obtained regression equations for the identified ranges of K_p.

A similar analysis was performed for terrigenous rocks (Table 4).

Table 4

Regression equations of K_p dependencies on K_p^t (terrigenous rocks)

* – statistically significant values (p ≤ 0.05).

11 regression equations were built for terrigenous rocks, and r values ranged from 0.806 to 0.937. The analysis of the intercepts of the regression equations showed that when K_p^t < 11.75%, the intercepts changed from negative to positive values. The values of slope at K_p^t  are also characterized by a regular change from higher values (more than 1) to lower values (less than 1). Correlation coefficients r trends are shown in Fig. 6.

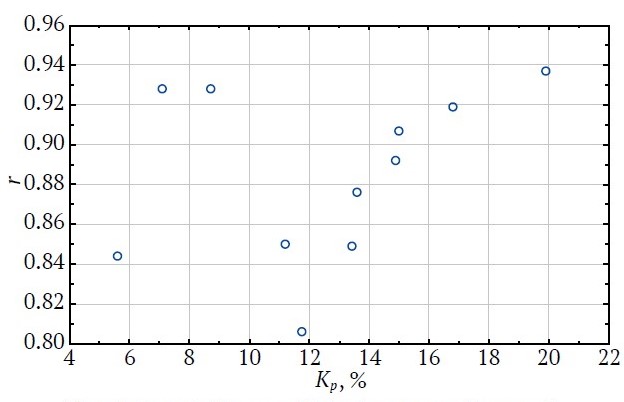
Fig. 6. Correlation coefficients r depending on K_p (terrigenous rocks)

The analysis shows that the relationships between the studied parameters are also of two types: when K_p < 12%, increasing K_p causes a chaotic change in the values of r; when the K_p range increases, there is a regular increase in r values from 0.849 to 0.937.

An analysis of the constructed regression equations showed that when K_p^t ≤ 7.1%, the dependence K_p on K_p^t is statistically insignificant. At K_p^t > 7.1% a statistically significant regression equation was obtained:

K_p = 6.349+0.63905 K_p^t, at r = 0.964, p = 0.00002. (4)

This indicates that the relationships between K_p and K_p^t are characterized by the presence of a statistical relation.

Practical Application and Areas of Further Research

Thus, the conducted research showed that these methods do not replace, but complement each other, as they have different limitations in application. At the same time, the statistical analysis carried out showed that the use of both methods gives naturally different, but statistically related results, which demonstrates the possibility of their joint application. It is also important that, when researching samples of different lithological types of collectors, the methods have different limitations:

1) In the study of carbonate samples, both methods showed statistically significant correlation coefficients between K_p и K_p^t at the values of K_p obtained by the gas volumetry method of above 16% that may be due to larger void sizes.

2) When testing terrigenous samples, porosity was most accurately determined at porosity factor values K_p more than 7.1% that may be due to poor filling of intergranular voids with cement or good sorting of the material.

The application of the recommended equations for the lithologies in different ranges of K_p enables an integral estimation of microporosity as the difference between the estimation of K_p according to the equation and the values of K_p^t obtained based on CT data. This is especially true for samples of irregular or complex shapes, which are not always possible to fully examine in a petrophysical laboratory. This integrated assessment of microporosity allows for a constraint on the total volume of distributable micropores, which will improve the quality of three-dimensional computer models of core and pore space of reservoir rocks.

The results of the study can be used for petrophysical substantiation of the permeability and porosity of reservoir rocks in oil and gas fields.

The use of the proposed approach enables improving the quality of 3D models of rock core, which will ultimately lead to an increase in the accuracy of various modeling methods related to rock properties, and will allow for more rational and economically efficient development of oil and gas fields (or other natural resources).

Further research areas appear to the authors in the continuation of the tests with an increase in the number and variety of samples that will enable a refinement of the obtained dependencies, as well as in the consideration of additional standard characteristics of core (values of a residual oil saturation factor, capillary curves, etc.).

Conclusion

The research carried out convincingly showed that when using the data on porosity factors obtained by different methods for both carbonate and terrigenous rocks, the results obtained should be comparable.

The results of the assessment of the averages of K_p and K_p^t for terrigenous and carbonate rocks are not statistically contradictory to each other. At the same time, the average values obtained by the CT method are always lower, despite the different lithology that indicates the complexity and some underestimation of K_p for microporosity due to the physical limitations and other features of the CT method.

The studies carried out showed that the values of K_p^t obtained by X-ray tomography for carbonate rocks, when K_p^t < 16.0%, have no statistical relationship with K_p. For the values outside this range, the equations for estimating and adjusting the K_p values were proposed.

An analysis of the constructed regression equations for terrigenous rocks showed that when K_p^t ≤ 7.1%, the dependence of K_p on K_p^t was statistically insignificant. For the values outside this range, the equations for estimating and adjusting the K_p values were proposed.

The application of the recommended equations for the lithologies by the range of K_p allows for an integral estimation of microporosity as the difference between the estimate of K_p according to the equation and the values of K_p^t obtained based on CT data. The proposed approaches make it possible to improve the quality of 3D models of the pore space structure of rocks.