Статистический анализ определения коэффициентов пористости пород-коллекторов нефти и газа методами газоволюметрии и рентгеновской томографии

Введение

Одной из важнейших характеристик, позволяющих проводить подсчет запасов и учитываемых при поисках, разведке и разработке месторождений нефти и газа, является коэффициент пористости K_п. Несмотря на существование проблемы масштабирования физических характеристик между коллектором и отдельными образцами [1, 2], наиболее доступными и надежными методами изучения являются непосредственные лабораторные петрофизические исследования образцов керна, среди которых оценка коэффициента пористости является одной из самых точных и достоверных.

За последние два десятилетия появилось значительное количество публикаций с результатами томографических исследований керна. В работах зарубежных и отечественных исследователей приведены данные для образцов различного размера и литологического состава. Так, работы [3, 4] посвящены обзору возможностей метода в обширных видах геологических исследований, в том числе и в изучении карбонатных пород-коллекторов. Статьи [5, 6] посвящены исследованиям кернов морских осадков, при этом хотя в работе [6] статистический анализ пористости терригенных и карбонатных отложений и проводится, однако, к сожалению, он относится только к полноразмерным образцам, которым и посвящена работа. Статьи [7, 8] также являются обзорными, в них даны лишь общие описания принципов томографии и приведены примеры использования метода без их статистического анализа. В статье [9] приводится опыт исследования пористости керна, однако вследствие невысокой разрешающей способности авторы ограничиваются расчетом каверновой пористости. Авторы работы [10] провели сопоставление результатов измерения пористости по томографии и газоволюметрии, сравнение по литотипам, однако исследовано было лишь 14 образцов, кроме того, для томографии образцы обрезались до цилиндров со стороной 5–20 мм, что значительно повлияло на результаты. Таким образом, полноценного статистического сравнения определения пористости образцов стандартных размеров методами рентгеновской томографии и другими методами с учетом особенностей литологии изучаемых коллекторов проведено не было, хотя некоторые исследователи признают необходимость такого сопоставления [11].

Для решения актуальных задач в нефтяной отрасли, связанных с моделированием структуры порового пространства в 3D-модели керна и оценкой фильтрационно-емкостных свойств («Цифровой керн»), необходимо получение представительной характеристики пустотного пространства. Аналогичная характеристика требуется для решения задач геомеханики, связанных с моделированием и оценкой прочностных свойств неоднородных горных пород. Кроме того, она важна для исследований капиллярных процессов в пористых средах.

Лабораторные петрофизические исследования образцов керна позволяют оценивать только единственную интегральную характеристику образца керна – коэффициенты открытой и общей пористости образца. Однако для компьютерного 3D-моделирования различных процессов в керне горных пород таких интегральных значений недостаточно, что вызывает необходимость применения неразрушающих объемных методов исследования образцов керна, таких как рентгеновская компьютерная томография (КТ), которая позволяет изучать внутреннюю неоднородность образцов керна в объеме. Применение КТ, несмотря на современность и технологичность, имеет ряд проблем, связанных с разрешающей способностью метода для оценки неоднородности горной породы в области малых по физическому размеру неоднородностей (мелких пор), то есть микропористости.

С целью приведения оценок пористости, определяемых разными методами, к единым величинам, в работе проведен статистический анализ значений коэффициентов пористости, полученных по стандартным лабораторным петрофизическим исследованиям образцов керна и по результатам КТ керна.

Целью работы является разработка статистических моделей для оценки расхождения определения коэффициента пористости по КТ с более достоверными данными лабораторной петрофизики для терригенных и карбонатных горных пород. Оценка данного расхождения позволит оценивать долю микропористости в компьютерных 3D-моделях керна по результатам КТ. Рассмотрение терригенных и карбонатных пород раздельно связано с существенными отличиями минерального состава, структурно-текстурных особенностей отложений, структуры порового пространства этих двух основных литологических типов осадочных горных пород.

Задачи исследования включают:

• оценку влияния литологического состава пород на оценку K_п разными методами (петрофизика и КТ);
• оценку влияния диапазона варьирования K_п на сходимость результатов двух методов (петрофизика и КТ) для разных литологических типов пород;
• построение моделей для корректировки значений K_п по результатам КТ для разных литологических типов пород.

Решение данных задач основывается на проведении детального статистического анализа.

Теория

Существует два типа стандартных способов определения коэффициента пористости, широко применяемых в петрофизической практике, которые различаются по применяемой фазе: определение пористости жидкостенасыщением и определение пористости по газу (газоволюметрия). Данные способы измеряют не весь объем пор, а лишь те поры, которые связаны с поверхностью образца и между собой, составляющие, по классификации [12], открытую пористость. При этом использование жидкости либо газа позволяет заполнить их и с достаточной степенью точности измерить весь объем этих открытых и связанных пор. Разумеется, имеется также и способ, измеряющий полную и закрытую пористость (оценка К_п через минералогическую плотность), однако он применяется реже, поскольку требует разрушения образцов [13].

Вместе с тем в последние годы все большее распространение в практике петрофизических исследований получает сравнительно новый метод изучения порового пространства – компьютерная рентгеновская томография. Данный метод позволяет визуализировать поровое пространство внутри образца, что дает возможность качественно оценить пористость и установить взаимосвязь между ее распределением и литологической характеристикой исследуемого образца. При этом главным недостатком применения метода рентгеновской компьютерной томографии в стандартном петрофизическом комплексе исследований является низкая разрешающая способность. Данный метод позволяет визуализировать лишь поры, имеющие размеры до первых микрон, что приводит к существенной недооценке объема порового пространства, в результате чего коэффициент пористости, рассчитанный с помощью метода рентгеновской томографии, получается меньше, чем измеренный стандартными методами жидкостенасыщения и газоволюметрии.

Можно предположить, что степень близости значений коэффициентов пористости, рассчитанных по методам газоволюметрии-жидкостенасыщения и методу рентгеновской томографии, будет существенно зависеть от доминирующих размеров и количественного соотношения отдельных типов пор в исследуемом образце керна: открытых и закрытых, связанных и изолированных, крупных и мелких. По мнению авторов данной статьи, в основном это будет определяться литологическим составом образцов. Среди исследуемых типов горных пород-коллекторов структура порового пространства будет наиболее сильно отличаться для карбонатных и терригенных пород.

Для карбонатных коллекторов, как известно, характерна крайне неоднородная структура порового пространства, представленная и межзерновыми, и внутриформенными порами, кавернами и трещинами. Зачастую в некоторых типах карбонатных коллекторов, например, в известняках структурного типа грейнстоунов [14], большая часть емкостного пространства может быть представлена крупными кавернами и трещинами, что делает его хорошо визуализируемым с помощью метода рентгеновской томографии. Вместе с тем характер структуры емкостного пространства карбонатов не исключает наличия в образце некоторой доли закрытых пор, которые могут быть не обнаружены методами газоволюметрии и жидкостенасыщения, способных измерять только открытую пористость. Поэтому можно ожидать, что коэффициенты пористости карбонатных пород, определенные стандартными методами и методом рентгеновской томографии, могут быть близки по значениям друг к другу, но при этом быть сложены различными объемами.

Емкостное пространство терригенных пород-коллекторов характеризуется большей однородностью и степенью связности в силу преимущественно межзернового характера. Породы подобного состава образуют коллекторы гранулярного типа, близко описываемые моделью Слихтера, проницаемость в которой определяется пористостью и диаметром частиц [15]. Вместе с тем размеры отдельных элементов пустотного пространства этого типа пород обладают размерами, находящимися ниже границы разрешающей способности метода рентгеновской томографии. При этом, стоит отметить, что, несмотря на существование высокоразрешающих методов микро- и нанотомографии, данные методы возможно использовать лишь для отдельно изготовленных образцов миллиметровых размеров, как показано в работе [16], что исключает сравнение с определением коэффициента пористости с помощью стандартных методов, проводимых на цилиндрических образцах стандартным диаметром 30 или 25 мм.

Таким образом, в данной работе проводится сравнение оценок коэффициентов пористости, полученных разными методами на одних и тех же образцах стандартного размера карбонатного и терригенного состава.

Материалы и методы

Исследуемые образцы керна нефтяных месторождений Пермского края представлены выпиленными из полноразмерного керна цилиндрами стандартного диаметра и высотой 30 мм. Образцы относились к двум литологическим группам пород: терригенным и карбонатным.

Терригенные образцы представлены преимущественно песчаниками, алевритистыми песчаниками по составу кварцевыми и полевошпатово-кварцевыми; серыми, темно-серыми, бурыми и коричневыми; мелкозернистыми, среднемелкозернистыми и крупнозернистыми; разной степени сортированности; конформные либо цементированные глинистым, кальцитовым или железистым цементом; крепкие либо средней крепости, с минеральными включениями слюд, рудных минералов, пирита.

Карбонатные образцы представлены известняками, доломитами и доломитизироваными известняками светло-серыми, серыми, темно-серыми; органогенными, детритовыми, органогенно-детритовыми, комковато-детритовыми, комковато-водорослевыми, водорослевыми; иногда слабоглинистыми и глинистыми; пористыми, пористо-кавернозными и кавернозными; крепкими с частым присутствием стилолитовых швов и трещин, иногда выполненных кристаллами кальцита.

Для выполнения исследования проводилось измерение пористости газоволюметрическим методом (K_п, %) и с помощью метода рентгеновской компьютерной томографии (K_п^т, %).

Газоволюметрический метод выбран авторами по нескольким причинам: во-первых, данный метод является достаточно быстрым (на измерение одного образца в среднем требуется не более часа) и сравнительно простым и, как следствие, он наиболее часто применяется в петрофизических лабораториях; во-вторых, использование химически инертного газа вместо жидкости позволяет гарантированно исключить изменение образцов, вызванное, например, случайным нарушением технологии промывания и сушки образца после эксперимента по насыщению либо химического взаимодействия между жидкостью и минеральным скелетом образца.

Измерения пористости выполнялись на автоматизированном порозиметре-пермеаметре AP-608 (Coretest Systems, США). Принцип действия данной установки осуществляется методом нестационарной фильтрации [17].

Суть метода заключается в измерении порового объема с использованием принципа расширения гелия по закону Бойля, который гласит, что давление P какого-либо идеального газа, умноженное на его объем V, дает постоянное значение при постоянной температуре. Применительно к анализу керна закон Бойля заключается в способности определять неизвестный объем по расширению газа с известными значениями давления и температуры в пустое пространство и в использовании полученного давления для расчета неизвестного объема. Следовательно, зная P₁, P₂ и V₂, можно рассчитать V₁:

V₁ = (P₂·V₂)/P₁. (1)

При этом в порозиметре-пермеаметре АР-608 закачка гелия осуществляется с обоих концов образца. Диапазон проницаемости образцов, доступных для измерения на данной установке, составляет от 0,001 мД (породы с подобной проницаемостью не относятся к коллекторам) до 5000 мД. Соответственно, измеряемый диапазон пористости составляет от 0,1 до 40 %, что также перекрывает диапазоны, свойственные терригенным и карбонатным коллекторам.

Методика подготовки и измерения образцов соответствует ГОСТ¹ и заключалась в предварительном высушивании тщательно экстрагированных в спиртобензольной смеси образцов с помощью сушильного шкафа. Время и температура сушки образцов составляли не менее 8 ч и 105 ºС для карбонатных пород и не менее 12 ч и 80 ºС для терригенных пород. После сушки образцы остужались в эксикаторе, их геометрические характеристики измерялись с помощью электронного штангенциркуля, а далее проводилось определение коэффициента пористости с помощью установки АР-608. Все измерения проводились не менее пяти раз, по результатам всех пяти измерений рассчитывалось среднее арифметическое, которое и является определенным значением для каждого образца.

Вторым анализируемым в статье методом является компьютерная рентгеновская томография керна. Метод был разработан А. Кормаком и Г. Хаунсфилдом [18] и основан на преобразованиях Радона [19]. Суть метода заключается в создании серии рентгеновских снимков, получаемых при прохождении рентгеновского излучения через вращающийся вдоль одной оси образец. Полученные рентгеновские снимки преобразуются через обратное преобразование интеграла от функции прямой, направленной перпендикулярно вектору, который направлен вдоль направления излучения на определенном и измеренном вдоль него расстоянии.

В нашем исследовании для проведения рентгеновской томографии применялась система рентгеновского контроля с функцией компьютерной томографии Nikon XT H 225 (Nikon Metrology, Великобритания). Данная система имеет конструкцию, состоящую из стационарного источника рентгеновского излучения, образующего фокальное пятно размером 3 мкм, трехпозиционного вращающегося столика и детектора 2048×1408 пк, с физическим размером пикселя 142 мкм. Система позволяет изучать образцы стандартного диаметра 30 мм с разрешением до 20 мкм.

Съемка образцов проводилась на напряжениях источника излучения от 150 до 180 кВ, силе тока от 100 до 150 мА, с применением медного фильтра толщиной 0,5 мм, экспозиции 0,5 с, количеством снимков не менее 3000. Все образцы располагались так, чтобы разрешение получаемой реконструкции составляло не менее 25 мкм. Неоднородности размером менее 1 вокселя (25 мкм) относятся к так называемой микропористости, которую, в отличие от более крупной макропористости, невозможно различить с высокой точностью и напрямую геометрически выделить в образце. На практике для выделения такой пористости в образцах применяют ряд допущений. Например, о том, что микропоры располагаются по поверхности крупных пор, или микропоры могут быть локализованы в областях контакта зерен минералов, или же они распределены достаточно равномерно по объему минерального скелета. Однако для всех этих допущений необходимо оценивать долю этой микропористости.

Реконструкция объемного изображения производилась с помощью проприетарного программного обеспечения CT Pro 3D (Nikon Metrology, Великобритания), использующего для процедуры реконструкции усовершенствованную версию одного из наиболее распространенных алгоритмов FDK [20]. Реконструированные изображения обрабатывались в программе Avizo Fire (Visualization Science Group, Франция).

Методика обработки изображений образцов с целью получения объема порового пространства проводилась следующим образом. В исходной реконструкции – 32-битном черно-белом трехмерном изображении, где наиболее светлые участки соответствуют областям максимальной плотности (минеральному скелету), а наиболее темные – пустотному пространству, – была выполнена процедура бинаризации. Суть процедуры бинаризации заключается в том, что весь диапазон оттенков серого разделяется на два объема со значениями 0 и 1, соответствующими объемам пор и скелета (рис. 1).

Рис. 1. Выделение на фрагменте черно-белого изображения горной породы:
A – реконструированное изображение сечения образца в оттенках серого, пропорционального поглощению материала (черный – не поглощает, белый – поглощает);
В – выделение на фрагменте черно-белого изображения горной породы пустотного пространства (черный – воздух в порах и вокруг образца; белый – минеральный скелет)

Данные объемы, в свою очередь, уже могут быть измерены программными инструментами.

Расчет коэффициента пористости образца по томографии K_п^т производился с помощью стандартной формулы расчета пористости:

K_п^т = V_por/V_vol · 100, (2)

где V_por – объем бинаризованной модели порового пространства образца, мм³; V_vol – объем бинаризованной модели всего пространства образца, мм³.

¹ ГОСТ 26450.0-85–ГОСТ 26450.2-85. Породы горные. Методы определения коллекторских свойств. М.: Издательство стандартов; 1985. 16 с.

Результаты и анализ полученных данных

В данной части рассмотрены вопросы статистического анализа значений коэффициентов пористости, полученных описанными выше способами. На рис. 2 приведено сопоставление значений коэффициентов пористости, полученных газоволюметрическим методом (K_п, %) и методом рентгеновской томографии (K_п^т, %), для терригенных и карбонатных пород.

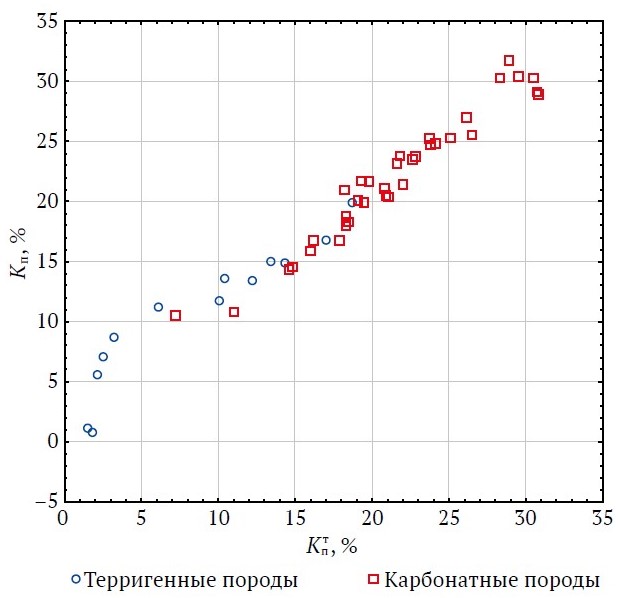
Рис. 2. Поля корреляции между K_п и K_п^т для различных пород

Для терригенных пород средние значения пористости для K_п^т и K_п равны 8,71 и 10,76 % соответственно при среднеквадратических отклонениях 6,17 и 5,82 %.

Для карбонатных пород средние значения пористости для K_п^т и K_п равны 21,43 и 22,00 % соответственно при среднеквадратических отклонениях 5,51 и 5,43 %.

Анализ приведенных корреляционных полей показывает, что соотношения значений K_п и K_п^т для изучаемых пород располагаются в различных диапазонах. Для терригенных пород значения K_п и K_п^т более низкие, чем для карбонатных. Сравнения средних значений по K_п и K_п^т для изучаемых пород выполнены по t-критерию Стьюдента и приведены в табл. 1.

Таблица 1

Сравнение средних значений K_п и K_п^т для различных типов пород

Отсюда видно, что средние значения коэффициентов пористости, определенные разными методами, статистически не различаются (достигаемый уровень значимости p > 0,05). При этом визуальный анализ корреляционных полей между K_п и K_п^т как для терригенных, так и для карбонатных пород показывает, что в пределах корреляционных полей наблюдаются различные соотношения в зависимости от значений K_п и K_п^т. В целом результаты оценки средних K_п и K_п^т статистически не противоречат друг другу, однако требуют более детального рассмотрения по диапазонам пористости. При этом средние значения по КТ всегда ниже, несмотря на разную литологию, что указывает на сложности и некоторую недооценку K_п для микропористости в силу физических ограничений метода КТ.

Для установления различных соотношений между K_п и K_п^т дифференцированно, в зависимости от литологии и диапазона K_п, расположим значения K_п образцов по возрастанию, где их количество увеличивалось на один (n = 3, n = 4, n = 5, …, n = 33 для карбонатных и n = 13 для терригенных пород). Общее количество рассматриваемых моделей определяется объемом выборки. Для каждого рассматриваемого диапазона значений K_п по n значениям проведем регрессионный анализ K_п = f(K_п^т) c оценкой парного коэффициента корреляции r и статистических характеристик коэффициентов уравнений регрессий.

Уравнение регрессии имеет следующий вид:

K_п = b + k∙K_п^т, (3)

где K_п – значения коэффициента пористости, полученные газоволюметрическим методом, %; K_п^т – значения коэффициента пористости, полученные методом рентгеновской томографии, %; b – свободный член в уравнении регрессии; k – угловой коэффициент в уравнении регрессии.

Для карбонатных пород параметры уравнений регрессии приведены в табл. 2.

Таблица 2

Уравнения регрессии зависимостей K_п от K_п^т (карбонатные породы)

* – статистически значимые значения (p ≤ 0,05).

Для карбонатных пород было построено 33 уравнения регрессии, значения коэффициента корреляции r изменялись от 0,892 до 0,975.

По статистическим характеристикам разработанных моделей построены зависимости изменения значений свободных членов уравнений регрессий, угловых коэффициентов при K_п^т и значений коэффициентов корреляции r (рис. 3–5).

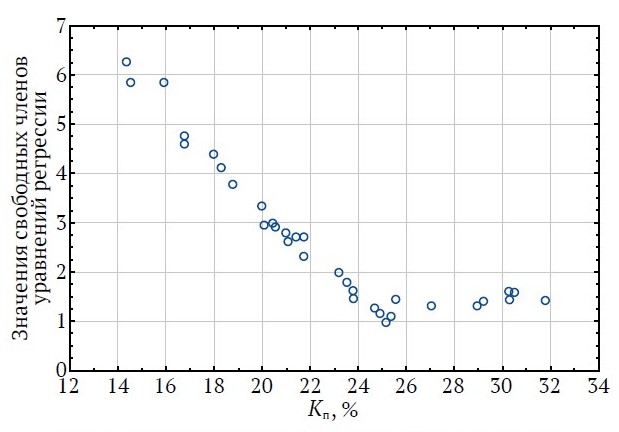
Рис. 3. Изменения значений свободных членов уравнений регрессии в зависимости от K_п (карбонатные породы)

Анализ показывает, что соотношения между изучаемыми величинами характеризуются двумя видами: при K_п < 24 %, при увеличении диапазона K_п происходит закономерное уменьшение свободных членов; при ещё большем увеличении K_п значения свободных членов изменяются незначительно.

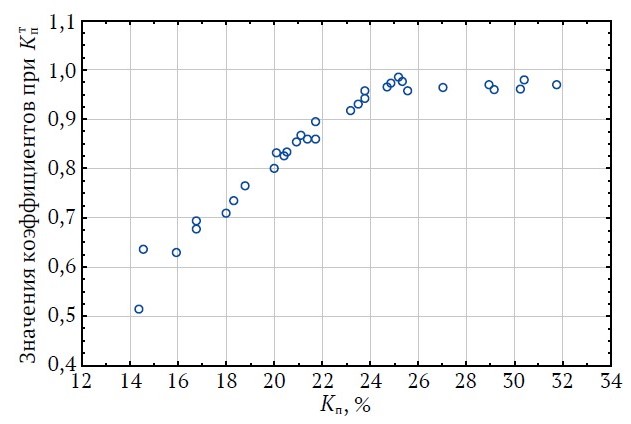
Рис. 4. Изменения значений угловых коэффициентов при K_п^т в уравнениях регрессии в зависимости от K_п (карбонатные породы)

Результаты свидетельствуют, что соотношения между изучаемыми величинами также характеризуются двумя видами: при K_п < 24 %, при повышении K_п происходит закономерное повышение коэффициентов при K_п^т; при ещё большем увеличении K_п значения коэффициентов изменяются незначительно и находятся в диапазоне 0,97–0,98.

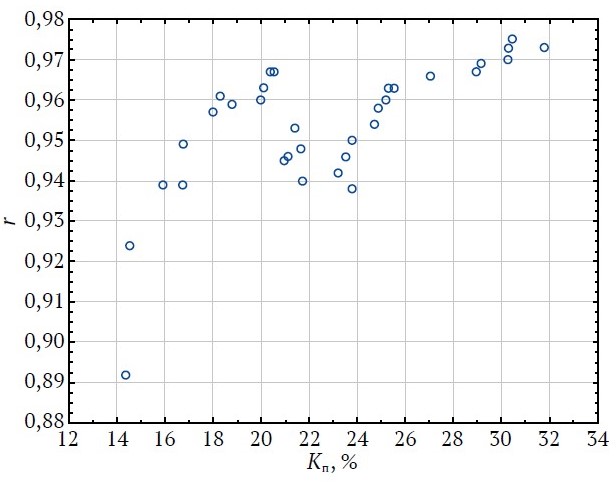
Рис. 5. Изменения значений коэффициентов корреляции r в зависимости от K_п (карбонатные породы)

Отсюда видно, что соотношения между изучаемыми величинами также характеризуются двумя видами: при K_п < 22 %, при повышении K_п происходит первоначально повышение значений r. При K_п < 23 % наблюдается снижение r. При ещё большем увеличении диапазона K_п значения коэффициентов повышаются по сложной траектории.

Вышеприведенный анализ зависимостей K_п и K_п^т в карбонатных породах показал, что представляется возможным выделить две границы, дифференцирующие величины K_п^т на три группы: первая – при K_п^т < 16,0 %; вторая – при 16,0 % ≤ K_п^т < 22,6%; третья – при K_п^т ≥ 22,6 %

Первая группа при K_п^т < 16,0 %, в которой зависимость K_п от K_п^т является статистически незначимой. При K_п^т от 16,0 до 22,6% наблюдаются статистически значимые корреляции между изучаемыми величинами. Для определения значений K_п от K_п^т необходимо производить корректировку, используя уравнение регрессии, приведенное в табл. 4. При K_п^т ≥ 22,6% также нужно проводить корректировку значений по формуле, приведенной в табл. 3.

Таблица 3

Уравнения регрессии зависимостей K_п от K_п^т (карбонатные породы)

Таким образом, выполненные исследования показывают, что значения K_п^т, полученные методом рентгеновской томографии для карбонатных пород, несмотря на статистическое равенство средних значений, характеризуются различными статистическими связями. При K_п^т < 16,0% наблюдается отсутствие значимой корреляционной связи с K_п. Это свидетельствует о том, что по данным методам получаем различные значения коэффициентов пористости. При K_п^т ≥ 16,0 % значения K_п^т и K_п статистически контролируют друг друга. При этом необходимо отметить, что на определенных интервалах значений величины свободных членов являются статистически значимыми. Это свидетельствует о том, что наблюдается корректировка значений K_п свободными членами уравнений регрессии. Поэтому для корректного использования величин K_п^т и K_п в карбонатных породах необходимо использование полученных уравнений регрессии для диапазонов K_п.

Аналогичный анализ выполнен и для терригенных пород (табл. 4).

Таблица 4

Уравнения регрессии зависимостей K_п от K_п^т (терригенные породы)

* – статистически значимые значения (p ≤ 0,05).

Для терригенных пород было построено 11 уравнений регрессии, значения r изменялись от 0,806 до 0,937. Анализ свободных членов уравнений регрессии показывает, что при K_п^т < 11,75 % наблюдается изменение их от отрицательных к положительным значениям. Значения угловых коэффициентов при K_п^т также характеризуются закономерным изменением от высоких значений (больше 1) к низким (меньше 1). Изменения значений коэффициентов корреляции r приведены на рис. 6.

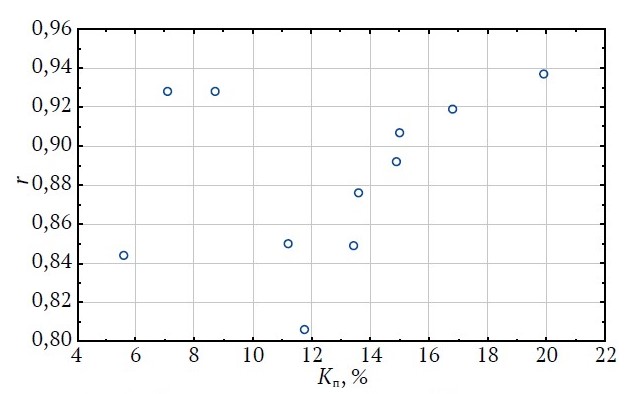
Рис. 6. Изменения значений коэффициентов корреляции r в зависимости от K_п (терригенные породы)

Анализ показывает, что соотношения между изучаемыми величинами также характеризуются двумя видами: при K_п < 12 %, при повышении K_п происходит хаотичное изменение значений r; при увеличении диапазона K_п происходит закономерное повышение значений от 0,849 до 0,937.

Анализ построенных уравнений регрессии показал, что при K_п^т ≤ 7,1 % зависимость K_п от K_п^т является статистически незначимой. При K_п^т > 7,1 % получено статистически значимое уравнение регрессии:

K_п = 6,349+0,63905K_п^т, при r = 0,964, p = 0,00002. (4)

Это свидетельствует о том, что соотношения между K_п и K_п^т характеризуются наличием статистической связи.

Практическое применение и направление дальнейших исследований

Таким образом, выполненные исследования показывают, что данные методы не заменяют, а дополняют друг друга, поскольку обладают различающимися ограничениями в применении. Вместе с тем проведенный статистический анализ показал, что использование обоих методов дает естественным образом отличающиеся, но статистически связанные результаты, что демонстрирует возможность их совместного применения. Важно также то, что при исследованиях образцов различных литологических типов коллекторов методы имеют различные ограничения:

1) при исследованиях карбонатных образцов оба метода показывают статистически значимые коэффициенты корреляции между K_п и K_п^т при значениях K_п по газоволюметрическому методу более 16%, что может объясняться более крупными размерами пустот;

2) при исследованиях терригенных образцов пористость наиболее точно определяется при значениях пористости K_п более 7,1 %, что может быть связано со слабым заполнением межзерновых пустот цементом или хорошей сортированностью материала.

Применение рекомендуемых уравнений для литотипов по диапазонам K_п позволяет получать интегральную оценку микропористости как разность между оценкой K_п по уравнению и значением K_п^т по данным КТ. Особенно это применимо к образцам неправильной или сложной формы, которые не всегда возможно полноценно исследовать в петрофизической лаборатории. Такая интегральная оценка микропористости позволяет получить ограничение на суммарный объем распределяемых микропор, что повысит качество объемных компьютерных моделей керна и порового пространства пород-коллекторов.

Результаты исследования могут быть использованы при петрофизическом обосновании фильтрационно-емкостных свойств пород-коллекторов месторождений нефти и газа.

Использование предлагаемого подхода позволяет повысить качество 3D-моделей керна горных пород, что в конечном итоге приведет к повышению точности различных методов моделирования, связанных со свойствами горных пород, и позволит более рационально и c наибольшей экономической эффективностью разрабатывать месторождения нефти и газа (или других полезных ископаемых).

Дальнейшие направления исследований представляются авторам в продолжении экспериментов при увеличении количества и разнообразия образцов, что позволит уточнить полученные зависимости, а также в учете дополнительных стандартных характеристик керна (значение коэффициента остаточной нефтенасыщенности, капиллярные кривые и др.).

Заключение

Выполненные исследования убедительно показывают, что при комплексном использовании данных по коэффициентам пористости, полученных разными способами как для карбонатных, так и для терригенных пород, полученные результаты должны сопоставляться.

Результаты оценки средних между K_п и K_п^т по терригенным и карбонатным породам статистически не противоречат друг другу. При этом средние значения по КТ всегда ниже, несмотря на разную литологию, что указывает на сложности и некоторую недооценку К_п для микропористости, в силу физических ограничений и особенностей метода КТ.

Выполненные исследования показывают, что значения K_п и K_п^т, полученные методом рентгеновской томографии для карбонатных пород, при K_п^т < 16,0 % не имеют связи с K_п. Для значений вне этого диапазона предложены уравнения оценки и корректировки значений K_п.

Анализ построенных уравнений регрессии для терригенных пород показал, что при K_п^т ≤ 7,1 % зависимость K_п от K_п^т является статистически незначимой. Для значений вне этого диапазона предложены уравнения для оценки и корректировки значений K_п.

Применение рекомендуемых уравнений для литотипов по диапазонам K_п позволяет получать интегральную оценку микропористости как разность между оценкой K_п по уравнению и значением K_п^т по данным КТ. Предлагаемые подходы позволяют повысить качество объемных 3D-моделей структуры порового пространства горных пород.