Fracture toughness of rock-concrete interfaces and its prediction based on acoustic properties

Introduction

In current mining activities, the study subject is often the interface between rock and concrete taking place in many surface and underground structures such as mine shafts, hydroelectric dams in mountainous areas, reinforced concrete tunnel support and other similar facilities. One of the tasks in the construction and operation of such structures is to ensure their safety and prevent failure under the effect of both static loads from overlying rocks and soils and dynamic impacts. The sources of dynamic impacts are seismic waves from explosions [1] and earthquakes [2, 3]. The subject under consideration is an integral part of the solution of the above problem and requires experimental studies (testing) of the strength properties of the interface between rock and concrete.

The theoretical justification of the studies described below is based on the fundamental works of A. Griffiths [4]. Within this theory stress intensity factor K is considered [5]. Under tension, the stress intensity factor of the first strain mode , where σ is the effective stress, l is fracture length. The ability of a material to maintain its integrity is evaluated by the corresponding fracture toughness coefficient (FT) K_IC, determined based on experimental data. It is a characteristic of a fractured material and characterizes the maximum length of a fracture at which no fracture germination occurs. The condition of absence of fracture growth and subsequent failure is described by the expression K_I ≤ K_IC.

Knowing the effective stresses σ, as well as FT in combination with the parameters of fractured rock masses and concrete supports will allow ensuring their safety in the design, construction, and operation of mining facilities under the conditions of static and dynamic loads.

FT is applicable to both separate materials such as metals, concrete, composites, and the interfaces between them. Many researchers have studied FT for metals and alloys [6, 7], including heterogeneous ones [8]. For composite materials, FT was investigated in [9, 10]. FT is also used in the evaluation of strength properties of concrete [11], including for special types of concrete such as fibre concrete [12]. FT was used for novel materials used for manufacturing articles at printers [13]. Far fewer publications are devoted to rock FT studies [14], especially concrete-rock interfaces [15].

Typically, experimental research techniques use three- or four-point bending loading schemes for specimens and rectangular beams [16, 17], half-disks [18], disk specimens [19], and cubes with a notch [20]. For rocks, the FT determination methodology recommended by the International Society of Rock Mechanics (ISRM) is used [21]. FT of interfaces between different rocks or minerals is also of interest in assessing the stability of rock masses. In [22, 23], the methodology and results of determining the  fracture toughness coefficient with respect to the interfaces between different  rock types was described, and the FT ranges  for some their combinations were determined.

The purpose as well as the novelty of this paper consists in evaluating FT of the first strain mode K_IC of the interfaces between different rock types and concrete. In addition, the acoustic properties of rock specimens were determined, and their relationship with K_IC was evaluated. These properties included longitudinal and transverse elastic wave velocities, as well as internal mechanical loss factor Q⁻¹ [24, 25] to evaluate the feasibility of predicting K_IC based on the data of acoustic measurements.

The tasks addressed included:

• Justification of the testing technique for determining FT of rock-concrete interfaces;
• Determination of elastic wave propagation velocities by ultrasonic pulse scanning before and after a test to assess the effect of a forming fracture on the velocities;
• Determination of loss factor Q⁻¹ and its changes during the formation of a reference fracture by the resonance method;
• ISRM bending testing of specimens to determine the K_IC of rock-concrete interfaces;
• Processing and comparative analysis of the obtained results with determining the ranges of FT values for the interfaces between rocks of different types, as well as between rocks and concrete;
• Practical conclusions on the obtained FT values of the interfaces between rocks of different types and concrete to be taken into account in the design and operation of structural elements of mining systems at mining enterprises.

1. Research Materials and Techniques

For testing, cylinder specimens 40 mm in diameter and 150 mm long were produced, consisting of two equal parts: rocks from the Novomoskovsk gypsum deposit (Novomoskovsk, Tula region, Russia) [22, 23] and sand-cement mortar. A series of 19 such specimens was prepared and aged for four months until the mortar was fully cured (Fig. 1, a). In addition, four specimens were made entirely of sand-cement mortar (Fig. 1, b). V-shaped notches were cut in the specimens for the ISRM testing described below.

Fig. 1. Specimens with gypsum stone – cement stone interfaces (a) and cement stone specimens with notches (b)

The test specimens were labeled according to the original 150 mm long gypsum specimens, half of which were used to make concrete coated specimens C. They were labeled as:

• GGC gypsum stone;
• gypsum stone and GKC flintstone interfaces;
• KKC flintstone;
• gypsum-flintstone interface with veins of carbonaceous GUKC clays.

For example, GKC3-1 meant a specimen with an interface between concrete and half of the number 1 specimen made of gypsum and flintstone GK-3.

Tests on 150 mm long cylindrical specimens with notches were carried out according to the three-point scheme shown in Fig. 2, a. The notch was V-shaped, Fig. 2, b, and the angle θ was 90°.

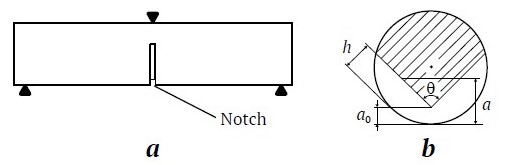
Fig. 2. Schematic of a three-point test on a notched specimen (a) and cross-section of a notched specimen (b)

In the calculations, formula (1) from [21] was used to determine the fracture toughness coefficient:

K_IC = A_minP_max/D^1.5, A_min = [1.835+7.15a₀/D+9.85(a₀/D)²]S/D,                  (1)

where K_IC is fracture toughness coefficient, MPa×√m; P_max is maximum bending force, kN; D is diameter of a chevron bending of specimen, cm; a₀ is distance between the chevron indents and specimen surface, cm; S is distance between the support points, cm.

During the tests, an installation based on the ASIS complex (NPO Geotech LLC, Penza, Russia) was used. The specimens were tested using a three-point bending pattern. In addition to the system that set the cyclic motion of the frame, a second system was used to record the deflection force and magnitude. Two linear displacement transducers (LVDTs) with a measurement range of 10 mm recorded deflection directly on a specimen. These transducers were connected to the 18-bit ADC of the QMBox measuring system (R-Technology, Moscow, Russia).

The installation for determining internal mechanical losses included a JDS 2900 series signal generator with a DPA 1698 power amplifier, a GDS-71022 oscillograph with an external preamplifier, and a specimen holder. Piezoelectric transducers 1.2 mm thick were glued to the ends of a specimen to measure the acoustic losses using the resonance method.

Longitudinal P- and transverse S-wave velocities were measured using an ultrasonic instrument (Ecogeos Prom LLC, Tver, Russia). The velocities were determined based on the time taken by elastic pulses to travel through the specimens.

Cycle tests involved maximum frame displacements of 0.10, 0.15, 0.20, 0.25, 0.30, 0.35, 0.40 mm. The minimum displacement was 0.05 mm. The displacement speed was 0.2 mm/min.

Acoustic tests along the long axis of the specimens included the measurement of propagation velocities of longitudinal V_p and transverse V_s elastic waves in a rock using standard techniques. Internal mechanical losses were estimated based on the loss factor (or inverse Q-factor) Q⁻¹. These estimates were carried out in addition to the mechanical tests two times, before and after a specimen was tested.

Experimental Q⁻¹ measurements were performed through frequency scanning of the resonance characteristics of a specimen. The signal from the SFG-2110 harmonic oscillator was applied to an exciting piezoceramic plate 20.0 mm in diameter and 1.5 mm thick, which was mounted at one end of a specimen. From a second similar piezoelectric plate at the opposite end of the specimen, the signal was fed to a preamplifier with a bandwidth of 20-500 kHz and then to a GDS-71022 digital oscillograph. The Q⁻¹ factor was calculated using the following formula:

Q⁻¹ = Δf/f,                                                            (2)

where Δf is frequency bandwidth at 1/√2 of the maximum of the resonance curve; f₀ is resonance frequency.

2. Testing results

2.1. K_IC coefficient measurement results for rock-concrete specimens

Figs. 3–6 show, for example, the curves of the time dependencies of a specimen load P and deflection y, as well as the load P dependence of deflection y. The complete set of plots for all 19 specimens with rock-concrete contacts and four concrete specimens are available in the data.mendeley.com repository [26].

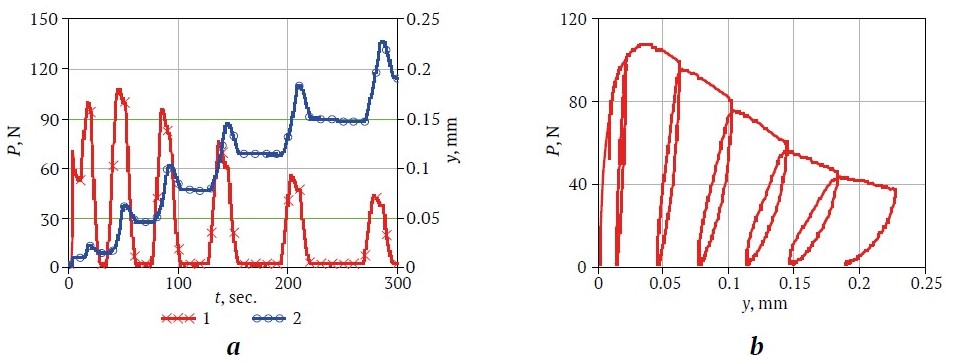
Fig. 3. Curves of time dependencies of load and deflection (a) load dependence of deflection (b) under cyclic loading of specimen GKC3-2

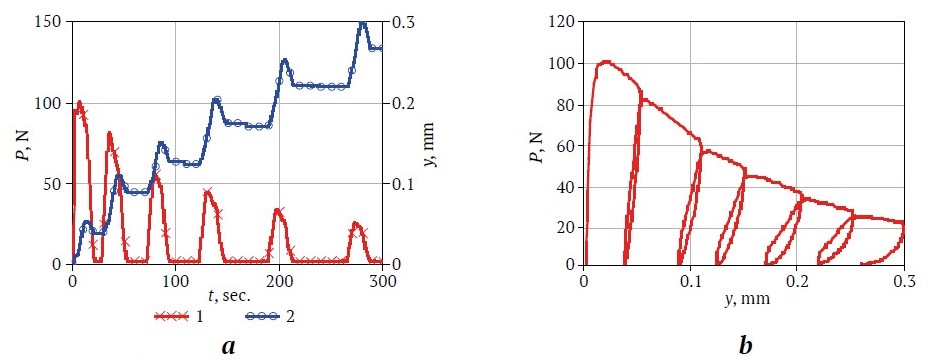
Fig. 4. Curves of time dependencies of load and deflection (a) and load dependence of deflection (b) under cyclic loading of specimen GKС5–1

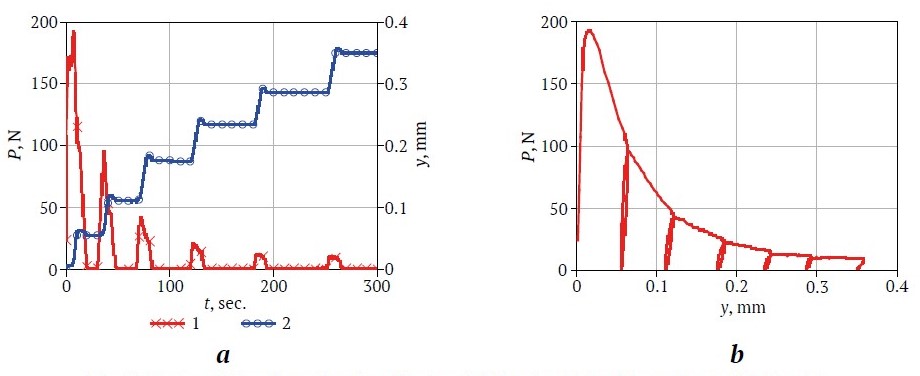
Fig. 5. Curves of time dependencies of load and deflection (a) and load dependence of deflection (b) under cyclic loading of specimen GKС5–2

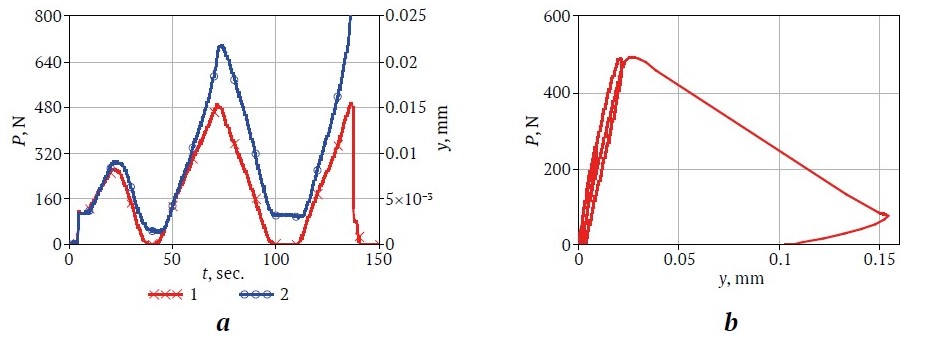
Fig. 6. Curves of time dependencies of load and deflection (a) and load dependence of deflection (b) under cyclic loading of specimen C1

2.2. Concrete specimens testing results

Fig. 6 shows similar test results for concrete specimens as an example.

2.3. Acoustic properties of specimens with rock-concrete interface

Tables 1 and 2 summarize the results of measuring K_IC using formula (1) and the acoustic properties of rock-concrete specimens and concrete specimens before and after testing. The following designations are used in the tables:

P_max is maximum load during cyclic loading of a specimen;

K_IC is fracturing toughness coefficient of the first mode of strain;

V_p is velocity of longitudinal wave propagation;

V_s is velocity of transverse wave propagation;

f₀ is specimen resonance frequency;

Q⁻¹ is internal mechanical loss factor.

In Table 1, dashes indicate specimens broken up during testing.

After testing, no clear resonance could be obtained in the specimens due to the increased losses in the concrete that is indicated by dashes in Table 2.

For comparison, Table 3 presents the data from previous tests on specimens of rocks and their interfaces without concrete.

Table 1

Properties of specimens with rock-concrete interface

Table  2

Properties of concrete specimens

Table  3

K_IC fracture toughness coefficients of rocks and contacts between them without concrete [22, 23]

3. Findings Discussion

Let us analyze the shapes of the curves in Fig. 3–6, obtained when testing specimens in the conditions of specified cyclic bending strains with increasing maximum displacements in each subsequent cycle.

The peculiarities of plastic strain of the specimens deserve attention. They consisted in the increase of residual plastic strains after each strain cycle and manifested themselves in the form of a characteristic loop-shaped pattern of curves P(y) with a shift to the right of each subsequent loop. The plots clearly show an area of extreme strain where the maximum load decreased with increasing number of cycles. Coefficient K_IC was calculated based on the highest maximum value P_max. For clarity, all the results of the K_IC testing are presented in the diagram in Fig. 7.

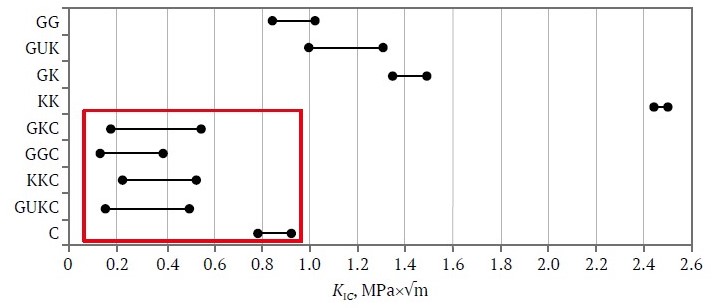
Fig. 7. Ranges of variation of K_IC coefficient for rocks, rock-concrete interfaces, and concrete (encircled)

The analysis of K_IC values given in Tables 1 and 3, as well as in Fig. 7, allows drawing the following conclusions.

Without concrete, the interfaces have relatively high K_IC values, especially KKs, for which the K_IC is greater than 2. The presence of flintstone is generally characterized by high K_IC values even in the presence of thin carbonaceous interlayers. The absence of flintstone, such as in the case of GG, is characterized by reduced K_IC values. For pure concrete, K_IC has values close to those for the GG interfaces. For rock-concrete interfaces, K_IC values are extremely low. This can be explained by weak adhesion when forming the contact between them. The difference is especially evident when comparing the averages. The average K_IC value for the specimens without concrete is 1.327 MPa×√m, the average value for concrete is 0.858 MPa×√m, and for the specimens with concrete it was 0.323 MPa×√m, which is 4 times less than that for the specimens without concrete and 2.5 times less than that for the concrete specimens.

As follows from the data of summary Table 1, in most cases, the appearance of a fracture in a specimen middle part in bending tests leads to a decrease in both velocity V_p and velocity V_s. The changes were considered to be significant if they were beyond ±2% of the original pre-test value. The proportion of specimens whose velocity V_p appeared unchanged, amounted to 42%, and that whose velocity V_s remained unchangable, 40%. At the same time, half of the specimens showed a decrease in V_p, while V_s showed both decrease and increase in equal proportions. F₀ и Q⁻¹ showed a change in all cases.

Quantification of the changes in the mean values of V_p and V_s shows insignificant decreases, they amounted to 0.992 and 0.964 of the initial values. However, such small changes may not be a sufficiently reliable result. At the same time, the average value of Q⁻¹ (loss factor) for a fracture formation due to a test showed an increase of 1.32 times that can be used to assess the condition of the interface between a rock and concrete when organizing nondestructive testing or monitoring of actual facilities.

Establishing the feasibility of predicting K_IC based on the acoustic properties of facilities is one of the important related objectives. In this case, such an assessment is made on the basis of the correlation coefficient R and root-mean-square deviation (RMS). The correlation coefficients of different combinations of acoustic properties with K_IC of the specimens with rock-concrete interfaces were calculated using Statistica software. The results are presented in Table 4.

As follows from these data, the highest interdependence of K_IC and V_p is observed.  When multivariate statistics is used, other properties allow the correlation coefficient to increase slightly. At the same time, even in this case at R = 0.685, although interdependence exists, it cannot be considered as very strong. Root-mean-square deviation RMS characterizes the accuracy of such a forecast. In this case, the root-mean-square deviation was 0.098 MPa×√m. The average value of K_IC was 0.323 MPa×√m. The relative accuracy was about 30%.

Table 4

The relationship between the velocities of elastic waves V_p, V_s, loss factor Q⁻¹ in different combinations and K_IC coefficient for specimens with rock-concrete interfaces

Conclusion

The relevance of the experimental study of a rock-concrete interface fracture toughness coefficient K_IC was shown, which can be used in practice in mining industry in the design, construction, and operation of surface and underground structures, such as shafts and permanent mine workings, hydroelectric dams, road and railroad tunnels, as well as other both underground and aboveground facilities having rock-concrete interface.

The current study investigated the fracture toughness of rock interfaces involving gypsum stone and concrete. For the rock-concrete interfaces, the values of the fracturing toughness coefficient of the first strain mode K_IC are extremely low. This can be explained by weak adhesion when forming the contact between them. The difference is especially evident when comparing the averages. The average K_IC value for the specimens without concrete is 1.327 MPa×√m, the average value for concrete is 0.858 MPa×√m, and that for specimens with concrete is 0.323 MPa×√m, which is 4 times less than that of the specimens without concrete and 2.5 times less than that of the concrete specimens.

Evaluation of the effect of an arising fracture on average values of longitudinal V_p and transverse V_s elastic wave velocities shows negligible reductions, which are 0.992 and 0.964 of the initial (pre-test) values, respectively. At the same time, the loss factor Q⁻¹ at the formation of a tensile fracture due to testing shows an increase of 1.32 times, which can be accepted as statistically significant.

An evaluation of the feasibility to predict K_IC coefficient based on the acoustic properties showed that the highest correlation was observed with V_p velocity. When multivariate statistics is used, other properties allow the correlation coefficient R to increase slightly. At the same time, even in this case at R = 0.685, the correlation cannot be qualified as strong, although the relationship exists. The relative accuracy in this case is 30%.

The obtained results can be used in the design, operation, as well as organization of nondestructive testing and monitoring of industrial facilities of mining enterprises.