Variation of ore grades in the boundary zone of subeconomic ore

Introduction

The overwhelming majority of deposits of non-ferrous, precious, and rare metals in Kazakhstan, as well as in other parts of the world, are characterized by complex structural organization [1–3]. Such deposits display a range of distinctive features: diversity of ore body morphology, significant variability in geometric parameters, intricate spatial distribution within the host rock mass, heterogeneity in the distribution of valuable components, and pronounced contrasts in the physical and mechanical properties of host rocks [4–6]. Together, these geological factors define the complexity of deposit sections with heterogeneous structure [7, 8]. Importantly, such deposits account for 60–90% of non-ferrous metal production in the CIS, while technologically unavoidable operational ore losses may reach 20–35% of total output [6, 9, 10].

Analysis shows that the main factors contributing to increased ore losses and dilution in open-pit mining of complex-structured deposits are:

• insufficient knowledge of the geological and morphological features of structurally heterogeneous bench blocks;
• mismatch between the applied mining technologies for excavation and haulage operations and the actual geological conditions of ore occurrence, both in situ and after drilling, blasting, and extraction.

Addressing these challenges requires the development of fundamentally new methods for assessing ore grades in boundary zones between economic and subeconomic ore. The adoption of such approaches would markedly improve the accuracy of quantitative and qualitative assessment of mined material and provide more effective control over ore losses and dilution. This line of research is highly relevant for the modern mining industry, yet a review of earlier studies shows that it has not been sufficiently addressed in the literature.

A comprehensive solution calls for a systems approach that integrates:

• advanced digital technologies and information systems;
• conventional methods for evaluating ore quality;
• reliable data on deposit geology and morphology.

Only such an integrative approach can ensure the required accuracy in assessing the quality of mined ore at every stage of deposit development.

As shown in [6, 9], the combined influence of mining-technical factors, geological structure, and mineral composition of a deposit determines not only the choice of mining method, but also ore preparation and beneficiation technologies. Ore losses and dilution, the primary negative factors reducing ore quality, largely depend on the adjustment of operational sampling methods, preliminary delineation of ore bodies, and strict compliance with boundaries during stoping operations [10]. Moreover, identifying types of complex-structured bench blocks, determining the ore saturation coefficient, and quantifying the structural complexity index serve as objective criteria for evaluating recovery [11]. Analytical relationships for calculating the grade of valuable components in shipped ore (α′) have also been proposed to substantiate complete extraction of ore from complex-structured bench blocks [12]. At the same time, particular attention should be given to evaluating and regulating the extraction of boundary zones, analyzing the influence of complex ore body geometries, and characterizing the morphology of these zones [13].

As previously substantiated, the most effective solution combines traditional research methods with advanced digital technologies. In recent years, computer modeling of deposit geology and the spatial distribution of ore bodies has become increasingly common in specialized studies. This is carried out using modern geological and mining information systems (GMIS), specialized software platforms for three-dimensional modeling and deposit analysis.

Of particular interest are studies in which the application of GMIS has led to the development and successful testing of innovative methods for assessing ore grades and quality parameters. For example, [5] describes the use of block modeling techniques that allow accurate determination of the spatial distribution of valuable components within ore bodies. This approach offers fundamentally new opportunities for analyzing deposit morphology and predicting ore grades. The block modeling methodology enables reliable zoning of technological ore types and grade categories within the open-pit space. Another method involves geometrical modeling of quality parameters in titanomagnetite deposits to construct wireframe models of ore bodies within closed outlines of mine workings, thereby distinguishing technological ore types [14]. Furthermore, it has been demonstrated that the delineation of geological domains with complex morphologies, together with quantitative evaluation of associated uncertainty, can be achieved through geostatistical modeling [15]. Boundary delineation methods based on these models may be used to refine and extend ore grade prediction techniques in boundary zones. Earlier research also proposed a neural-network-based method for delineating lithological differences for 3D modeling of ore bodies and host rocks, improving both the quality and speed of geological data processing at all stages of deposit development [16]. However, despite the clear advantages of modern computer models, limitations remain [17]. In particular, block models often lack precision in delineating ore bodies and may fail to accurately distinguish between economic and subeconomic ore.

The use of GMIS extends beyond deposit and ore body modeling; it is also an integral tool for ore flow quality management and monitoring. Studies [18, 19] highlight the importance of obtaining reliable data and forecasting ore grades across different parts of mined bench blocks for effective ore flow management based on a combination of segregation and blending principles. This approach has enabled a stable feed composition and optimal ore parameters for the beneficiation of low-grade apatite–nepheline ores [18] and copper–porphyry ores [19]. It has also been shown that determining ore grades at the boundaries and beyond the delineated limits of ore bodies is a critical task influencing both the quantity and quality of shipped ore. Enhancing the efficiency of mining and processing operations requires automated integration of extraction and beneficiation cycles, supported by information systems capable of handling tasks ranging from ore grade forecasting to real-time monitoring of ore flow quality and tonnage throughout the production process [20].

The reviewed studies highlight the importance of determining ore grades in boundary zones of subeconomic ore, in shipped ore, and in addressing ore losses and dilution during extraction. At the same time, determining ore grades in boundary zones requires targeted research aimed at maximizing recovery of economic ore through the selective incorporation of subeconomic material.

Objective: To establish variations in ore grades within the boundary zones of subeconomic ore based on borehole samples from several deposits of non-ferrous, precious, and rare metals in Kazakhstan.

Tasks:

1. To identify patterns of variation in valuable component grades with increasing distance from the boundary of economic ore at the Koktas-Sharykty, Kaskyrkazgan, Yuzhny-Mointy, and Naiman-Zhal deposits.
2. To determine the thickness of the admixed subeconomic ore layer in the boundary zone that ensures the required ore grades in shipped ore.
3. To establish new regularities in ore grades in shipped ore that guarantee production of concentrate of the required quality.

By controlling the thickness of the admixed subeconomic ore layer within limits that maintain the required ore quality for delivery to the concentrator, it is possible to reduce losses and increase the overall recovery of valuable minerals. To provide a scientific and technical basis for this concept, several real deposits in Kazakhstan are examined.

1. Selected deposits of non-ferrous, precious, and rare metals in Kazakhstan

1.1. The Yuzhny-Mointy area is located within the Northern Pribalkhash region, at the intersection of three major tectonic structures of regional scale: the Tokrau synclinorium, the Kyzyl-Esp anticlinal zone, and the Western Balkhash synclinorium. The territory is characterized by an exceptionally complex fold–block geological structure. A distinctive feature of the area is the combination of extensive zones of intensely deformed Riphean formations with localized occurrences of younger sedimentary strata belonging to the Silurian, Devonian, and Permian periods.

The geological structure of the area is complicated by numerous intrusive bodies, dominated by granitoid massifs of varying size and morphology. The primary bedding of the rocks is substantially disrupted by a well-developed system of tectonic faults, including both large regional faults of different orientations and numerous small-displacement faults. Collectively, these factors form a characteristic mosaic geological pattern across the study area.

Exploration and prospecting conducted in recent years have revealed important features of gold mineralization distribution. Studies have shown that nearly all identified vein zones and ore bodies are marked by extensive primary dispersion halos of gold. The surface width of these halos and their down-dip extent (at a cut-off grade of ≥ 0.01 g/t) in most cases exceed the length of the existing mine workings. This indicates that none of the trenches or boreholes completed so far has intersected the entire zone of low-grade gold mineralization.

Within the studied sites, economically significant ore bodies have been delineated, with thicknesses ranging from 0.1 to 14 m. Gold grades in individual samples vary widely – from 0.5 to 126.9 g/t – while average block grades across the deposit range from 1.38 to 9.73 g/t [21]. These results demonstrate the presence of promising areas with economic gold mineralization within the Yuzhny-Mointy area.

1.2. At the Koktas-Sharykty deposit, ore bodies with pronounced copper mineralization have been identified and studied in detail. A distinctive feature of their spatial position is their association with contact zones between coarse clastic sedimentary rocks of Givetian–Frasnian age and a subvolcanic massif of andesite porphyrites. Mineralization occurs both in the immediate vicinity of the contact and directly within the contact zone of these geological formations.

The ore bodies display a wide range of morphological characteristics. Lenticular and tabular forms are most common, although irregularly shaped bodies also occur (Fig. 1). A distinctive feature is the presence of numerous swellings and pinch-outs, reflecting the complex conditions under which the ore bodies formed. The spatial position of the mineralized zones is variable – they may be located either within the porphyrite massif or in the surrounding terrigenous rocks, composed mainly of conglomerates and, to a lesser extent, sandstones.

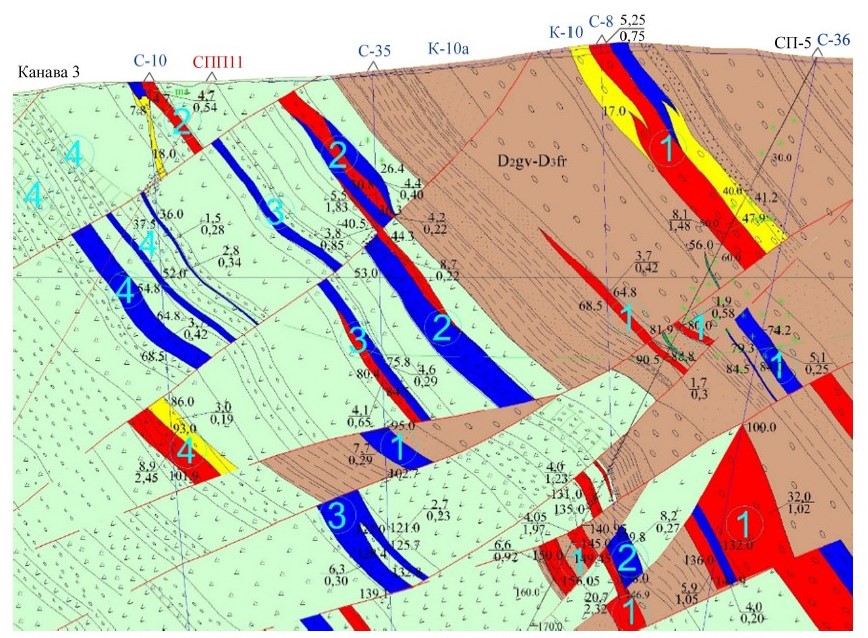
Fig. 1. Geological cross-section along profile III–III of the Koktas-Sharykty deposit

The exposed ore bodies are relatively small, with dimensions ranging from 10 × 2 to 160 × 120 m. Their spatial distribution is marked by the clustering of closely spaced bodies into four well-defined ore zones. All of these zones share a consistent northwest orientation (300–320°), which corresponds to the strike of both the andesite porphyrite body and the enclosing Givetian–Frasnian sedimentary rocks [22].

Detailed characteristics of the ore zones

First (southernmost) ore zone: Consists of two ore bodies measuring 10 × 2 m and 130 × 5–30 m. The first body lies directly within the bed of the Sharykty River. The second has a complex morphology, branching at its southeastern end where it gradually pinches out, while on the northwestern flank it dips beneath modern unconsolidated sediments.

Second ore zone: Located 60–70 m northeast of the first. It comprises five relatively small ore bodies that form a distinct chain about 120 m long. The largest body in this zone measures 50 × 10 m.

Third ore zone: Situated 40–50 m northeast of the second. Here, all ore bodies occur exclusively within the andesite–porphyrite massif. The zone is characterized by a discontinuous arrangement of bodies forming a chain with a total length of 440 m. The largest body reaches 120 × 20 m.

Fourth ore zone: Found 90–100 m northeast of the third. It includes two ore bodies measuring 160 × 15 m and 60 × 10 m. This is the northeasternmost of all the identified mineralized zones.

1.3. The Kaskyrkazgan copper–molybdenum deposit belongs to the Kaskyrkazgan group, which also includes the Kepcham and Kenkuduk porphyry copper deposits. Deposits of the Kaskyrkazgan group are located in the central part of the Tokrau intrusive–tectonic zone, characterized by a complex structure, with mineralization concentrated in the apical portion of a granite–porphyry stock enriched in xenoliths of host rocks.

In terms of composition, the ores at these deposits are complex copper–molybdenum types, divided into oxidized and primary sulfide zones.

The oxidized ores are poorly developed, extending to depths of up to 20 m and only rarely to 45 m. The main minerals are bornite, chalcocite, limonite, hematite, malachite, azurite, chrysocolla, cuprite, goethite, and hydrogoethite. Greater importance, however, is attached to the transition zone of mixed ores.

Copper–molybdenum mineralization is of disseminated–veinlet type within a granodiorite massif, typically associated with contacts containing xenoliths of sedimentary rocks and quartz porphyrites. Copper mineralization occurs mainly in disseminated form, whereas molybdenum mineralization is largely veinlet-type. The correlation between copper and molybdenum is weak: molybdenite veinlets often cut across zones of disseminated copper mineralization and in some cases extend well beyond them.

Overall, the deposit is marked by highly complex mineralization patterns. Ore intervals are usually interbedded with barren layers, with irregular thicknesses ranging from tens of meters to mere decimeters (Fig. 2). The disseminated mineralization is generally not massive but appears pockety, producing a “checkerboard” pattern in cross-sections – even between adjacent boreholes on the same exploration line. Dissemination of ore minerals observed in one borehole may be absent in the next, even at a distance of only 20–50 m, or may shift vertically either upward or downward [23].

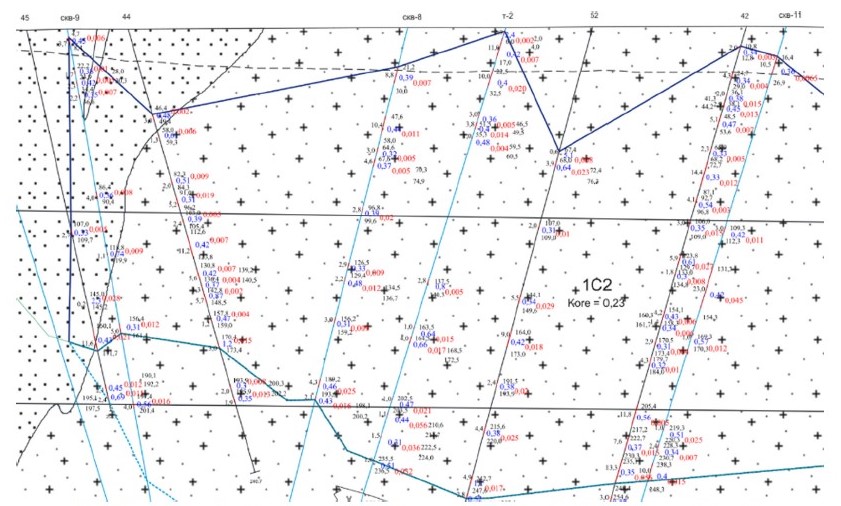
Fig. 2. Geological and resource estimation cross-section of the Kaskyrkazgan deposit

1.4. The Naiman-Zhal ore field formed during the Cambrian–Ordovician in an island-arc system developed on oceanic crust. The host rocks are represented by a basalt–terrigenous–siliceous formation corresponding to the initial stage of volcanic activity in the region. This formation is genetically associated with volcanogenic massive sulfide (VMS) polymetallic deposits containing gold and silver, most prominently expressed in the Maikain ore field, which serves as a reference example of this deposit type.

The geological structure of the Naiman-Zhal deposit, covering an area of 2.0 × 0.8 km, is dominated by volcanic and volcanogenic–sedimentary (volcaniclastic) rocks of the Lower and Middle Ordovician. Terrigenous and chemical sediments play a subordinate role, while subvolcanic and intrusive complexes are distinctly minor in the stratigraphic section.

Within the Naiman-Zhal deposit, mineralized zones are distinguished, within which the ore bodies themselves are localized. These zones can be identified in surface workings and boreholes by their characteristic material composition and specific structural–textural features. However, delineating economically significant ore bodies with established cut-off grades for gold (e.g., 0.5 g/t) requires detailed sampling (Fig. 3). The central parts of the ore bodies, enriched in gold and silver, are clearly recognizable by visual features, both in oxidized and semi-oxidized ores as well as in primary gold-bearing ores [24].

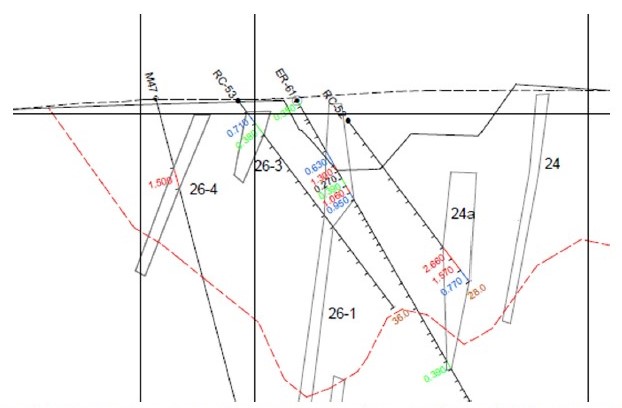
Fig. 3. Geological and resource estimation cross-section along profile 2+25 of the Naiman-Zhal deposit

All of the examined deposits are characterized by complex structural organization. Bench blocks represent intricate combinations of ore bodies and host rocks (subeconomic ore) that differ in:

• configuration;
• size range;
• physical–technical properties;
• geological characteristics.

A distinctive feature of these deposits is the absence of visually discernible boundaries between economic and subeconomic ore, which makes their boundaries probabilistic in nature. A significant drawback is the lack of real-time information on the distribution of valuable components within different parts of a mined block. However, this problem can be addressed through integrated analysis of exploration borehole data. Applying regression analysis methods makes it possible to establish patterns in the variation of ore grades in the boundary zones of subeconomic ore, thereby significantly improving the effectiveness of exploration work.

For a more detailed investigation of valuable component distribution, the following approaches are recommended:

• statistical analysis of sampling data;
• development of regression models for metal distribution;
• assessment of spatial grade variability;
• identification of patterns in ore quality variation within boundary zones.

These studies can substantially enhance the reliability of predictive estimates and support optimization of the mining process.

2. Analytical determination of ore grades in the boundary zones of subeconomic ore

This analysis is based on data from geological boreholes (Fig. 4). Exploration borehole results from the Koktas-Sharykty, Kaskyrkazgan, and Yuzhny-Mointy deposits are summarized in Table 1. These data make it possible to identify patterns of grade variation within the subeconomic portion of a bench block and to more accurately establish trend lines for valuable component distribution beyond the boundaries of economic ore.

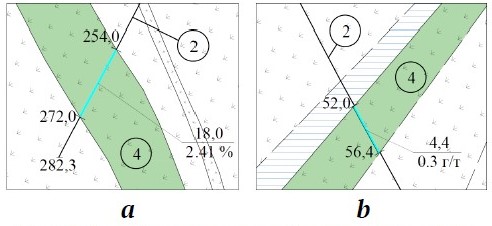
Fig. 4. Schematic representation of exploration boreholes and ore zones at the deposits:
a – Koktas-Sharykty; b – Yuzhny-Mointy; 2 – exploration borehole; 4 – ore body

Table 1

Exploration borehole data from the Koktas-Sharykty (a), Kaskyrkazgan (b), and Yuzhny-Mointy (c) deposits

The procedure for constructing a trend line and determining its equation involves several steps. First, select two consecutive points within the ore body with known ore grades and one point in the adjacent subeconomic ore zone with an established grade (see Fig. 4). Distances between these points are measured from core samples obtained in exploration or production boreholes. The coordinate system is then aligned so that its origin coincides with the first point of the trend line inside the ore body (Fig. 5, a, b). The selected points are connected by a smooth curve. The first segment of the curve (up to the economic ore boundary) reflects ore grade variation within the economic ore, while the second segment describes ore grade variation in the subeconomic portion of the block. The resulting trend line is expressed by the exponential equation:

y′ = A ·e^kx′, (1)

where y′ is the ore grade at a given interval, A and k are coefficients to be determined, and x′ is the distance from the first borehole point to the interval under consideration, m.

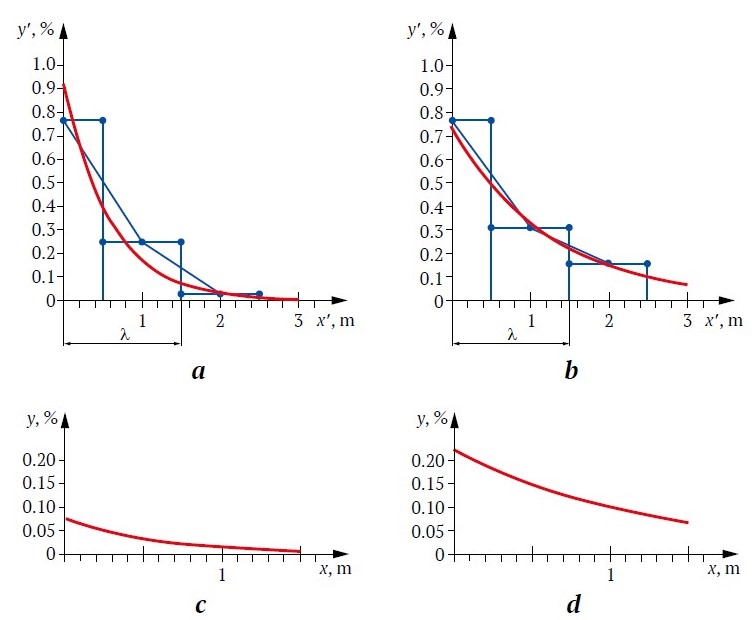
Fig. 5. General trend lines of ore grades in the boundary zones of economic and subeconomic ore based on exploration borehole KAS 2013 72–76 at the Kaskyrkazgan deposit:
a – right boundary of the ore body; b – left boundary of the ore body; trend lines in the subeconomic zone: c – right flank; d – left flank

To determine the coefficients A and k, equation (1) is linearized by applying natural logarithms:

ln y′ = ln A + kx′, Y′ = C + kx′, (2)

where ln y′ = Y′, ln A = C represent the intercept terms of the linear equation.

The values of C and k are obtained using linear regression, which minimizes the sum of squared deviations between observed and estimated values:

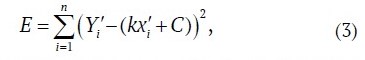
where E is the sum of squared deviations, n is the number of data points, and  is the abscissa of the i-th point.

The coefficients k and C are then calculated as:

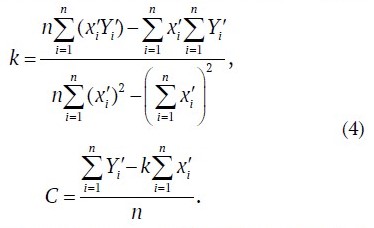
Once k and C are determined, coefficient A can be derived, completing the exponential dependence.

To determine the ore grade (y) in the subeconomic portion of the block, it is necessary to use the segment of the overall trend line corresponding to this zone. To isolate this segment, the origin of a new coordinate system must be aligned with the boundary of the ore body (Fig. 5, c, d), then:

y = A ∙ e^k(x + λ) = A ∙ e^kλ ∙ e^kx, y = A′ ∙ e^kx, (5)

where λ is the distance from the origin of the initial coordinate system to the ore body boundary, and A′ = e^kλ is the trend line coefficient in the subeconomic zone (Fig. 6).

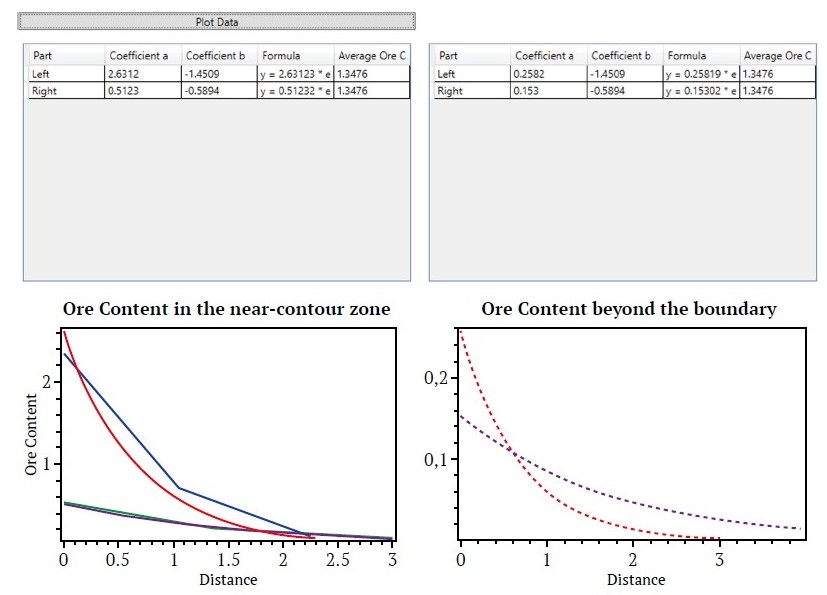
Fig. 6. Program interface for calculating ore grade equations in the boundary zone of subeconomic ore (Coefficient a = A′)

Equation (5) can thus be used to compute ore grades (y) within the subeconomic ore zone. For automated calculations, a program was developed to plot the dependence of ore grade on distance within the boundary zone and determine the coefficients of the exponential equation. The program was written in C# using the Visual Studio 2022 environment (see Fig. 6). To use the program, a *.csv file containing borehole or production drill data for the area of interest (see Table 1) must be uploaded. By pressing the “Plot Data” button, the regression analysis is executed as described above. As shown in Fig. 6, two tables are produced with the trend curve coefficients for the left and right boundaries, presented both in the primary coordinate system (left) and in the transformed coordinate system (right). The graphs below display the grade variation curves for the left and right ore body boundaries in both coordinate systems.

3. Technological justification for complete ore recovery from complex-structured blocks with inclusion of a subeconomic ore layer

Achieving complete ore recovery from complex-structured blocks with minimal losses and dilution requires consideration of several key beneficiation indicators:

• concentrate grade (β);
• tailings grade (δ);
• average ore grade in the feed (α);
• concentrate yield (γ_c);
• tailings yield (γ_t);
• recovery to concentrate (ε_c);
• recovery to tailings (ε_t).

These indicators are usually determined experimentally in laboratory and pilot-scale tests [25–27]. For theoretical calculations, however, mathematical relationships derived in our previous studies [25] can be applied:

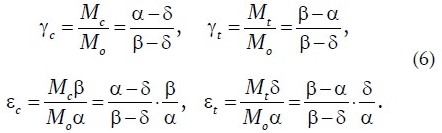Since the masses of the feed ore (M_o), concentrate (M_c), and tailings (M_t) can be measured with high accuracy, the recoveries and beneficiation product yields can likewise be calculated precisely using the formulas given in (6).

The relationship between valuable component recovery and product yields is expressed by the following equations:

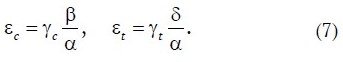Principles of delineating economic ore

When tackling this problem, particular attention should be paid to the methodology for delineating the boundaries of economic ore. This procedure is based on determining the minimum cut-off grade of the valuable component in ore (α) that is both technologically and economically justified. Ore volumes with ore grades below this threshold (< α) are classified as subeconomic and regarded as part of the host rock.

Research has shown that ore grades decrease gradually with distance from the ore body boundary. In the boundary zone of subeconomic ore directly adjacent to the economic ore, the grade corresponds to the cut-off value [12]. With increasing distance from this boundary, the average ore grade of the total mined ore mass (α′) declines.

To quantify this process in two-dimensional representation (Fig. 7), the following equation is applied:

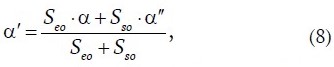where S_eo is the area of economic ore, m²; S_so is the area of the admixed subeconomic ore layer, m², and α′′ is the ore grade in the admixed subeconomic ore.

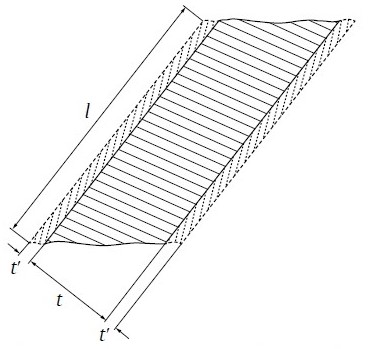
Fig. 7. Schematic for determining ore grade in the shipped ore:
 – economic ore;   – subeconomic ore

These mathematical relationships make it possible to:

• delineate economic ore bodies more precisely;
• calculate optimal mining parameters;
• design algorithms that minimize ore losses;
• reduce ore dilution;
• substantiate the economic feasibility of extracting boundary zones.

This methodology is especially relevant for complex-structured deposits with indistinct ore body boundaries, where conventional delineation approaches often prove inadequate.

To calculate the grade α′′ = y in the admixed layer of subeconomic ore, equation (5) is applied, giving:

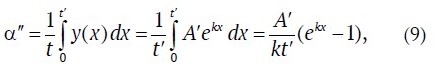
where t′ is the thickness of the admixed subeconomic ore layer. The calculated values of α′′ are presented in Tables 2 and 3.

Table 2

Data for the Kaskyrkazgan copper deposit (a) and the Koktas-Sharykty area (b)

Table 3

Table 3. Data for the Yuzhny-Mointy gold-bearing area (a) and the Naimanjal deposit (b)

To determine the ore grade in the shipped ore, the following algorithm is applied:

1. Define the complex-structured bench block under investigation.
2. Compile ore grade data for the boundary zones of economic and subeconomic ore based on samples from exploration or production boreholes.
3. Input the boundary zone grade data into the developed software, which calculates the coefficients A′, k for the exponential dependence (5) describing grade variation in subeconomic ore.
4. Using the calculated coefficients, determine the ore grade in the admixed subeconomic ore layer according to dependence (9).
5. Substitute the calculated α′′ value into equation (8) to obtain the ore grade of the total shipped ore.

For practical verification of the proposed algorithm, three scenarios of integrated ore extraction were examined in detail. Each scenario involved combined mining of economic ore with adjoining layers of subeconomic mineralization within complex-structured blocks. The ore bodies considered varied substantially in thickness, from 4 to 30 m, which allowed assessment of the algorithm’s performance under diverse geological conditions.

Study parameters for copper ores:

Scenario 1: admixed subeconomic ore layer thickness (t')= 0.3 m; the ore grade in the admixed layer (α′′) varied within the range 0.008–0.02.

Scenario 2: t' = 0.7 m; α′′ = 0.034–0.101.

Scenario 3: t' = 1.0 m; α′′ = 0.059–0.197.

Study parameters for gold-bearing ores:

Scenario 1: t' = 0.3 m; α′′ = 0.008–0.028.

Scenario 2: t' = 0.7 m; α′′ = 0.033–0.13.

Scenario 3: t' = 1.0 m; α′′ = 0.054–0.236.

Ore quality and beneficiation product characteristics:

Feed ore grades: copper ores a_Cu = 0.3–1.0 %; gold-bearing ores a_Au = 0.00005–0.0002 % (0.5–2.0 g/t).

Concentrate grades: copper concentrate b_Cu = 20.0%; gold-bearing concentrate b_Au = 0.04 % (40.0 g/t).

Tailings grades: copper ores d_Cu = 0.06%; gold-bearing ores d_Au = 0.00001 % (0.1 g/t).

Experimental results

The calculated ore grades in the shipped ore and their recoveries to concentrates for copper and gold-bearing ores are summarized in Tables 4 and 5, respectively. Relative deviations of these indicators are analyzed in Tables 6 and 7, providing an assessment of the algorithm’s stability under different initial conditions.

Table 4

Ore grades in shipped ore and their recovery to concentrate at different thicknesses of admixed subeconomic ore layers in the Kaskyrkazgan deposit (a) and the Koktas-Sharykty area (b)

Table 5

Ore grades in shipped ore and their recovery to concentrate at different thicknesses of admixed subeconomic ore layers in the Yuzhny-Mointy area (a) and the Naimanjal deposit (b)

Table 6

Relative deviations of the studied indicators from the required values at different thicknesses of admixed subeconomic ore layers in the Kaskyrkazgan deposit (a) and the Koktas-Sharykty area (b)

Table 7

Relative deviations of the studied indicators from the required values at different thicknesses of admixed subeconomic ore layers in the Yuzhny-Mointy area (a) and the Naimanjal deposit (b)

The findings demonstrate the effectiveness of the proposed approach to mining complex-structured ore blocks, ensuring:

• higher recovery of valuable minerals;
• controlled incorporation of subeconomic ore into production;
• opportunities for optimizing process parameters;
• reduction of valuable component losses;
• reduced dilution of the mined ore mass.

The validation results confirm the versatility of the developed algorithm across different ore types and a wide range of geological conditions.

As shown by the data in Tables 4 and 5, there is a clear dependence of the ore grade in the shipped ore mass on two key factors. First, there is a direct correlation between the ore grade in economic ore and its concentration in the shipped material. Second, an inverse relationship is observed with respect to the distance from the ore body boundary: as the distance from the boundary of economic mineralization increases, the ore grade consistently decreases. This relationship is equally characteristic of both copper and gold-bearing ores, and it is evident in all the extraction scenarios considered. It is noteworthy that a similar trend, though somewhat less pronounced, is also observed in the recovery of copper and gold to concentrate. In this case, however, the amplitude of variations is much smaller, indicating the relatively stable nature of the beneficiation process.

For a more detailed assessment of how these changes affect the final technological outcome – namely, the recovery of the valuable component to concentrate – a comparative analysis of deviations across all three scenarios is required. Such an approach makes it possible to:

• determine the sensitivity of the technological process to variations in the initial ore grade;
• assess the influence of distance from the ore body boundary on beneficiation efficiency;
• define mining parameters for each ore type;
• evaluate the stability of processing equipment performance under changing conditions;

develop corrective measures to minimize the negative effects of the identified factors.

According to the data presented in Tables 6 and 7, clear patterns can be observed in the variation of ore grades in shipped ore.

For copper ores, the maximum relative deviation does not exceed 6% in Scenario I, increases to 16% in Scenario II, and reaches 22% in Scenario III.

For gold-bearing ores, the maximum deviation is 10% in Scenario I, rises to 24% in Scenario II, and reaches 31% in Scenario III.

Analysis of valuable component recovery to concentrate reveals a clear trend.

For copper ores, deviations range from 0.3 to 0.97% in Scenario I, from 0.72 to 2.38% in Scenario II, and from 1.05 to 3.55% in Scenario III.

For gold-bearing ores, deviations range from 0.13 to 1.52% in Scenario I, from 0.34 to 4.52% in Scenario II, and from 0.49 to 6.57% in Scenario III.

All observed deviations in recovery remain within technologically acceptable limits, confirming the effectiveness of the proposed method.

The application of new technological solutions for recovering economic ore from complex-structured blocks with partial inclusion of subeconomic ore makes it possible to:

• ensure the required quality of shipped ore mass;
• significantly increase the volume of extracted raw material;
• enhance the overall efficiency of deposit exploitation.

The implementation of this new technology for mining complex-structured blocks results in the following:

• a portion of subeconomic ore previously considered as diluting waste is reclassified as recoverable reserves;
• the volume of extracted ore mass increases substantially;
• the percentage recovery of valuable components to the final concentrate improves.

4. Economic impact

Under actual production conditions at a copper open-pit mine with an annual ore output of 6–7 Mt, an average copper grade of 0.45%, and complex-structured blocks accounting for 50–60% of the total, the additional recovery of valuable components may reach 10–15% of overall production.

Thus, the proposed technology delivers a significant technological and economic impact while maintaining the required quality of the mined ore mass.

Conclusion

1. Based on analysis of exploration borehole data from five copper and gold-bearing ore deposits in Kazakhstan (Kaskyrkazgan, Koktas-Sharykty, Yuzhny-Mointy, Naiman-Zhal, and others), regularities in the variation of ore grades in the boundary zones of subeconomic ore have been established. It was determined that these grades follow an exponential relationship of the formy = А′∙e^kx, with parameters varying as follows: for copper ores, А′ = 0.10–23, k= −0.32–−1.94; for gold-bearing ores, А′ = 0.10–0.36, k= −0.45–−2.19.
2. An automated software tool was developed in C# within the Visual Studio 2022 environment to calculate exponential trend equations, determine coefficients A′ and k, and forecast ore grades in the admixed subeconomic ore layer.
3. Using this software, calculations were performed to determine grades in the shipped ore (α′) when admixing subeconomic ore layers of varying thickness (t′ = 0.3, 0.7, and 1.0 m). It was shown that for copper ores, α′ varied from 0.406 to 0.270%, with recovery to concentrate ε_c decreasing from 94.10 to 78.03 %; for gold-bearing ores, α′ varied from 0.931 to 0.248 г/т, with recovery to concentrate ε_c decreasing from 94.28 to76.02 %.
4. In the first case of admixing a 0.3 m subeconomic ore layer, relative deviations in ore grade of shipped ore were 2.14–6.91% for copper ores and 1.49–9.39% for gold-bearing ores. The corresponding deviations in recovery to concentrate were 0.3–0.97% for copper and 0.13–1.52% for gold, all within acceptable technological limits.
5. The proposed approach for complete recovery of economic ore through controlled admixing of boundary subeconomic material ensures the required quality of shipped ore while increasing extractable reserves. This has been confirmed by calculations for admixed layers of varying thickness.
6. For the first time in mining science, the theoretical feasibility of reclassifying part of the diluting subeconomic ore into recoverable reserves has been substantiated. This leads to an increase in shipped ore tonnage and recovery of valuable components to concentrate without compromising concentrate quality.

The results obtained are of considerable practical significance. In the case of an open-pit mine with an annual ore production of 6–7 Mt, an average copper grade of 0.45%, and complex-structured blocks accounting for 50–60% of total production, additional copper recovery may reach 10–15% of overall output. In monetary terms, this corresponds to an additional annual profit of approximately USD 15.3 million, assuming a market copper price of USD 8,500 per ton.