Comprehensive study of the anisotropy of microstructural and filtration properties of a gas condensate field reservoir based on digital core analysis

Introduction

Modern technologies based on numerical simulation and X-ray microtomography provide new opportunities for detailed study of a reservoir pore space and prediction of its filtration properties [1, 2]. However, traditional assessment methods (laboratory measurements using a core [3], hydrodynamic well studies, empirical correlations [4]) do not take into account the microstructure of the pore framework and often do not allow reliable prediction of permeability based solely on porosity [4]. This is particularly relevant for poorly consolidated sandstones in gas condensate offshore fields, where reservoir stability and filtration efficiency [5] often depend not only on pore volume, but also on their spatial arrangement [6]. The use of digital core twins based on microtomographic data allows reproducing the topology of the pore space [7, 8] and improving the reliability of productivity forecasts [9].

One of the key tasks of digital analysis is the quantitative characterization of parameters affecting filtration processes, including open and closed porosity [7, 9], tortuosity [10], percolation channel structure [11], and directional (anisotropic) variability of these parameters [12, 13]. This is particularly important when exploiting formations (reservoirs) with horizontal wells, where drainage efficiency can significantly depend on the orientation of the wellbore relative to the textural features of the reservoir [14, 15].

The number and morphology of filtration channels are critical in the development of offshore fields [16], where operational errors can lead to sand production, rock removal, and a sharp drop in permeability [17, 18]. In poorly consolidated rocks, the stability of well walls [19] and local permeability are determined not so much by averaged characteristics [20] as by microstructural parameters of the pore framework, including substructural anisotropy [21, 22]. Despite the increasing importance of considering the above characteristics, most studies are limited to isotropic models or focus on porosity, without taking into account the complex influence of pore morphology on filtration [23, 24].

The aim of this study is to quantitatively describe the anisotropy of filtration properties, a targeted analysis of morphometric characteristics and their relationship to permeability for poorly consolidated sandstones in a pay interval of a gas condensate field on the northern shelf based on digital core twins, followed by interpretation of the results for hydrodynamic simulation, the propagation of the filtration front in a formation, and designing horizontal well directions. The scientific novelty of the work lies in performing a comprehensive digital assessment of the spatial anisotropy of a pore space, taking into account the morphological and physical characteristics of a reservoir, establishing the fact of stable substructural anisotropy within the bedding plane for the field under consideration, justifying the directions for drilling horizontal wells in conditions of textural heterogeneity of the formation, conclusions about the risks of local pressure accumulation in the formation and capillary isolation of condensate.

To achieve this goal, the following tasks were set:

1. Building digital twins of the core based on high-resolution microtomographic data.
2. Determination of open and closed porosity, tortuosity, percolation path parameters, and assessment of their directional variation.
3. Numerical simulation of filtration flow in three orthogonal directions with permeability calculation.
4. Analysis of the relationship between the geometric characteristics of the pore space and filtration properties.
5. Determination of representative elementary volume (REV) and justification of the reliability of the digital model.

1. Research Technique and Subjects

The subject of the study was the reservoir rocks of a pay intervals of a gas condensate field located on the northern shelf of Russia. The rocks are represented by poorly consolidated sandstones characterized by low strength and high porosity and permeability. This extracted reservoir is characterized by the lack of pronounced visual bedding and is subject to intense sanding. Core fragments were selected from the pay interval, followed by the preparation of more than 10 samples of arbitrary shape with dimensions ranging from 5 to 20 mm. X-ray computed microtomography method was used to study the pore space. The scanning was performed using Procon X-Ray CT-MINI instrument from the Institute of Mechanics Problems of the Russian Academy of Sciences [9]. The obtained tomographic data consisted of sets of slices with a resolution (voxel = cubic pixel size [25]) of 4.995 μm, reconstructed into three-dimensional digital models of core fragments. All samples had a similar structural composition that confirms the representativeness of the sample set, but for subsequent digital analysis, samples with a complete absence of fracturing were selected, which may be the result of the influence of transportation and storage conditions on the fracturing-prone material.

After reconstruction and processing (including Gradient and/or Gaussian Brightness correction [26], filtering with Non-local Means algorithms [27]), segmentation [28] of tomographic images was performed to distinguish two phases: pore space (air) and solid matrix (grains). VGStudio software [29] was used for the reconstruction, as well as proprietary algorithms for processing 3D images. Threshold algorithms based on the analysis of the intensity distribution histogram were used for the segmentation [28]. As a result, a binary voxel model (a digital twin) was formed, in which each voxel was designated as either porous or matrix. Such models serve as the basis for subsequent calculations. Figure 1 shows the main stages of processing and segmentation of the tomographic data.

Fig. 1. The main stages of preprocessing and segmentation of tomographic data:
a – part of the projection of the reconstructed image; b – part of the projection of the image after preliminary processing and smoothing; c – the same area after segmentation into two phases: gray represents matrix grains, white represents pores

Digital analysis of the pore space included:

• assessment of open and closed porosity in three orthogonal directions;
• calculation of geodesic tortuosity (minimum, maximum, and average) based on algorithms for finding the shortest paths from one face of a three-dimensional binary model to the opposite face;
• identification and analysis of percolation paths including calculation of their length and diameter of constrictions (maximum diameter of a particle passing through a channel);
• numerical simulation of filtration flow based on the Navier–Stokes model using laminar flow conditions to estimate permeability and flow distribution in each direction;
• construction of visual maps of velocities, pressure gradients, and porosity distribution by layers for qualitative interpretation of the spatial structure of the pore framework.

The pore space analysis was performed in GeoDict [30]. Open and closed porosity was calculated by counting the proportions of pore voxels. Open porosity was defined as the proportion of voxels that are connected to one of the outer faces of the model and form a through path. Closed porosity refers to isolated pores that are not connected to external faces. These values were calculated separately for three orthogonal directions.

Geodesic tortuosity was assessed based on the construction of the shortest paths from one face of a sample to the opposite face in each direction. Tortuosity was determined as the ratio of the path length through the pore space to the geometric length of the sample.

Unlike tortuosity, which can take into account narrow areas inaccessible to real fluid, the percolation path search algorithm constructed physically realistic trajectories, taking into account the diameter of a passing particle. The algorithm excluded paths with bottlenecks (throats) smaller than the specified diameter and selected those channels through which a particle could pass without disrupting continuity. For each direction, the following were calculated: the length of the percolation path (the actual distance that a particle would travel); the maximum diameter (the minimum cross-sectional size along the path, the narrowest point) determining passability. As a result of visualization, a set of filtration channels corresponding to the physical conditions of fluid conductivity was obtained. Thus, the study applied a physically oriented approach to percolation, allowing the identification of effective filtration flow trajectories, taking into account geometric constraints.

Based on the binary model, fluid (air) flow through a pore space was simulated using the Navier–Stokes equations [31] in a steady laminar configuration:

−μΔū + ρ(ū ⋅∇)ū +∇p = ḟ  ,

where μ is fluid viscosity, Pa·s; ū is fluid velocity, m/s; ρ is fluid density, kg/m³; p is pressure, Pa;  ḟ is body force, N/m³.

The mass conservation equation in this case takes the form:

∇⋅ū = 0.

The permeability of a material can be calculated using Darcy's law:

Q = −kA/μ · (P_b − P_a)/L,

where Q is fluid flow rate, m³/s; k is permeability of the medium, m²; A is cross-sectional area of the flow, m²; μ is viscosity of the fluid, Pa·s; P_b and P_a are pressures, Pa; L is the length over which this pressure drop occurs, m.

In this study, the LIR solver [32] was used for numerical simulation of filtration. The calculations were performed with a specified pressure drop of 100 Pa. The criterion for completing the calculations is an error bound of 0.1 [33]. Periodic boundary conditions with 10-voxel layers at the inlet and outlet were set in the calculation direction to ensure flow uniformity. Symmetric boundary conditions were set in the tangential direction [33]. The following were calculated at the output: velocity and pressure fields; integral permeability value for each direction (according to Darcy's generalized law); visualization of velocity channels reflecting active filtration paths. Unlike traditional permeability assessment methods, such as laboratory filtration tests, φ–k correlations, and Carman-Kozeny models, the approach used is based on direct numerical simulation of filtration using 3D microtomography data. It allows not only to take into account the actual geometry of the pore space and anisotropy, but also to conduct a detailed analysis of the structure of filtration channels.

To accurately assess the heterogeneity of the pore space structure, layer-by-layer porosity cartograms were constructed [34]. The model was averaged across layers perpendicular to the selected axis, and then the porosity was displayed as a two-dimensional color map. This made it possible to identify vertical or horizontal fluctuations in the structure and visually assess the homogeneity of a sample.

In addition to numerical simulation, laboratory measurements of permeability along Z axis of core and in XY bedding plane were carried out at the TILTS installation of IPMech RAS installation [9]. The laboratory values obtained were used to validate the digital model and compare it with the results of direct numerical calculations.

2. The findings and discussion

Table 1 shows the summary results of the digital analysis for three characteristic samples. The final digital samples were cubes measuring 500 voxels, which were used to perform filtration calculations in three mutually perpendicular directions, X, Y, and Z (Z axis coincided with the longitudinal axis of a core). The table includes the values of geodesic tortuosity (minimum, maximum, and average), length calculated during the assessment of trajectory tortuosity (minimum, maximum, and average), percolation path parameters (average maximum particle diameter and average physical path length across all channels in a given direction), as well as open and closed porosity values and calculated permeability. The table is structured by sample: rows are grouped by sample number, each row corresponds to one simulation direction.

Table 1

Summary results of the digital analysis

The obtained porosity data demonstrate high uniformity of the pore space both in quantitative terms and in spatial distribution. The open porosity in all three orthogonal directions is practically identical and amounts to about 26% (see Table 1), with differences between the directions not exceeding hundredths of a percent. The maximum open porosity value is observed along X-axis (≈ 26.007%), the minimum one is along Y-axis (≈ 25.995%), and along Z-axis the value is ≈ 26.008%. Thus, the difference in open porosity between X, Y, and Z is negligible (no more than 0.013 percentage points) that indicates the absence of directional anisotropy of open porosity and confirms the textural homogeneity of the samples. The standard deviation of the open porosity values between the samples for each direction does not exceed 0.005%, and the coefficient of variation is less than 0.02% that indicates high reproducibility of the results obtained. Closed porosity also demonstrates very low values (in the order of tenths of a percent) and varies insignificantly between directions. It is unusual that in Y direction it turned out to be slightly higher (≈0.413%) compared to Z (≈0.204%) and X (≈0.176%). At first glance, this result contradicts the expected effect: normally, a higher proportion of isolated pores (closed porosity) should impair filtration properties. In this case, however, the difference is so small in absolute terms that its effect is not noticeable — Y direction remains the most permeable even with increased closed porosity. Low Dead-end porosity values confirm the high degree of connectivity of the void space and correlate with the proportion of closed pores that may indicate their occurrence mainly due to the intersection of isolated pores by the boundaries of the structures under consideration.  On the whole, such a small variation in porosity values (less than 0.5 % relative) allows the pore framework to be considered practically isotropic in terms of porosity.

The geodesic tortuosity of the pore space shows limited, albeit stable, fluctuations from ~1.03 to 1.26. These values indicate that the actual filtration paths are only slightly longer than the direct (geometric) size of a sample. The variation in average tortuosity between different samples is insignificant (at standard deviation of ~0.01, coefficient of variation of ~1%) that emphasizes the reproducibility of this parameter. An atypical difference is observed in the bedding plane ( X and Y axes): the average tortuosity  along Y axis is slightly less than that along X axis (by ~3–4%), despite the location of both directions in the rock bedding plane. At the same time, Z axis (core axis) predictably shows higher tortuosity reflecting the influence of bedding. Nevertheless, all τ values obtained remain low (~1.1), confirming the high connectivity of the pore channels.

Analysis of percolation paths provided additional information about the geometry of the pore space that goes beyond purely geodesic characteristics. For each direction (X, Y, Z), 100 percolation paths were determined, representing physically realizable trajectories along which a particle could pass through the pore system. Unlike tortuosity, which reflects only the length of a geometric curve, the percolation algorithm takes into account the minimum sizes of pore bottlenecks capable of passing a particle of a certain diameter. Fig. 2 shows, using one of the samples as an example, the percolation paths in three orthogonal directions (a – X, b – Y, c – Z) with a color gradient superimposed, representing the length of each trajectory from the input to the output surface. In all three directions, the percolation channels form an organized, well-connected network structure with long continuous flow zones, without sharp local distortions or spots that could indicate the presence of areas requiring bypassing or indicating local barriers.

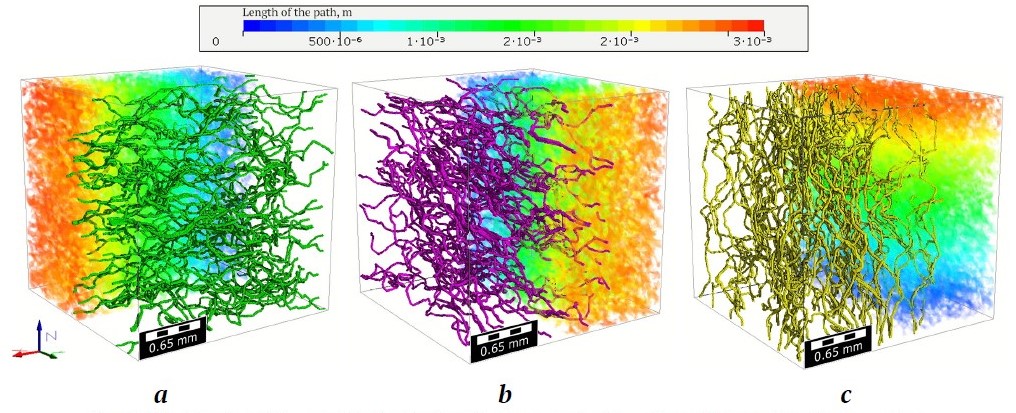
Fig. 2. Visualization of the spatial distribution of some percolation paths and integral gradient mapping of path lengths along X, Y, and Z axes

Fig. 3 shows the distribution of filtration flow velocities; in all cases, similar elongated areas of high velocities corresponding to the "main" flow channels are visible. This indicates that the samples contain directed filtration pathways with minimal geometric obstacles and confirms that the degree of connectivity of the pore space is high in any direction. Thus, despite the weak anisotropy of filtration properties (see below), the geometry of the pore framework itself is close to isotropic, in terms of both integral indicators (porosity, tortuosity) and the structural arrangement of percolation paths.

Fig. 3. Visualization of spatial distribution of filtration flow velocities along X, Y, and Z axes

Unlike porosity, filtration properties exhibit weak but distinct anisotropy. The calculated permeability values (see Table 1) differ between the three axes. A weak manifestation of an atypical type of anisotropy is observed: one of the horizontal directions X turned out to be less permeable than the vertical direction Z, and the preferred filtration flow is oriented along Y axis. Quantitatively, this anisotropy is small (ratios  k_Y : k_X ≈ 1.3, k_Y : k_Z ≈ 1.2), but it is consistently reproduced in all samples. The spread of permeability values between different samples for each axis does not exceed 0.01 D (relative coefficient of variation < 0.5%), thanks to which the difference identified between X, Y, and Z is statistically significant and is due to the microstructure of the rock. This is confirmed by independent physical tests: the laboratory measurements on core material showed permeability of ~5.6 D along the core axis and ~6.1 D in the XY bedding plane. Although the absolute values in the laboratory proved slightly higher, the ratio between the directions is similar to the model data, indicating the presence of weak but stable transverse anisotropy of the filtration properties of the rock. The good agreement between the numerical simulation and the tests results confirms the correctness of the digital approach used and the adequacy of the model for simulating the actual filtration behavior of the samples.

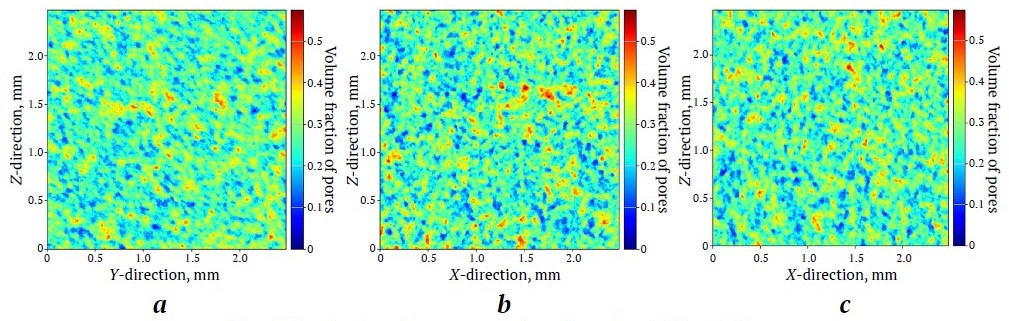
Fig. 4. Distribution of average porosity values along X, Y, and Z axes

Porosity cartograms obtained by layer-by-layer averaging in each direction are shown in Fig. 4. The color scale reflects local porosity values, where blue corresponds to minimum values, red to maximum values. In all three projections (a –  YZ, b –  XZ, c –  XY), the distribution of the values demonstrates a similar structure: the images are dominated by areas with a uniform transition from blue to green-yellow shades, which corresponds to porosity values close to the average value. Local deviations occur, but do not form clusters or pronounced directional anomalies. This indicates that the structure of the pore space retains a near-isotropic character not only in terms of integral values, but also in terms of pore distribution in volume. This suggests that the observed differences in filtration properties are not related to porosity as such, but to the geometry of the pore connections — their tortuosity, throat width, and degree of connectivity.

The results show that, with the same porosity, differences in pore space geometry (tortuosity, channel size, connectivity) significantly affect permeability. Y direction demonstrates the highest permeability, combining minimal average tortuosity and a slightly larger average pore channel diameter (see Table 1). According to the Carman-Kozeny equation (as modified by Becker) for a homogeneous porous medium:

k = φ³/(1 − φ)² · 1/(Cτ²S₀²),

where φ is porosity; C is a structure constant; τ is tortuosity coefficient; S₀ is specific surface area of grains. The ratio is a qualitative illustration of known relationships, but is often used for a preliminary assessment of the properties of porous media. The porosity in the samples under consideration is almost constant (φ ≈ 26%), and differences in specific surface area can be estimated based on the characteristic size of the pore channel. Assuming that S₀ is inversely proportional to average pore diameter d, the formula can be simplified to: k ∝ d²/τ². This reflects the intuitively expected relationship: an increase in the cross-sectional area of a flow (larger d) and a decrease in tortuosity (smaller τ) increase permeability. Indeed, the observed anisotropy is consistent with this model: Y direction has the largest average pore diameter (~22.8 μm) and the lowest tortuosity (~1.08), thus demonstrating the maximum k.

However, quantitatively, the classical model underestimates the effect. Calculations show that with a decrease in τ of only ~3% and an increase in d of ~1% (in Y direction relative to X), the relative increase in k should be only about 10%, whereas according to the simulation, it reaches ~30%. Similarly, the Katz–Thompson percolation model (which links permeability to the square of the critical pore channel radius) predicts nearly equal values of k for X and Y due to the virtually identical size of the "bottlenecks" (in the case under consideration, the average maximum diameter of the limiting holes differs by less than 1%). Thus, the standard models do not fully explain the observed anisotropy that indicates the presence of additional factors. The higher permeability along Y-axis is probably due to the fine-scale arrangement of the pore channels, which is not directly reflected in the averaged parameters d and τ (e.g., pore network configuration, radius distribution, etc.). In Y direction, more direct and through flows are realized due to the lithological orderliness of the structure, while in X direction, some of the channels are blocked or deflected. In other words, the permeability of poorly consolidated sandstones is extremely sensitive to the changes in the tortuosity and connectivity of pores: even a slight "straightening" of the channels results in a disproportionately large increase in k. Similar conclusions are made in [35], which shows that in sandstone and carbonate, the logarithmic relationship between permeability and porosity has a large spread and strongly depends on sorting and diagenesis. This observation is confirmed in the present study, which highlights the limitations of using porosity alone as a prognostic parameter. Similarly, in a later work [36], based on statistical simulation of 13,000 porous structures, it was concluded that the correlation between permeability and porosity may be insufficient, especially at porosities below 0.7, and that geometric parameters such as tortuosity and conductivity, when correctly formalized, provide a more accurate description of the filtration characteristics of a pore space. A similar relationship between porosity and permeability is emphasized for oil-bearing sandstones in [37]. It is particularly important that, despite its minimal open porosity, Y direction proved to be the most permeable that is consistent with the hypotheses [38] about the role of lithological orderliness and textural orientation in the formation of effective filtration channels. This highlights the need for a comprehensive approach to assessing reservoir properties, including not only classic petrophysical parameters, but also topological analysis of the pore network, direct hydrodynamic simulation, and morphological characterization of the pore framework.

To correctly evaluate the parameters of the pore space of a digital model, it is necessary to determine the representative elementary volume (REV) – the minimum volume of a porous medium for which the values of the characteristics under study (in this case, porosity) become statistically stable and cease to depend on a sample set size. Knowledge of this parameter ensures the reliability and reproducibility of further calculations, in particular, the simulation of filtration processes and permeability assessment.

To numerically determine REV, a method was used involving the step-by-step division of the digital model into smaller domains, followed by analysis of the porosity distribution in each of them. Within this approach, the three-dimensional binary model (obtained after reconstruction and segmentation) was sequentially divided into cubic domains of various sizes: from large (300 voxels per edge) to smaller (10 voxels per edge). At each stage of the division, the porosity of each selected domain was determined, after which a cumulative curve of porosity values was constructed.

Fig. 5. Visualization of the Process of Determining the Representative Elementary Volume (REV) by the Method of Sequential Reduction of Domain Size

Fig. 5 shows the general process of dividing the initial models into smaller domains. Figure 6 shows the results of quantitative analysis of domain porosity: the horizontal axis shows the linear dimensions of the domains (in voxels), and the vertical axis shows the calculated porosity value for each domain. Each blue dot corresponds to the porosity of a single domain of a given size, and the red dotted line corresponds to the average porosity value for the corresponding scale. A decrease in the spread of values as the domain size increases indicates that the parameter has reached statistical stability. As can be seen from the graph, for large domain sizes (more than 150 voxels), the spread of porosity values between different domains becomes minimal, and the average value stabilizes. When calculations fall below this threshold, the characteristics lose stability that can lead to incorrect generalizations based on the model. All calculations performed in this work were carried out on models with linear dimensions of 500 voxels. An assessment of REV was also carried out based on a sandstone model quality control algorithm, which confirmed the adequacy of the structure size used (N(REV) > 25). This approach takes into account the ratio of the minimum structure length to the effective grain diameter [40] and provides a reliable estimate of REV for single-phase fluid flow in sandstones.

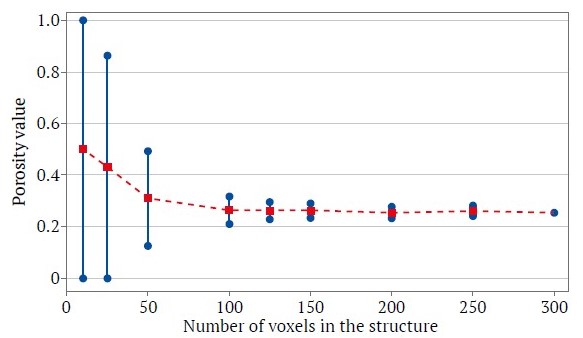
Fig. 6. Dependence of Porosity Value on Domain Size (Number of Voxels per Edge) When Determining Representative Elementary Volume (REV)

3. Practical Conclusions and Recommendations

The identified permeability anisotropy is associated with the oriented structure of the pore space in the bedding plane. The identified profile confirms the feasibility of drilling horizontal wells along a formation — in the direction of the natural rock texture, where the most conductive filtration channels are formed. Special attention should be paid to the choice of well direction in the plane of bedding due to the manifestation of atypical anisotropy: correct orientation of wellbores will allow maximum utilization of highly permeable paths and maximize formation drainage.

The high degree of connectivity of the pore space and the absence of barrier anisotropy in throat opening indicate uniform filtration in all directions. This means that the displacement front (for example, when pumping or advancing a gas/water front) will be stable and uniform, without premature breakthrough in certain directions. The uniform internal architecture is also conducive to complete drainage of a formation and efficient involving condensate into the flow. The minimal proportion of isolated pores (closed porosity < 0.5%) and large pore throats reduce the risk of capillary isolation of condensate – the liquid phase does not get stuck in micropores, but continues to participate in filtration. This ensures more stable exploitation of a gas condensate reservoir without a sharp drop in productivity due to the formation of stagnant condensate zones.

Knowledge of the morphometric characteristics of pore networks allows for more accurate selection of the optimal propant size for hydraulic fracturing and the degree of filtration of the injected water. This prevents pore blockage by particles and the removal of rock material that preserves the permeability of a formation. The digital analysis methods used allow for reliable assessment of filtration and storage properties in conditions of limited core material and can provide rapid assessment of a reservoir at the exploration stage: prompt receipt of data on porosity, permeability, and anisotropy speeds up decision-making, reducing dependence on lengthy laboratory studies.

A detailed analysis of microstructure made it possible to assess the rock's vulnerabilities in terms of particle removal. The visualization of the flows revealed the presence of continuous high-speed filtration channels. In poorly consolidated sandstones, such flow concentration zones can cause increased stress on the matrix and contribute to grain removal. However, the uniform distribution of pores and high total connected pore space mean that there are no pronounced "bottlenecks" where the velocity would increase extremely locally. This reduces the risk of sudden sand production. The results obtained should be taken into account when designing well operating modes: preventing excessive depressions and ensuring uniform distribution of withdrawal across the formation will contribute to the stability of the well walls. Integrating the obtained data into geotechnical models will enable quantitative prediction of critical pressure gradients at which rock failure is possible, thereby minimizing the risk of sand production.

4. Research Prospects

Further development of research areas is planned by substantiating models of pore space tortuosity in poorly consolidated sandstones and identifying its impact on the filtration properties of these rocks. It is planned to clarify the boundary conditions for the applicability of the Carman-Kozeny equation and percolation models for the poorly consolidated reservoirs under consideration. A separate task is to ensure the scalability of parameters from the micro level to core and formation scales so that digital models better reflect the properties at a formation level. An important area of focus is the development of digital models of pore space for the use in simulation of multiphase or thermo-hydromechanical processes that will allow for the consideration of actual conditions in a reservoir. In addition, the development of machine learning methods for automatic prediction of filtration and capacity properties based on microstructural analysis data is equally relevant.

From an applied perspective, one of the key areas for further research is the development of procedures for rapid assessment of permeability using digital models. An important task is to integrate the results of digital simulation into geological and hydrodynamic models of fields, especially when the amount of source data is limited. The practical significance lies in adapting the methodology to rocks with complex and heterogeneous pore structures (e.g., carbonates and fractured sandstones) that will allow the approach to be extended to a wider class of reservoirs.

Conclusion

A study of the anisotropy of the filtration and storage properties of poorly consolidated sandstones in a gas condensate field based on digital core analysis has provided new data on the relationship between the microstructure of a pore space and filtration characteristics. A comprehensive approach involving microtomography, 3D simulation, and numerical calculations confirmed the high accuracy of digital methods in assessing reservoir properties, especially in conditions of limited core material, and also allowed a number of conclusions to be drawn that are important for assessing reservoir properties and optimizing reservoir development.

1. The open porosity values are practically identical in all directions (~26%), but the permeability shows a weak but stable atypical anisotropy. The highest permeability values are observed along one of the directions in the bedding plane that was associated with reduced tortuosity and pore size in this direction.
2. It has been shown that, with the same porosity, permeability significantly depends on the tortuosity of the channels, the width of the throats, and the connectivity of the pores. Classic Carman-Kozeny models underestimate the influence of these factors that highlights the need for a comprehensive analysis of pore space morphology.
3. The optimal direction of horizontal wells should take into account the identified features of permeability anisotropy (up to 30% difference in different directions) to maximize drainage that will allow maximum utilization of the most permeable paths towards a well, contribute to a reduction in depression at the same withdrawal rates, and help improve formation coverage when injecting working agents.
4. The established uniformity of the pore space structure, including the diameter of the filtered particles, helps minimize the risk of sand production by reducing local filtration flow velocities. In addition, low closed porosity values reduce the likelihood of capillary lock-up of condensate.
5. Digital methods enable rapid assessment of reservoir properties during exploration and minimize uncertainty when core samples are scarce. This requires a minimal sample volume (starting from 5 mm³), which is critically important for offshore fields with a shortage of core material. The wide range of data obtained can be quickly integrated into hydrodynamic models, significantly improving their predictive capabilities. The results of numerical simulation are in good agreement with laboratory measurements, confirming the reliability of the approach for predicting filtration properties in complex geological conditions.

Thus, the work demonstrates the effectiveness of digital technologies for studying reservoir anisotropy and provides tools for optimizing field development, especially in offshore production conditions, where access to physical samples is limited and the requirements for forecast reliability are high. Further research may focus on refining tortuosity models and scaling the results to the scale of a formation.