Scroll to:
Reliability analysis of mine ventilation fans based on Markov process theory
https://doi.org/10.17073/2500-0632-2025-03-401
Abstract
The reliability of mine ventilation fans plays a crucial role in aerological systems and is determined by a combination of various geological, mining-technological, and structural factors, most of which are stochastic in nature. The problem of quantifying the reliability indicators of mine fan installations is addressed using various mathematical methods for modeling random processes. This study considers the possibility of applying Markov process theory to develop a methodology for calculating the operational reliability of centrifugal main mine ventilation fans, using the VShTs-16 as an example. The limitations of applying Markov processes to reliability analysis are demonstrated, particularly due to the condition of stochastic independence of failures. The use of homogeneous Markov processes has its constraints, since the transition intensities between individual system states are not always constant. In such cases, it is impossible to construct a system of differential equations with time-dependent coefficients. When stochastic dependence is present in failure flows of mechanical systems, the application of Markov process theory remains possible, but the most effective tool for reliability analysis in such cases is the Monte Carlo numerical simulation method.
Keywords
For citations:
Vyatkin P.V., Valiev N.G., Simisinov D.I., Volkov E.B. Reliability analysis of mine ventilation fans based on Markov process theory. Mining Science and Technology (Russia). 2025;10(3):289-297. https://doi.org/10.17073/2500-0632-2025-03-401
Reliability analysis of mine ventilation fans based on Markov process theory
Introduction
According to Rostechnadzor, aerological risk factors in underground mining remain at a high level. With enterprises transitioning to underground mining under complex geological and mining-technological conditions, and with increasing mining depths in operating mines, the efficiency requirements for ventilation and degassing systems are becoming more stringent [1–3]. The failure-free operation of mine ventilation fans plays a key role in aerological systems.
The reliability of mine ventilation fans is influenced by a range of geological, mining-technological, and structural factors, most of which are stochastic in nature [4, 5].
Quantitative indicators of reliability are determined using various mathematical methods for modeling random processes. The fundamental concepts and reliability measures of ventilation fans were first introduced through the state function method, the critical path method, the statistical method, and statistical simulation [6, 7], as well as fuzzy logic approaches [8].
The mathematical framework of reliability theory is broad, but mathematical statistics, probability theory, and the theory of random processes hold a central position. The concept of reliability in complex technical systems has led to the extensive use of Markov process theory as a mathematical tool. This approach has been successfully applied in analyzing the operability of complex electronic devices and systems [9, 10]. Reliability theory itself, as a general engineering discipline, was shaped largely by advances in radio electronics, computer technology, and rocket engineering, although reliability issues were first raised in the 1930s by specialists in structural mechanics and power systems. Consequently, the mathematical methods most widely adopted in reliability theory were those that met the requirements of computing technology.
The analysis of mechanical system operability emerged later as a second direction in the development of general reliability theory. The mathematical toolkit of this field was significantly enriched by methods and theories that had been deeply developed and broadly applied in electronics. In some cases, however, such borrowing has been applied without sufficient consideration of the specifics of the systems under study and without adequate analysis of the physics of failures. This is particularly relevant to the use of Markov process theory in analyzing the reliability of mechanical systems. In studies [11–13], the authors employ Markov process theory to develop methodologies for engineering calculations of the reliability indicators of specific mechanical engineering products and their manufacturing processes.
Theory
According to the definition in [14], a Markov process is a random process ξ(t), t ≥ t0, that satisfies the condition
p(s, x, t, B) = P{f(s, x, t) ∈ B}, B ⊆ R1, t ≥ S,
under
ξ(s1) = x1, …, ξ(sm) = xm, ξ(s) = x,
independently of х1, х2, … хm.
This property, known as the Markov property, expresses the independence of the future behavior of ξ(t), t ≥ s, from its past prior to s, given the current state ξ(s) = x. The conditional probabilities
p(s, x, t, B) = P{ξ(t) ∈ B|ξ(s) = x},
referred to as transition probabilities of a Markov process, describe the likelihood of the process moving from state ξ(s) = x to a state ξ(s) ∈ B, where B ⊆ R1. The corresponding function p(s, x, t, y), −∞ < y < +∞ is called the transition density. Accordingly, the states of failure-free operation and failure of mine ventilation fans can be described by these transition probabilities.
When assessing the reliability of complex technical systems, the methods of queuing theory are commonly employed, which generally involve studying steady-state regimes of simple ergodic systems [15, 16]. All failure flows that transfer such a system from an operable to an inoperable state are simple and therefore imply statistical independence of the constituent random events.
Consequently, verifying the statistical independence of failure flows is a prerequisite for applying continuous-time discrete Markov processes to evaluate the reliability of mine ventilation fans as elements of complex technical systems.
From probability theory, by definition, random variables ξ1, …, ξn are independent if the algebras Aξ1, …, Aξn generate by them are independent. Since each algebra Aξ1 consists of events of the form {ξi = B}, B ⊆ R1, this is equivalent to stating that random variables are independent if, for any sets Bi
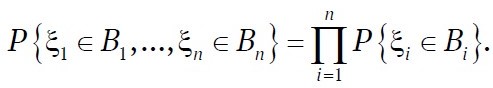
According to a well-known theorem in probability theory, the independence of algebras Aξ1, …, Aξn is equivalent to the independence of the partitions αξ1, …, αξn generating them. This yields another equivalent definition: random variables ξ1, …, ξn are independent if, for any sets x1j1, …, xnjn
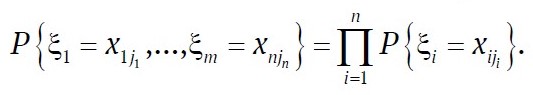
The covariance (or correlation moment) of two random variables ξ and η is defined as
cov (ξ, η) = μξ,η = M(ξ – M(ξ))(η – M(η)), (1)
and it follows directly that cov (ξ, η) = M(ξη) – M(ξ)M(η). Equation (1) can also be expressed as
![]()
where F(x, y) the joint cumulative distribution function of the two-dimensional random vector (ξ, η). In particular, if (ξ, η) has density p(x, y), then
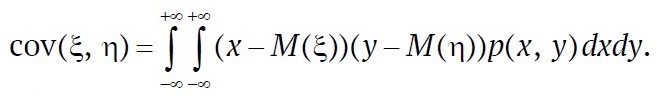 Covariance is used as a measure of dependence between random variables. This is justified by the well-known equality in probability theory, cov (ξ, η) = 0, which holds for independent random variables ξ and η with finite variances. However, the value of the covariance of ξ and η depends on the choice of measurement units for these variables, and therefore this characteristic is not always convenient to use. Free from this drawback is the characteristic known as the correlation coefficient. By definition, the correlation coefficient of random variables ξ and η is the ratio of their covariance to the product of their standard deviations:
Covariance is used as a measure of dependence between random variables. This is justified by the well-known equality in probability theory, cov (ξ, η) = 0, which holds for independent random variables ξ and η with finite variances. However, the value of the covariance of ξ and η depends on the choice of measurement units for these variables, and therefore this characteristic is not always convenient to use. Free from this drawback is the characteristic known as the correlation coefficient. By definition, the correlation coefficient of random variables ξ and η is the ratio of their covariance to the product of their standard deviations:
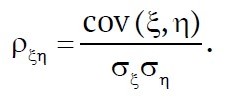 The operating conditions of mine ventilation fans give rise to both dependent and independent failures. For example, failures such as “impeller looseness on the shaft” and “bearing wear” are dependent. In contrast, “bearing wear” and “failure of the motor control system” are independent. Let ξ and η represent such failure events. Clearly, the correlation coefficient of independent random variables ξ and η equals zero, i.e., ρξη = 0 if ξ and η are independent. Random variables ξ and η are called uncorrelated if their correlation coefficient ρξη = 0. Thus, independence implies uncorrelatedness. The converse does not hold in general – specifically, when only second moments are known: cov (ξ, η) = 0 does not necessarily imply independence of ξ and η.
The operating conditions of mine ventilation fans give rise to both dependent and independent failures. For example, failures such as “impeller looseness on the shaft” and “bearing wear” are dependent. In contrast, “bearing wear” and “failure of the motor control system” are independent. Let ξ and η represent such failure events. Clearly, the correlation coefficient of independent random variables ξ and η equals zero, i.e., ρξη = 0 if ξ and η are independent. Random variables ξ and η are called uncorrelated if their correlation coefficient ρξη = 0. Thus, independence implies uncorrelatedness. The converse does not hold in general – specifically, when only second moments are known: cov (ξ, η) = 0 does not necessarily imply independence of ξ and η.
As an illustration, let ξ be a random variable with finite M(ξ3) and a density ρ(x) symmetric about х = 0 i.e., ρ(–x) = ρ(x). Define η = ξ2. Then
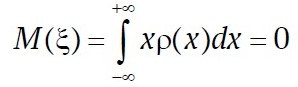
due to the evenness of ρ(x). It follows, by the evenness of ρ(x), that
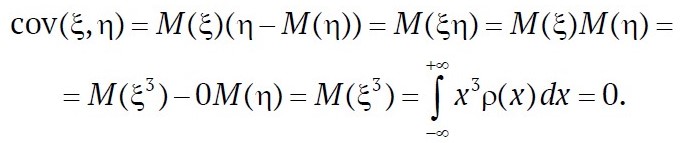
Nevertheless, ξ and η are dependent: if x is any number such that 0 < ρ(ǀξǀ < x) < 1, then for y = x2
ρ(ǀξǀ) < x, η < y) = ρ(ǀξǀ < x, ξ2 < x2) = ρ(ǀξǀ < x) > ρ2(ǀξǀ < x) = ρ(ǀξǀ < x)ρ(η < y).
Therefore, the uncorrelatedness of random events in a failure flow cannot serve as evidence of independence.
Moreover, even for correlated random variables with a bivariate normal distribution, the hypothesis of independence of random variables x and y in mathematical statistics [17] is tested using a sample (x, y), …, (xn, yn) of size n, based on reliability statistics of mine ventilation fans
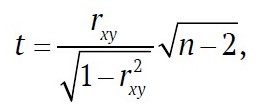
where
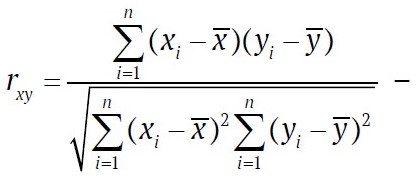 is the sample correlation coefficient, and
is the sample correlation coefficient, and
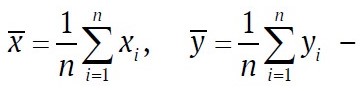 are sample means.
are sample means.
Using a two-tailed test at significance level α with m = n – 2 degrees of freedom, the null hypothesis H of independence of random failure probabilities is rejected if
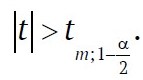 For the same distribution parameters, the hypothesis may be tested against critical values of the correlation coefficient. In this case, under a two-tailed test for significance level α and m = n – 2 degrees of freedom, H is rejected if |rxy| > rm;q.
For the same distribution parameters, the hypothesis may be tested against critical values of the correlation coefficient. In this case, under a two-tailed test for significance level α and m = n – 2 degrees of freedom, H is rejected if |rxy| > rm;q.
The critical values of the correlation coefficient are determined from statistical tables for m = n – 2 and q = 1– α/2.
Methods
In practical applications, verification of stochastic independence using the expressions described above is highly challenging. Consequently, an alternative explanation is often employed, although it is purely qualitative in nature: random variables ξ and η are defined as independent if the random mechanisms determining the distributions of ξ and η operate independently of one another [9].
Guided by this qualitative interpretation, in many cases the failures of individual components in mechanical systems cannot be regarded as independent events [18]. As an illustrative example, the operability of the assemblies of a main mine centrifugal ventilation fan VShTs-16 is considered.
The VShTs-16 fan is designed for mine ventilation in installations with bypass channels, operating in blowing or suction mode during shaft sinking, in heating and ventilation systems, for cooling electric machines, and for other industrial purposes. The fan is manufactured by AO AMZ Ventprom (Open Joint-Stock Company Artyomovsky Machine Engineering Plant VENTPROM).
The assemblies of the fan are subjected to disturbances in the air stream caused by unsteady aerodynamic forces arising from flow nonuniformity during interaction with the casing ribs and the blades of the guide and straightening devices [19]. Furthermore, variation in the mechanical loading on fan components is induced both by operational adjustment of the air supply into mine workings and by sudden pressure fluctuations resulting from abrupt changes in the characteristics of the external ventilation network, associated with the movement of equipment and personnel through airlock chambers and with the travel of conveyances in intake shafts [20]. Transient processes occurring in such complex mechanical systems exert a considerable influence both on the efficiency indicators of the units and on the reliability indicators of the system as a whole [21]. An analysis of the operational reliability of the fan under underground ore mining conditions, conducted by the authors, demonstrated that the unsteady nature of blade loading – caused by sudden gas outbursts or by pressure waves generated during blasting operations – results in a significant number of failures such as “impeller looseness on the shaft” and “bearing wear.”
Such failures lead to rotor imbalance, an increase in dynamic loads, and, consequently, accelerated bearing wear. Therefore, random events such as “impeller looseness on the shaft” and “bearing wear” cannot be considered stochastically independent. It is evident that reliance on such a qualitative criterion of statistical independence introduces significant uncertainty into the reliability analysis of mechanical systems. A definitive resolution of this issue can be achieved only through the application of rigorous quantitative criteria. In scientific and engineering practice, correlation analysis, as described in the theoretical section of this paper, is widely used to evaluate the dependence of random variables.
Accordingly, in the case of a normal distribution, even correlated random variables may, under the stated hypothesis, be regarded as independent.
It should be emphasized, however, that this approach is applicable only to a limited class of mechanical systems, since the normal distribution of failure flows is characteristic primarily of designs that are well optimized for reliability, i.e., exhibiting a high level of operational durability. For the components and mechanisms of such systems, gradual failures – wear, fatigue, corrosion, etc. – predominate over sudden failures. The majority of mining machines and stationary mine equipment cannot be attributed to this class due to the insufficiently high technical level of mining machine-building and, in particular, the severe conditions of their operation and maintenance.
For main mine ventilation fans, the failure-free operating time of mechanical components approximately follows the Gnedenko–Weibull distribution with parameters a = 800, b = 1.31, as well as its particular cases, the Rayleigh and exponential distributions with parameter ω = 0.264. For centrifugal main mine ventilation fans, the logarithmic-normal distribution provides a more accurate description of the failure flow [12]. According to an analysis of the operational reliability of the VShTs-16 main mine centrifugal ventilation fan performed by the Artemovsk Machine-Building Plant, the probability of failure-free operation of these units at the Sibay and Uchaly mining and processing plants corresponds closely, under the Mises criterion (ω2 = 2.38–3.64), to the exponential distribution (ω2 = 0.466-0.747∙10−4). Thus, statistical evaluation of stochastic independence in failure flows of mining machines and stationary mine equipment using sample correlation coefficients is, in most cases, infeasible. For such systems, nonparametric statistical methods, including Fisher’s exact test and the χ2 test, may be applied. In addition to their main advantage – the ability to be used under any distribution law – nonparametric methods, unlike correlation analysis, do not require large volumes of prior failure data and can be applied at the earliest (preliminary) stages of reliability analysis.
An analysis of the above example of testing the independence of the failures “impeller looseness on the shaft” and “bearing wear,” performed using the χ2 independence test, confirmed the validity of the conclusion previously drawn from the qualitative evaluation of the physical mechanism. The hypothesis H of independence of these failures was tested using a contingency table of attributes (Table 1).
Table 1
Contingency of attributes for the independence hypothesis
j → i | 1 → 2 | hj |
1 2 | 16 → 1 3 → 8 | 17 11 |
hi | 19 → 9 | 28 |
The test statistic for the 2×2 contingency case is calculated using the following formula
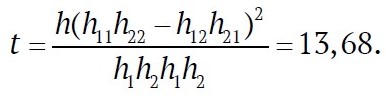
For a significance level of α = 0.05 and degrees of freedom m = (r − 1)(s − 1) – (2 − 1)(2 − 1) = 1, the tabulated critical value of χ2 is . Since the calculated value t = 13.68 exceeds this threshold, hypothesis H must be rejected. This indicates that the failures of the VShTs-16 main mine centrifugal ventilation fan – specifically, “impeller looseness on the shaft” and “bearing wear” – are stochastically dependent events.
Up to this point, the discussion has focused on the limitation of applying Markov processes to reliability analysis under the assumption of stochastic independence of failures. To address the possibility of stochastic dependence between failures of components in mechanical systems, Prof. A.S. Pronikov proposed a classification of complex technical systems from the perspective of reliability, distinguishing three categories: disjoint, dependent, and combined systems [18].
Disjoint systems are those in which the reliability of individual elements can be determined in advance, since the failure of an element can be regarded as an independent event. Such systems are more typical of radio electronics, where individual components – semiconductor devices, resistors, capacitors, etc. – perform independent functions and must ensure output parameters within specified limits regardless of the parameters of other components. Replacement of a failed element fully restores the operability of the entire system.
Dependent systems are those in which element failures are dependent events associated with changes in the output parameters of the system as a whole. For example, the reliability of a mechanical system designed for precise displacement of a driven link depends on the wear resistance of all components transmitting motion. However, the wear of each component cannot be limited independently of the others, since greater wear of one component may be compensated by the higher wear resistance of another.
Combined systems consist of subsystems with internally dependent structures but with independence between the subsystems themselves.
Although simplified, this classification of complex technical system structures makes it possible to select suitable methodological approaches for analyzing overall reliability and, in particular, for applying Markov process theory.
For systems with disjoint structures, the assumption of stochastic independence in failure flows of elements is valid, and the use of Markov methods is not constrained. By contrast, in mechanical systems with dependent structures, the applicability of Markov process theory is limited.
For complex technical systems with combined structures, the Markov approach is acceptable, with a certain approximation, only for analyzing reliability at the highest level, i.e., when the system is studied as an aggregate of subsystems.
It should be emphasized that these observations apply to the analysis of functional reliability, in which element failure is understood as a breakdown or malfunction that results in system failure, i.e., cessation of operation.
In the case of parametric reliability, where element failure is defined as the deviation of its functional characteristic beyond permissible limits – leading to the system’s main parameters falling outside the allowable range – the use of any assumptions based on stochastic independence of the studied failure flows is inadmissible. This is particularly important for mining machines and stationary mine equipment, which, as systems of high material intensity and large unit power, are highly sensitive to the stability of their basic parameters during operation.
Experimental studies
As an illustrative example, the operation of the VShTs-16 main mine centrifugal ventilation fan is considered under the assumption of no stochastic dependence in the failure flows. In this case, the probability of system failure does not depend on time or on previous states [22]. The system is assumed to exist within a single day in one of two states: operable, P1(t), or inoperable, F1(t). This two-state representation simplifies the analysis and enables estimation of transition probabilities between states.
Based on observed transitions over a time interval t, the probabilities can be expressed as a transition matrix

For the VShTs-16 fan, the probability of remaining operable during a given period (P11) is 0.9, and the probability of transitioning to failure (P12) is 0.1. The probability of recovery during the period (P21) is taken as 0.99, while the probability of non-recovery (P22) is 0.01. Taking these values into account, matrix (2) becomes
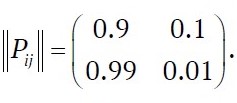 The state diagram of the system, illustrating possible transitions between operable and inoperable states, is shown in Fig. 1.
The state diagram of the system, illustrating possible transitions between operable and inoperable states, is shown in Fig. 1.
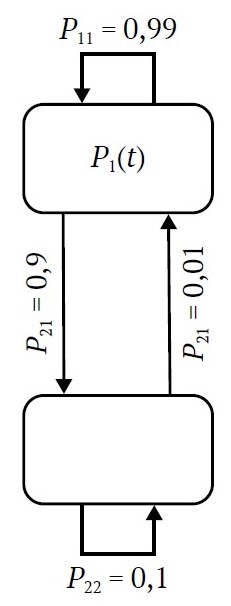
Fig. 1. State diagram of the system (VShTs-16)
Let the vector of initial state probabilities be defined as
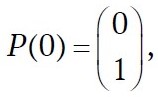
then, for a homogeneous Markov chain, the probabilities of system states can be determined from the relation:
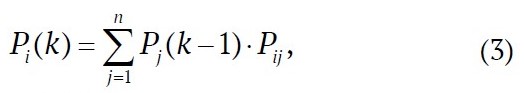 where k is the step number (months).
where k is the step number (months).
From expressions (1) and (2), the probability of failure-free operation in the first month is P1(1) = P1(0) ∙ P11 + P2(0) ∙ P21 = 0.99, and the probability of failure is P1(1) = P1(0) ∙ P12 + P2(0) ∙ P22 = 0.01. In the second month, the probability of failure-free operation is 0.9009, while the probability of failure is 0.0991. Subsequently, by applying computer modeling of the probabilistic process, the data obtained for several cycles (months) are presented in tabular form (Table 2).
Table 2
Simulation results
t, months | P1(t) | F1(t) | t, months | P1(t) | F1(t) |
1 | 0.99 | 0.01 | 6 | 0.90826 | 0.09174 |
2 | 0.9009 | 0.099 | 7 | 0.90826 | 0.09174 |
3 | 0.9089 | 0.091 | 8 | 0.90826 | 0.09174 |
4 | 0.9081 | 0.0918 | 9 | 0.90826 | 0.09174 |
5 | 0.9082 | 0.09173 | 10 | 0.90826 | 0.09174 |
Discussion
Analysis of the obtained values indicates that this approach is generally straightforward to apply; however, it does not account for the cumulative effect of failures associated with system degradation [23]. Nevertheless, system reliability can be evaluated by applying formula (3), supplemented with stochastic coefficients K(t) derived from the distribution laws of reliability indicators as functions of operating time t: P = f{Pi(k), K(t)}.
Table 3
Simulation results with stochastic coefficients K(t)
t, months | P1(t) | t, months | P1(t) |
1 | 0.98910 | 6 | 0.90286 |
2 | 0.89910 | 7 | 0.90196 |
3 | 0.90622 | 8 | 0.90106 |
4 | 0.90460 | 9 | 0.90016 |
5 | 0.90376 | 10 | 0.89926 |
Table 3 shows the calculated probability of the VShTs-16 system remaining in an operable state, taking into account coefficients that reflect the degradation process of the technical system. It should be noted, however, that this calculation does not incorporate the frequency of random failures or the effect of individual component failures on overall system reliability.
The corresponding simulation results are illustrated graphically in Fig. 2.
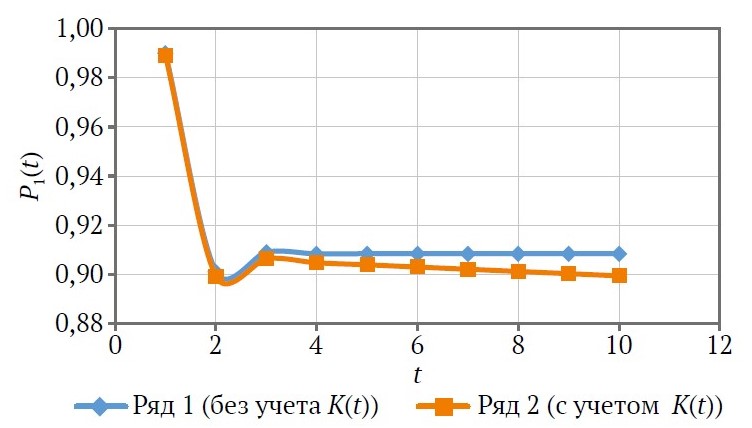 Fig. 2. Probability of the VShTs-16 remaining in an operable state over time
Fig. 2. Probability of the VShTs-16 remaining in an operable state over time
Analysis of the dependence shown in Fig. 2 (series 2) indicates that the probability of the system remaining in an operable state decreases with increasing operating period and exhibits a nonlinear character. Thus, the qualitative determination of failure probability reduces to refining the stochastic coefficients.
Conclusions
The application of homogeneous Markov process models has inherent limitations, since the transition intensities between system states are not always constant. When transition intensities vary with time, calculations become significantly more complex, and in some cases certain intensities may not exist at all. In such situations, it is impossible to construct a system of differential equations with time-dependent coefficients. In mechanical systems, such dynamic transition intensities are typically associated with aging processes.
The analysis of the operational reliability of the VShTs-16 main mine centrifugal ventilation fan showed that the probability of failure-free operation of these units at the Sibay and Uchaly mining and processing plants corresponds closely, according to the Mises criterion (ω2 = 2.38–3.64), to the exponential distribution (ω2 = 0.466–0.747∙10−4). Verification of the independence of the failures “ impeller looseness on the shaft” and “bearing wear,” performed using the independence test, did not confirm the independence hypothesis, since the calculated value t = 13.68 exceeded the tabulated critical value of 3.84. This finding demonstrates that the failures of the VShTs-16 fan are stochastically dependent events.
To account for the influence of individual component failures on overall system failure, the determination of failure probability should incorporate refined stochastic coefficients. This approach may provide a foundation for developing methodological principles for monitoring and diagnosing the technical condition of ventilation systems, as well as for predicting the residual service life of operating fans based on condition monitoring data.
In this context, the analysis of reliability may involve finite Markov chains and semi-Markov processes. When stochastic dependence is present in the failure flows of mechanical systems, the use of Markov process theory remains possible, but the most effective tool for reliability analysis under such conditions is the Monte Carlo numerical simulation method [24].
References
1. Ahaiev R., Prytula D., Kliuiev E., et al. The determination of the influence degree of mining-geological and mining-technical factors on the safety of the degassing system. In: E3S Web of Conferences. II International Conference Essays of Mining Science and Practice. 2020;168:00040. https://doi.org/10.1051/e3sconf/202016800040
2. Materova E. S., Aksenova Zh. A., Nikiforov A. A., et al. Development potential of the mining sector in the Russian Federation. Ugol’. 2024;(12):41–46. (In Russ.) http://dx.doi.org/10.18796/0041-5790-2024-12-41-46
3. Balovtsev S. V. Assessment of ventilation circuits with regard to geological and geotechnical conditions of coal seam mining. Mining Informational and Analytical Bulletin. 2019;(6):173–183. https://doi.org/10.25018/0236-1493-2019-06-0-173-183
4. Chen Y., Liu R., Liu C., et al. Influence of blade installation angle spanwise distribution on the energy characteristics of mining contra-rotating axial flow fan. Scientific Reports. 2025;15(1):6444. https://doi.org/10.1038/s41598-025-90797-4
5. Kaledina N. O., Malashkina V. A. Indicator assessment of the reliability of mine ventilation and degassing systems functioning. Journal of Mining Institute. 2021;250:553–561. https://doi.org/10.31897/PMI.2021.4.8
6. Odeyar P., Apel D. B., Hall R., et al. A review of reliability and fault analysis methods for heavy equipment and their components used in mining. Energies. 2022;15(17):6263. https://doi.org/10.3390/en15176263
7. Ushakov V. K. Reliability and efficiency of mine ventilation. Mining Informational and Analytical Bulletin. 2015;(4):240–248. (In Russ.)
8. Kashnikov A. V., Kruglov Yu. V. Fuzzy logic-based determination of ventilation parameters in active mining areas. Mining Informational and Analytical Bulletin. 2023;(5):68–82. (In Russ.) https://doi.org/10.25018/0236_1493_2023_5_0_68
9. Reinschke K. Zuverlässigkeit und verfügbarkeit technischer systeme: theorie – praxis – berechnung. Berlin: VEB Verlag Technik; 1973. 392 p. (In German) (Trans. ver.: Reinschke K. Reliability and availability of technical systems: theory – practice – calculation. Moscow: Mir Publ. House; 1979. 452 p. (In Russ.))
10. Petrochenkov A. B., Bochkarev S. V., Romodin A. V., Eltyshev D. K. Planning of electrical equipment operation process using Markov chain theory. Elektrotekhnika. 2011;(11):20–24. (In Russ.)
11. Agbinya J. I. Markov Chain and its applications. In: Applied Data Analytics – Principles and Applications. 1st ed. New York: River Publishers eBooks; 2022. 15 p. https://doi.org/10.1201/9781003337225-1
12. Ssempijja M. N., Namango S., Ochola J., Mubiru P. K. Application of Markov Chains in manufacturing systems: a review. International Journal of Industrial Engineering and Operational Research. 2021;3(1):1–13. https://doi.org/10.22034/ijieor.v3i1.26
13. Wang Y., Xie B., E Sh. Adaptive relevance vector machine combined with Markov-chain-based importance sampling for reliability analysis. Reliability Engineering & System Safety. 2022;220:108287. https://doi.org/10.1016/j.ress.2021.108287
14. Rozanov Yu. A. Introduction to the theory of random processes. Moscow: Nauka; 1982. 128 p. (In Russ.)
15. Ignatov V. A., Manshin G. G., Kostanovsky V. V. Elements of optimal maintenance theory for technical devices. Minsk: Nauka i Tekhnika; 1974. 192 p. (In Russ.)
16. Ovcharov L. A. Applied problems of queueing theory. Moscow: Mashinostroenie; 1969. 324 p. (In Russ.)
17. Müller P., Neumann P., Storm R. Tafeln der mathematischen statistik. Berlin: VEB Deutscher Verlag der Wissenschaften; 1979. 272 s. (In German) (Trans. ver.: Müller P., Neumann P., Storm R. Tables of mathematical statistics. Moscow: Finansy i Statistika; 1982. 272 p. (In Russ.))
18. Pronikov A. S. Reliability of machines. Moscow: Mashinostroenie; 1978. 592 p. (In Russ.)
19. Russky E. Yu. Research of vibration reliability of axial fans rotors of the mine main airing. Interexpo GEO-Siberia. 2017;2(2):121–125. (In Russ.)
20. Kopachev V. F. Rationale for main fans service life in the conditions of changing load. Izvestiya Vysshikh Uchebnykh Zavedenii. Gornyi Zhurnal. 2020;(6):102–108. (In Russ.) https://doi.org/10.21440/0536-1028-2020-6-102-108
21. Kopachev V. F., Kopacheva E. A. Effect of transient processes on technical performance of compressed air production and handling systems in mines. Mining Informational and Analytical Bulletin. 2025;(1–1):106–119. https://doi.org/10.25018/0236_1493_2025_11_0_106
22. Ushakov V. K. Mathematical modeling of reliability and efficiency of mine ventilation systems. Moscow: Gornaya Kniga; 2003. 181 p. (In Russ.)
23. Potapov V. D., Prizyov A. D. Simulation modeling of production processes in mining industry. Moscow: Vysshaya Shkola; 1981. 191 p. (In Russ.)
24. Jones G. L., Qin Q. Markov chain Monte Carlo in practice. Annual Review of Statistics and Its Application. 2022;9(1):557–578. https://doi.org/10.1146/annurev-statistics-040220-090158
About the Authors
P. V. VyatkinRussian Federation
Pavel V. Vyatkin – General Director
Artemovsky
N. G. Valiev
Russian Federation
Niyaz G. Valiev – Dr. Sci. (Eng.), Professor, Head of the Department of Mining Engineering
Yekaterinburg
Scopus ID 55749527900
AuthorID 284710
D. I. Simisinov
Russian Federation
Denis I. Simisinov – Dr. Sci. (Eng.), Associate Professor, Head of the Department of Mining Equipment Operation
Yekaterinburg
Scopus ID 6505975115
AuthorID 435571
E. B. Volkov
Russian Federation
Evgenii B. Volkov – Cand. Sci. (Eng.), Associate Professor, Head of the Department of Technical Mechanics
Yekaterinburg
Scopus ID 57220450540
AuthorID 795310
Review
For citations:
Vyatkin P.V., Valiev N.G., Simisinov D.I., Volkov E.B. Reliability analysis of mine ventilation fans based on Markov process theory. Mining Science and Technology (Russia). 2025;10(3):289-297. https://doi.org/10.17073/2500-0632-2025-03-401




































