Исследование надежности шахтных вентиляторов на основе теории марковских процессов

Введение

Аэрологические факторы риска при подземной добыче полезных ископаемых по данным Ростехнадзора остаются на высоком уровне. При переходе предприятий на подземную разработку в сложных горно-геологических и горнотехнических условиях и увеличении глубины производства горных работ на действующих рудниках требования к эффективности вентиляционно-дегазационных систем возрастают [1–3]. Важнейшую роль в аэрологических системах играет безотказность шахтных вентиляторных установок.

Надежность шахтных вентиляторных установок определяется комплексом различных геологических, горнотехнологических и конструктивных факторов преимущественно стохастического характера [4, 5].

Задача определения количественных показателей надежности шахтных вентиляторных установок решается с применением различных математических методов моделирования случайных процессов. Впервые основные понятия и показатели надежности ШВС были предложены в следующих методах: метод функции состояния, метод критических путей, статистический метод и метод статистического моделирования [6, 7], нечеткой логики [8].

Математический аппарат теории надежности достаточно многообразен, но ведущее положение в нем, несомненно, занимают математическая статистика, теория вероятностей и теория случайных процессов. Концепция надежности сложных технических систем обусловила широкое применение в качестве математического метода теории марковских процессов. Подобный подход успешно используется при анализе работоспособности сложных электронных устройств и систем [9, 10]. Следует отметить, что и сама теория надежности как общетехническая дисциплина сформировалась прежде всего под влиянием развития радиоэлектроники, вычислительной и ракетной техники, хотя впервые вопросы надежности были поставлены в 1930-е годы специалистами в области строительной механики и систем энергетики. Именно поэтому самое широкое использование в теории надежности нашли те математические методы, возможности которых удовлетворяли требованиям задач, поставленных вычислительной техникой.

Анализ работоспособности механических систем как второе направление развития общей теории надежности изделий начал формироваться несколько позднее. Математический инструментарий этой области надежности в значительной степени пополнялся за счет методов и теорий, получивших глубокое развитие и нашедших широкое практическое применение в электронике. В некоторых случаях такое заимствование проводилось и проводится без учета специфики исследуемых объектов, без достаточно основательного анализа физики отказов. Сказанное можно с успехом отнести и к анализу надежности механических систем с помощью теории марковских процессов. В работах [11–13] авторы используют теорию марковских процессов при разработке методик инженерных расчетов показателей надежности конкретных изделий машиностроения и технологических процессов их производства.

Теория

По определению [14] марковским процессом называется случайный процесс ξ(t), t ≥ t₀, обладающий свойством

p(s, x, t, B) = P{f(s, x, t) ∈ B}, B ⊆ R¹, t ≥ S,

при условии

ξ(s₁) = x₁, …, ξ(s_m) = x_m, ξ(s) = x,

независимо от х₁, х₂, … х_m.

Это свойство, называемое марковским свойством случайного процесса, выражает независимость поведения процесса ξ(t), t ≥ s в «будущем» от его «прошлого» до момента s при фиксированном (известном) «текущем» состоянии ξ(s) = x. Условные вероятности

p(s, x, t, B) = P{ξ(t) ∈ B|ξ(s) = x},

называемые переходными вероятностями марковского процесса, задают вероятности перехода процесса из исходного состояния ξ(s) = x в то или иное состояние ξ(s) ∈ B из множества B ⊆ R¹. Соответствующая плотность p(s, x, t, y), −∞ < y < +∞ называется переходной плотностью. Соответственно, состояния безотказной работы и отказа шахтных вентиляторных установок могут быть описаны указанными переходными вероятностями.

Используемые при анализе надежности сложных технических систем методы теории массового обслуживания предполагают, как правило, изучение стационарных режимов работы простейших эргодических систем [15, 16]. Все потоки отказов, переводящие такую систему из работоспособного в неработоспособное состояние, являются простейшими и, следовательно, предусматривают статистическую независимость составляющих случайных событий.

Таким образом, исследование статистической независимости потока отказов является необходимым условием при анализе вопроса о применимости дискретных марковских процессов с непрерывным временем для оценки надежности шахтных вентиляторных установок как объектов сложных технических систем.

Из теории вероятностей по определению случайные величины ξ₁, …, ξ_n называются независимыми, если порожденные ими алгебры A_ξ1, …, A_ξn независимы. Поскольку каждая из алгебр  A_ξn состоит из событий вида {ξ_i = B}, B ⊆ R¹, то приведенное определение эквивалентно следующему: случайные величины независимы, если для любых числовых множеств B_i

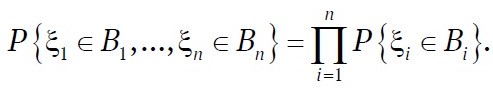На основании известной теоремы теории вероятностей следует, что независимость алгебр A_ξ1, …, A_ξn  равносильна независимости порождающих их разбиений α_ξ1, …, α_ξn . Это приводит еще к одному эквивалентному определению независимости: случайные величины ξ₁, …, ξ_n независимы, если для любых x_1j1, …, x_njn,

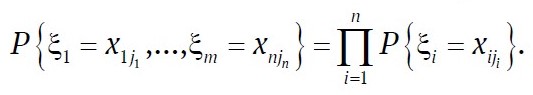Согласно определению ковариация (корреляционный момент) случайных величин ξ и η равна

         cov (ξ, η) = μ_ξ,η = M(ξ – M(ξ))(η – M(η)),          (1)

в частности, непосредственно из этого определения следует, что cov (ξ, η) = M(ξη) – M(ξ)M(η). Тогда выражение (1) можно записать как

где F(x, y) – функция распределения двумерной случайной величины (ξ, η). В частности, если эта случайная величина обладает плотностью p(x, y), то

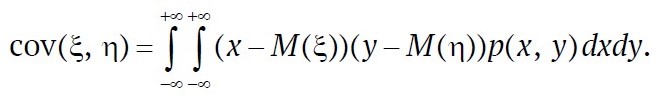Ковариацию используют в качестве меры зависимости случайных величин, что оправдывается известным в теории вероятностей равенством cov (ξ, η) = 0 для независимых случайных величин ξ и η с конечными дисперсиями. Отметим, что величина ковариации ξ и η зависит от выбора единиц измерения этих величин, поэтому использовать эту характеристику не всегда удобно. От такого недостатка свободна характеристика, называемая коэффициентом корреляции. По определению, коэффициентом корреляции случайных величин ξ и η называется отношение их ковариации к произведению их средних квадратичных отклонений:

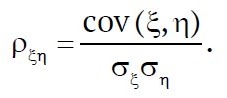
Условия работы шахтных вентиляторных установок приводят как к зависимым, так и независимым отказам. К примеру, отказы типа «люфт рабочего колеса на валу», «износ опорных подшипников» будут зависимыми. Независимыми – «износ опорных подшипников» и отказ системы управления электродвигателем. Указанные события, приводящие к отказам, оценим случайными величинами ξ и η. Очевидно, что коэффициент корреляции независимых случайных величин ξ и η равен нулю, т. е. ρ_ξη = 0, если ξ и η независимы. Случайные величины ξ и η называются некоррелированными, если их коэффициент корреляции ρ_ξη = 0. Таким образом, из независимости следует некоррелированность. Утверждение, обратное данному свойству в широком смысле, т.е. в условиях известности только вторых моментов случайных величин, неверно, т.е. если cov (ξ, η) = 0, то величины и ξ и η не обязательно независимы.

Рассмотрим пример таких величин.

Пусть ξ – случайная величина с конечным M(ξ³), обладающая симметричной относительно точки х = 0 плотностью ρ(x), т.е. ρ(–x) = ρ(x). Обозначим η = ξ². Тогда

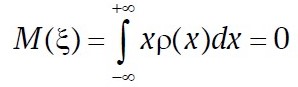
в силу четности функции ρ(x). Поэтому также на основании четности ρ(x)

.

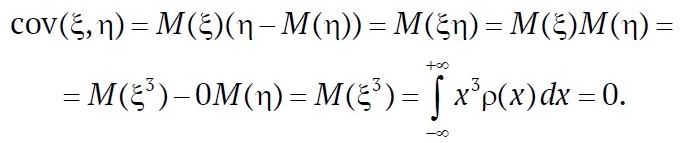В то же время ξ и η зависимы: если x – любое число, для которого 0 < ρ(ǀξǀ < x) < 1, то при y = x²

ρ(ǀξǀ) < x, η < y) = ρ(ǀξǀ < x, ξ² < x²) = ρ(ǀξǀ < x) > ρ²(ǀξǀ < x) = ρ(ǀξǀ < x)ρ(η < y).

Следовательно, некоррелированность случайных событий в потоке не может служить основанием для утверждений о независимости.

Более того, даже для коррелированных случайных величин, имеющих двумерное нормальное распределение, гипотеза о независимости случайных величин x и y в математической статистике [17] проверяется по результатам выборки (x, y), …, (x_n, y_n) объемом n с помощью статистики об отказах шахтных вентиляторных установок

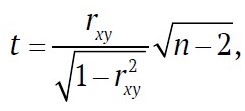
где  

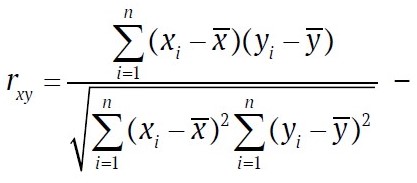
выборочный коэффициент корреляции;

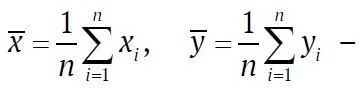
выборочные средние.

При применении критерия (двустороннего) на уровне значимости α с m = n – 2 степенями свободы гипотеза Н о независимости случайных вероятностей отказов отвергается, если

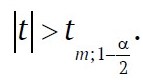
Для тех же параметров распределения указанную гипотезу можно проверить, используя критические значения коэффициента корреляции, в этом случае при применении (двустороннего) критерия на уровне значимости α для m = n – 2 степеней свободы гипотеза Н отвергается, если |r_xy| > r_m;q.

Критические значения коэффициента корреляции определяются по таблицам для m = n – 2 и q = 1– α/2.

Методы

На практике проверку стохастической независимости с помощью описанных выражений провести весьма затруднительно. Поэтому чаще всего пользуются другим пояснением, которое, однако, носит чисто качественный характер, а именно случайные величины ξ и η называются независимыми, если случайные механизмы, определяющие распределение ξ и η, протекают независимо друг от друга [9].

Руководствуясь сформулированным выше качественным соображением в ряде случаев для механических систем отказы отдельных элементов нельзя считать независимыми событиями [18]. В качестве примера, подтверждающего это положение, рассмотрим работоспособность узлов вентилятора шахтного центробежного главного проветривания ВШЦ-16.

Вентилятор ВШЦ-16 предназначен для проветривания шахт (рудников) в установке с обводными каналами, работая в режиме нагнетания или всасывания при проходке стволов шахт, в системах отопления и вентиляции, для охлаждения электрических машин и в других промышленных целях. Завод-изготовитель вентилятора – АО «Артемовский машиностроительный завод «ВЕНТПРОМ».

На узлы вентилятора действуют возмущения от воздушного потока, вызванные действием нестационарных аэродинамических сил, возникающих вследствие неравномерности течения потока при взаимодействии с ребрами корпуса, лопатками направляющего и спрямляющего аппаратов [19]. Также следует отметить изменение механической нагрузки на элементы вентилятора, обусловленное как оперативным регулированием подачи воздуха в горные выработки, так и внезапными колебаниями давления при скачкообразных изменениях характеристик внешней вентиляционной сети, связанной с проходами техники и людей через шлюзовые камеры и перемещением сосудов по воздухоподающим стволам [20]. Переходные процессы, происходящие в сложных механических системах, значительно влияют как на технические показатели экономичности установок, так и на показатели надежности функционирования всей системы в целом [21]. Анализ эксплуатационной надежности вентилятора при работе в условиях подземной разработки рудных месторождений полезных ископаемых, проведенный авторами, показал, что нестационарный характер нагружения лопаточных венцов, вызванный внезапными выбросами газа или набегающими волнами давления, образованными проводимыми взрывными работами, обусловливают появление значительного количества отказов типа «люфт рабочего колеса на валу», «износ опорных подшипников».

Подобные отказы приводят к нарушению балансировки ротора, увеличению динамических нагрузок и, следовательно, значительному возрастанию степени износа опорных подшипников. Таким образом, случайные события – отказы «люфт рабочего колеса на валу» и «износ опорных подшипников» – нельзя считать стохастически независимыми. Очевидно, что применение приведённой качественной оценки статистической независимости вносит существенную неопределённость в анализ надёжности механических систем. Однозначное решение вопроса может быть получено только на основании применения четких количественных критериев. В научной и инженерной практике для оценки зависимости случайных величин широко используется корреляционный анализ, описанный в теоретической части статьи.  

Таким образом, в случае нормального распределения даже коррелированные случайные величины при использовании указанной гипотезы могут оказаться независимыми.  

Отметим, что подобная методика оценки применима лишь к анализу ограниченного числа механических систем, т.к. нормальный закон распределения потока отказов характерен лишь для конструкций, хорошо отработанных на надежность, т. е. с высоким уровнем надежности. Для узлов и механизмов таких изделий наблюдается явное преобладание постепенных, т.е. износных, усталостных, коррозионных и т.д. отказов над внезапными. Большая часть горных машин и шахтных стационарных установок не могут быть отнесены к указанному классу из-за недостаточно высокого технического уровня горного машиностроения и, в особенности, тяжелых условий их эксплуатации и технического обслуживания.

Так, например, для шахтных вентиляторных установок главного проветривания время безотказной работы механических частей приближено к закону Гнеденко–Вейбулла с параметрами a = 800, b = 1,31 и частным случаям этого закона: релеевскому и экспоненциальному с параметром ω = 0,264. Для центробежных вентиляторов главного проветривания шахт более справедлив логарифмически-нормальный закон распределения потока отказов [12]. Анализом эксплуатационной надежности вентилятора шахтного центробежного главного проветривания ВШЦ-16, проведенным Артемовским машиностроительным заводом, установлено, что вероятность безотказной работы этих агрегатов на Сибайском и Учалинском горно-обогатительных комбинатах хорошо согласуется по критерию Мизеса ω² = 2,38–3,64 и c экспоненциальным законом распределения ω² = 0,466-0,747∙10⁻⁴. Таким образом, статистическая оценка стохастической независимости в потоках отказов горных машин и шахтных стационарных установок с помощью выборочных коэффициентов корреляции в большинстве случаев оказывается невозможной, для них можно применять критерии непараметрической статистики критерия точной вероятности Фишера и χ². Помимо основного достоинства – возможности применения при любых законах распределения, методы непараметрической статистики в отличие от корреляционного анализа не требуют наличия большого объема априорной информации об отказах, а также могут быть использованы на самых первых (предварительных) стадиях статического анализа надежности.

Анализ рассмотренного выше примера проверки независимости отказов «люфт рабочего колеса на валу» и «износ опорных подшипников», проведенный с помощью критерия независимости χ², подтвердил справедливость вывода, сделанного на основании качественной оценки физической картины. Гипотеза Н о независимости этих отказов проверялась по таблице сопряженности признаков (табл. 1).

Таблица 1

Сопряженность признаков гипотезы

Статистика для определения критерия в случае размерности матрицы сопряженности признаков 2×2 вычисляется по формуле

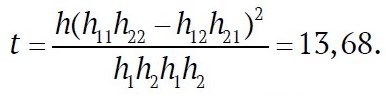
Для уровня значимости α = 0,05 и числа степеней свободы m = (r − 1)(s − 1) – (2 − 1)(2 − 1) = 1 табличная величина критического значения χ² составляет . Так как t = 13,68 > 3,84, гипотезу Н следует отвергнуть, т.е. отказы вентилятора шахтного центробежного главного проветривания ВШЦ-16 типа «люфт рабочего колеса на валу» и «износ опорных подшипников» являются стохастически зависимыми событиями.

До сих пор говорилось об ограничении применимости марковских процессов к анализу теории надежности по условию стохастической независимости отказов. Учитывая возможность стохастической зависимости устройств между отказами элементов механических устройств, проф. А. С. Проников предлагает следующую классификацию сложных технических систем с позиции надежности: расчлененные, связанные и комбинированные [18].

К расчлененным можно отнести такие сложные технические системы, у которых надежность отдельных элементов может быть заранее определена, т. к. отказ элемента можно рассматривать как независимое событие. Такие системы более характерны для радиоэлектроники, где отдельные элементы, выполненные в виде полупроводниковых приборов, сопротивлений, конденсаторов и т. д., имеют самостоятельные функции и должны обеспечивать значения выходных параметров в определенном диапазоне, независимо от параметров других элементов. Заменой отказавшего элемента полностью восстанавливается работоспособность всей системы;

К связанным относятся сложные технические системы, у которых отказ элементов является зависимым событием, связанным с изменением выходных параметров всей системы. Например, надежность работы механической системы, предназначенной для точного перемещения ведомого звена, зависит от износостойкости всех звеньев, передающих движение. Однако износ каждого звена не может быть лимитирован независимо от износа других звеньев, т. к. больший износ одного из них может компенсироваться высокой износостойкостью другого.

К комбинированным относятся сложные технические системы, состоящие из подсистем со связанной структурой и с независимостью между подсистемами.

Приведенная (достаточно условная) классификация структур сложных технических систем позволяет определить соответствующие методические подходы для анализа их надежности в целом и применения для этого теории марковских процессов в частности.

Так, для систем с расчлененными структурами ограничение применимости этих методов по условию стохастической зависимости в потоках отказов элементов очевидно несостоятельно. Для механических систем со связанными структурами использование теории марковских процессов ограничено.

Для сложных технических систем с комбинированными структурами марковский подход приемлем с известным приближением лишь для анализа надежности на высшем уровне, т. е. при изучении системы как совокупности подсистем.

Отметим, что все вышесказанное справедливо при анализе надежности функционирования (функциональной надежности), когда под отказом элемента понимается его поломка или выход из строя, приводящий к отказу всей системы, т. е. прекращению ее функционирования.

В смысле параметрической надежности, когда под отказом элемента понимается выход его функциональной характеристики за пределы допустимых значений и тем самым вывод из диапазона допустимых изменений основных параметров системы, использование любых положений, основанных на стохастической независимости исследуемых потоков отказов, недопустимо. Это замечание тем более важно, что для горных машин и шахтных стационарных установок как объектов с огромной материалоемкостью и удельной единичной мощностью значение вопросов стабильности основных параметров в процессе эксплуатации чрезвычайно велико.

Экспериментальные исследования

В качестве примера рассмотрим процесс функционирования системы – вентилятора шахтного центробежного главного проветривания ВШЦ-16 без стохастической зависимости в потоках отказов. Это означает, что вероятность отказа системы не зависит от времени и предыдущих состояний [22]. Предположим, что в течение одних суток система может находиться в одном из двух состояний: работоспособном – P₁(t) или неработоспособном – F₁(t). Такое представление позволяет упростить анализ работы системы и оценить вероятность перехода из одного состояния в другое.

После сбора данных о переходах системы из одного состояния в другое за промежуток времени t можно представить вероятности этих переходов в виде матрицы:

Предположим, что вероятность безотказной работы в заданное время вентилятора ВШЦ-16 (P₁₁) равна 0,9. Вероятность перехода из состояния отказа (P₁₂) составит 0,1. Вероятность восстановления в заданное время (P₂₁) примем 0,99. Вероятность того, что вентилятор не будет восстановлен (P₂₂), соответственно 0,01. С учётом этих данных матрица (2) будет выглядеть следующим образом:

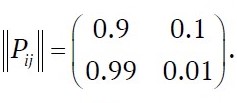
Граф состояний системы, иллюстрирующий возможные переходы между работоспособным и неработоспособным состояниями, представлен на рис. 1.

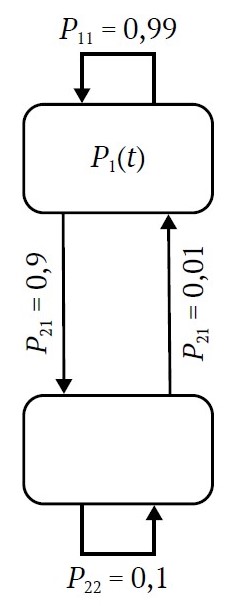
Рис. 1. Граф состояний системы (ВШЦ-16)

Зададим вектор начальных вероятностей состояний

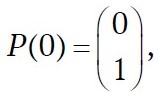
тогда для однородной марковской цепи вероятность состояний системы можно определить по формуле:

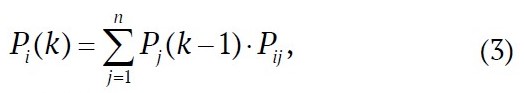
где k – номер шага, мес.

Исходя из выражений (1) и (2) вероятность безотказной работы в первый месяц равна P₁(1) = P₁(0) ∙ P₁₁ + P₂(0) ∙ P₂₁ = 0,99, а вероятность отказа – P₁(1) = P₁(0) ∙ P₁₂ + P₂(0) ∙ P₂₂ = 0,01. На второй месяц вероятность безотказной работы составляет 0,9009, а вероятность отказа – 0,0991. Далее, используя компьютерное моделирование вероятностного процесса, представим полученные данные за несколько циклов (мес) в виде таблицы (табл. 2).

Таблица 2

Результаты моделирования

Дискуссия

Анализируя полученные значения, заметим, что использование такого подхода обычно не вызывает принципиальных трудностей, но не учитывает накопительного эффекта отказов при деградации технической системы [23]. Тем не менее провести анализ надёжности системы можно, применив формулу (3), дополнив ее стохастическими коэффициентами K(t), полученными на основе законов распределения показателей надежности от наработки t: P = f{P_i(k), K(t)}.

Таблица 3

Результаты моделирования с учетом стохастических коэффициентов K(t)

В табл. 3 представлены результаты расчёта вероятности нахождения системы (ВШЦ-16) в работоспособном состоянии с учётом коэффициентов, отражающих процесс деградации технической системы. Важно отметить, что в данном расчёте не учитывались частота случайных отказов системы и влияние отказов отдельных элементов на отказ всей системы.

Результаты компьютерного моделирования в графической форме представлены на рис. 2.

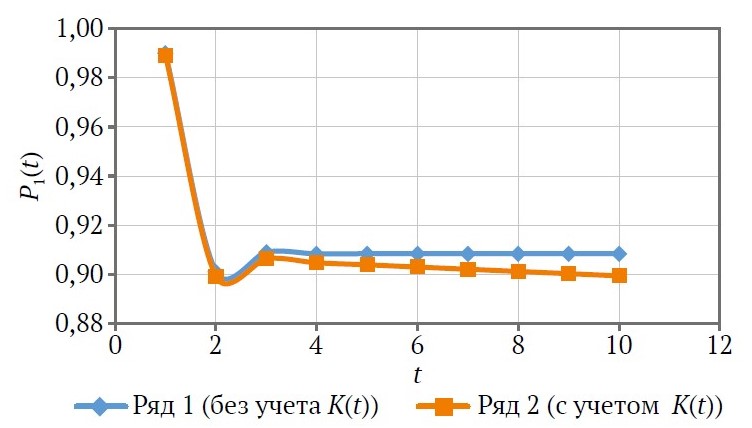
Рис. 2. Зависимость вероятности нахождения ВШЦ-16 в исправном состоянии от периода (сут)

Анализируя зависимость (рис. 2, ряд 2), видим, что вероятность нахождения системы в исправном состоянии снижается с увеличением периода эксплуатации и носит нелинейный характер. Таким образом, процесс качественного определения вероятности отказов сводится к уточнению стохастических коэффициентов.

Выводы

Использование модели однородных марковских процессов имеет свои границы, т. к. интенсивности переходов между отдельными состояниями системы далеко не всегда являются постоянными величинами, для случая зависящих от времени интенсивностей переходов расчеты становятся существенно сложнее. Кроме того, все или отдельные интенсивности переходов могут и вовсе не существовать. В этом случае невозможно составить систему дифференциальных уравнений с зависимыми от времени коэффициентами. Примерами таких динамических интенсивностей переходов могут служить в механических системах различные процессы старения.

Анализ эксплуатационной надежности вентилятора шахтного центробежного главного проветривания ВШЦ-16 показал, что вероятность безотказной работы этих агрегатов на Сибайском и Учалинском горно-обогатительных комбинатах хорошо согласуется по критерию Мизеса ω² = 2,38–3,64 и c экспоненциальным законом распределения ω² = 0,466–0,747∙10⁻⁴. Проверка независимости отказов вентиляторов «люфт рабочего колеса на валу» и «износ опорных подшипников», проведенный с помощью критерия независимости , не подтвердил гипотезу независимости этих отказов, так как вычисленный критерий t = 13,68 > 3,84 (табличного критерия). Таким образом, в рассматриваемом примере доказано, что отказы вентилятора шахтного центробежного главного проветривания ВШЦ-16 являются стохастически зависимыми событиями.

Для учета влияния отказов отдельных элементов на отказ всей системы процесс определения вероятности отказов может сводиться к уточнению стохастических коэффициентов. Подобный подход может стать новой основой для разработки методических принципов системы мониторинга и диагностики технического состояния вентиляционных систем. Кроме того, он может быть использован для создания методических принципов прогнозирования остаточного ресурса действующих вентиляторов на основе мониторинга их технического состояния.

В этом случае для анализа надежности привлекается аппарат теории конечных марковских цепей и полумарковских процессов. При наличии стохастической зависимости в потоках отказов механических систем применение теории марковских процессов возможно, но в этих случаях наилучшим инструментом для анализа надежности является численный метод статистических испытаний Монте-Карло [24].