Evaluation of variation of salt dust hygroscopic aerosol particle size as a function of relative air humidity

Introduction

The significant expansion of mineral extraction in current potash mines faced a problem of severe shortage of fresh air supply to a mine, which cannot be solved within the prevailing paradigm of autonomous independent ventilation of working areas. Under these conditions, almost all the prospects proved connected with sequential and (or) recirculation ventilation, as well as with the concept of "ventilation on demand", which require an adequate description of the processes of ventilation of mine workings, including the processes of "self-cleaning" of a mine air from dust at the levels of atoms, molecules, and clusters [1].

Crushing of a rock mass during mining operations in potash mines is inevitably accompanied by the formation of many aerosol hygroscopic salt particles of various sizes, which get into the air and form an aerodisperse medium. Instrumental measurements [2–4] show that in the process of mutual collision in humid air conditions salt particles aggregate and intensively precipitate on a drift floor. All this requires a detailed calculation of gas and dust conditions in a multi-connected network of mine workings of different aerodynamic types and process purpose on the basis of mathematical models adequate to reality, one of the obligatory members of which is the "runoff" of an impurity due to various kinds of micro-level interactions. One such interaction is the effect of relative humidity on the growth, consolidation, and coalescence of aerosols of the major potash mine rock minerals halite (NaCl) and sylvin (KCl). General regularities of such effect are known from phenomenological observations, but the details of these processes and their mathematical description required for digitalization of mine ventilation processes are missing [5, 6].

Moreover, the spectral size composition and dynamics of processes of interaction of salt aerosols with humid air have acquired independent significance in connection with the use of both underground spaces of rock-salt and potash mines for the purposes of so-called speleotherapy and ground sylvinite speleoclimatic chambers for speleoclimatotherapy [7].

The present paper is devoted to the consideration of the issues of mathematical description of the relative humidity effect on the size of hygroscopic aerosol particles.

The purpose of the research presented below is to determine the regularities of changes in the distribution (in size) of salt dust particles depending on the relative humidity of air, required for digitalization of mine ventilation to calculate and control the dust conditions in mine workings.

Achieving this goal required implementing the following measures:

• to review current ideas about the nature of a salt crystalline particle behavior at changing relative air humidity, its watering and efflorescence (recrystallization);
• to review the known physical models of hygroscopic particles growth, determine their applicability to the conditions of mine atmosphere;
• on the basis of known experimental and empirical data on hygroscopicity of salt-water aerosol particles to reveal and confirm the feasibility of their use in estimating the size change of hygroscopic salt dust aerosol particles in potash mines;
• on the basis of actual measurements in a field experiment in an air medium with salt aerosol to experimentally confirm the reliability of the results obtained on the basis of the proposed models of hygroscopic growth and the models of size distribution of salt aerosol particles in a mine atmosphere.

Techniques

The mineralogical and chemical composition of a salt aerosol depends on the corresponding parameters of salt rocks surrounding the airspace of a mine [5, 6]. The composition of salt rocks in potash mines is diverse and has been studied in detail for geological and mining-metallurgical purposes [8, 9]. The main practically important rocks are those formed by sodium chloride (halite), potassium chloride (sylvin) and potassium-magnesium chloride (carnallite) minerals: halite, sylvinite (red, banded, and mottled), carnallite. The interaction of relatively "moisture-resistant" halite and sylvin with air is especially important for mine operation [10], since carnallite, being a double aqueous salt of potassium and magnesium chlorides KCl×MgCl₂×6H₂O, contains itself molecular moisture and quickly "spreads" in humid air.

It should be noted that the interaction of NaCl (halite), KCl (sylvin) aerosol particles and host rock (sylvinite) with humid air remains insufficiently studied due to the relative slowness of natural processes of moisture condensation/evaporation and due to the extreme technical complexity of ensuring the operation of modern electronic measuring equipment [11] in conditions of aggressive and explosive environment. All this significantly complicates the quantitative study of the physics of salt aerosols in the conditions of underground mines and implementing appropriate field experiments, supplemented by the problems of financing such works.

In contrast to this situation, research on the impact of salt-water aerosol on the formation of the Earth's climatic conditions, the trends and consequences of the dangerous change of which are visible to all, due to its importance for the fate of mankind, receives the necessary relatively generous funding, despite the costliness of the experiments, which are increasingly being conducted with enviable persistence around the world.

Since salt-water aerosol is formed largely from NaCl and KCl particles, the results of salt-water aerosol studies (see, e.g., [12–14]) can and should certainly be taken into account as well-reliable instrumental studies for solving the problems discussed in this paper.

Findings

Current understanding of the mechanisms of deliquescence and efflorescence (recrystallization) of halite and sylvin aerosol particles

The most important role in the interfacial interaction of water vapor and salt particles is played by the essential fact that halite (NaCl) and sylvin (KCl) minerals have cubic syngony. Therefore, positively charged metal atoms, sodium Na⁺ and potassium K⁺ and negatively charged chlorine atoms Cl^– are structurally equivalent and form ionic structures of high stability: one sodium/potassium ion (Na⁺/K⁺) is surrounded by six chloride ions (Cl^–) and, conversely, one chloride ion is surrounded by six sodium/potassium ions. Thus a NaCl / KCl salt crystal of even a few nanometers in size retains its crystal properties (in dry air).

Salt aerosol particles have a strong affinity for water and, being hygroscopic, are enveloped by atmospheric moisture molecules, watered, dissolved, and grow due to the condensation of water vapor on a crystal [15], and the growth rate of particles with increasing relative air humidity naturally increases [16].

Four characteristic stages of transition from dry salt crystals to spherical drops of fully deliquesced salt solution can be distinguished in the mechanism of salt particle deliquescence when changing relative humidity RH, which is the result of hydrosorption processes at a "salt surface – humid air" contact.

At the first stage, characteristic of low RH values, the force fields of atoms on the surface of a dry salt crystal are only partially compensated by the force fields of neighboring atoms in the crystal lattice, and therefore they are able to interact with the force fields of atoms of water vapor molecules, always contained in an air. This interaction leads to the attraction of water molecules from the air to the solid surface and the formation of brine condensate, but due to the rather small number of water molecules in the air, the surface is not destroyed. In addition, at low water vapor elasticity, simultaneously with the attraction, water molecules previously deposited on the surface of salt crystals are released into the surrounding air. Thus, at RH of about 10–20%, the shape of the salt particles remains unchanged with preserving crystal surfaces corresponding to dry nonspherical crystalline particles [17].

At the second stage, the characteristic RH values are up to 70–75%. Under these conditions, a film of loosely bound water appears on the surface of salt particles in a relatively short period of time, which is highly aggressive towards easily soluble salts, and a salt mineral begins to deliquesce. The amount of water increases due to condensation [15], a crystal becomes more and more deliquesced, and finally water molecules envelop all surfaces of the deliquescing particle. The cubic shape of the particle with its sharp edges and corners disappears due to the fact that surface-adsorbed water deliquesces the salt crystal surface predominantly at the corners and edges of the crystals, where the field strengths attracting water molecules are stronger. Cubic particles become first near-cubic and then near-spherical [18], i.e., rounded (Fig. 1, a).

With further interaction with water vapor and increasing RH, a particle becomes large enough in size and tends to become an inhomogeneous sphere with a water shell (Fig. 1, b) [19], and, as for "large" particles, with a solid, partially nonspherical salt crystal core.

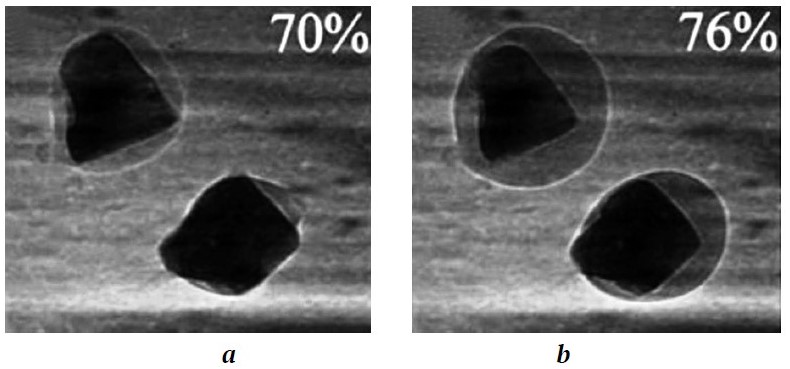
Fig. 1. Electron micrograph of sea salt crystal during deliquescence [15]: а – RH = 70%; b – RH = 76%

The third stage of the interaction between salt crystals and water in air leads to complete deliquescence (dissolution) of the crystals. If the RH exceeds a critical value called the salt deliquescence point due to atmospheric humidity or the deliquescence relative humidity DRH, the solid inner core of a particle, a salt crystal, deliquesces completely in a liquid drop and disappears, forming a homogeneous spherical drop of saturated solution [13].

The fourth stage is characterized by the fact that as RH increases above the DRH value, up to about 85–90%, the salt particles continue to increase at a slower deliquescence rate and become spherical droplets of solution at high RH values (e.g., about 99%) [17].

This is the above 4-stage process of moisture condensation on the surface of a salt aerosol particle until its complete deliquescence.

The reverse process, the release of moisture from the drops into the surrounding atmosphere and the efflorescence (recrystallization) of a salt, is so different from the deliquescence process that we can speak of hysteresis.

First, as RH decreases, a drop of unsaturated water-salt aerosol with a fully deliquesced salt crystal loses water along the same equilibrium vapor pressure curve, but remains in a liquid state and looks like a supersaturated brine drop, gradually decreasing in size due to water evaporation.

However, instead of "drying out" and efflorescence (crystallizing) at RH equal to DRH as one might expect, the salt aerosols remain hydrated and the solution remains supersaturated up to much lower RH values. This behavior is due to the fact that at a certain degree of "drying", to form a crystal, the hydrated Na⁺ and potassium K⁺ ions need to conjugate with Cl⁻ ions, and such atoms number should be enough for a crystal formation.

With a further decrease in relative humidity, having passed (after passing) the DRH value(s), a second critical relative humidity is reached, called an efflorescence point or Efflorescence Relative Humidity ERH, at which a salt particle begins to "solidify", gradually drying out and efflorescing (recrystallizing), now already representing a "solid-liquid" system [15, 20].

Since the DRH and ERH thresholds are different and relatively far apart in values, the presence of hysteresis leads to the fact that salt aerosol particles can exist in two forms, crystalline or aqueous, depending on the history (previous dynamics) of the RH change when the RH value is cycled. As a result, salt aerosol particles (both as solid, partially nonspherical salt crystals with a watery shell and as spherical droplets containing fully dissolved salt) can exist in the range of relative humidity values from about 45–50% to about 70–75%.It should be noted that for sylvinite as a rock composed of different minerals with different DRH and ERH thresholds, the deliquescence and efflorescence processes may be even more complex than described above. Meanwhile, since the ERH of most salts and salt mixtures is about 40%, in most cases observed under ordinary aqueous atmospheric conditions with characteristic RH values typically greater than 40%, the hysteresis in the curve of changing particle size due to the difference in relative humidities of deliquescence (DRH) and efflorescence (ERH) can be neglected.

Modeling the growth of hygroscopic salt particles

Many different physical models are now known that describe the growth of hygroscopic particles as a function of RH quite well.

To describe the changes of the dependence of the size (equivalent diameter) of a moistened aerosol particle D(RH) on RH, it is accepted to use a dimensionless value GF(RH), particle growth factor:

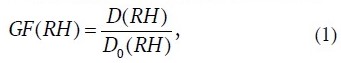where D₀(RH) is diameter of its dry base, a salt crystal at RH = 0%.

Note that, generally speaking, the growth factor at the same RH values depends on the absolute diameter of a dry particle that is especially evident for particles of a few tens of nm in size [11, 21, 22].

According to Koehler's k-theory [23], the hygroscopic properties of aerosol particles can be defined as a function of the hygroscopicity parameter k and water activity a_w in a drop of solution, defined as the ratio of the water vapor pressure over the flat surfaces of an aqueous salt solution to the vapor pressure over pure water at the same temperature. Under the condition of equilibrium of a salt aerosol droplet with water vapor and the nullity of the Kelvin effect describing the surface curvature that is true for particles of 100 nm and larger, a_w » RH/100, and Koehler's equation can be written as

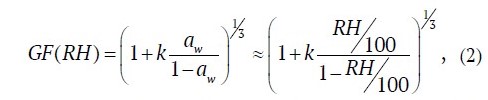
from where it is well seen that the larger k is, the greater the slope of the graph of GF = GF(a_w) » GF(RH/100) dependence is. The estimation for particles larger than 0.05 µm gives an error of substituting a_w for RH of no more than 5%, and, for particles larger than 0.1 µm, no more than 2%, which are quite acceptable for practical use.

Some of known literature data on hygroscopicity parameter k for salt aerosols are presented in Table 1.

Table 1

Salt aerosols hygroscopicity parameter k

For mixtures of soluble components, the hygroscopicity parameter can be approximated as the sum of its volume-weighted terms [23]:

where k_i is hygroscopicity parameter of an individual component of a mixture; ε_i is relative volume of a component in the mixture.

Our estimation of the range of the hygroscopicity parameter k variation for sylvinite gives the following: NaCl content in red sylvinite of the Kr-II formation of the Verkhnekamsk potassium-magnesium salt deposit varies within 71.51–73.20%, and that of KCl, 20.70–21.70%, while other components can be neglected. Then, taking into account the data of Table 1 for the salt aerosol (mixture of KCl and NaCl), characteristic of the air environment formed by potassium-magnesium salts, the hygroscopicity parameter varies in the range of 1.163 to 1.196, averaging 1.180.

A somewhat different (than (2)) model for describing the growth factor GF(RH) is presented in [16], according to which the model parameterization of GF(RH) is described by the following expression:

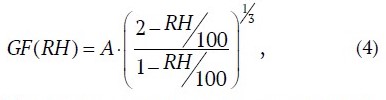
where A is parameterization factor, for salt-water aerosol equal to

A ≈ 1.081

according to [16].

The refinement of the dependence of the growth factor on water activity made in [27] to improve the approximation of experimental data suggests that the continuous hygroscopic growth of aerosol particles can be well described by the expression:

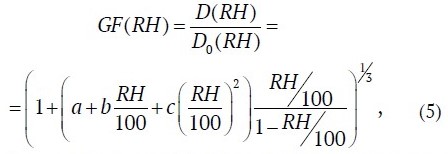
where a, b, c are approximation parameters depending on a particle species, presented in Table 2 for NaCl particles according to [27].

Table 2

Values of a, b, c parameters of model (5) (according to [27])

Models describing the GF(RH) dependence in the form presented below [28–30] have become widely used:

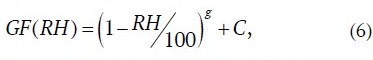
where g is so-called humidity factor; C is parameterization factor, the values of which for a number of salt aerosols are presented in Table 3.

Table 3

Values of g and C parameters in parameterization (6)

A summary of the various experimental data obtained by different researchers and authors is presented in Fig. 2. The solid line indicates the average value of the salt aerosol particle growth factor, characteristic of potash mines air, as a function of RH.

The obtained results were used in the study of the size of aerosol particles in a model air medium as a function of RH, which simultaneously allowed to verify the adequacy of the above theoretical views with respect to the specific conditions of salt aerosol in an air medium.

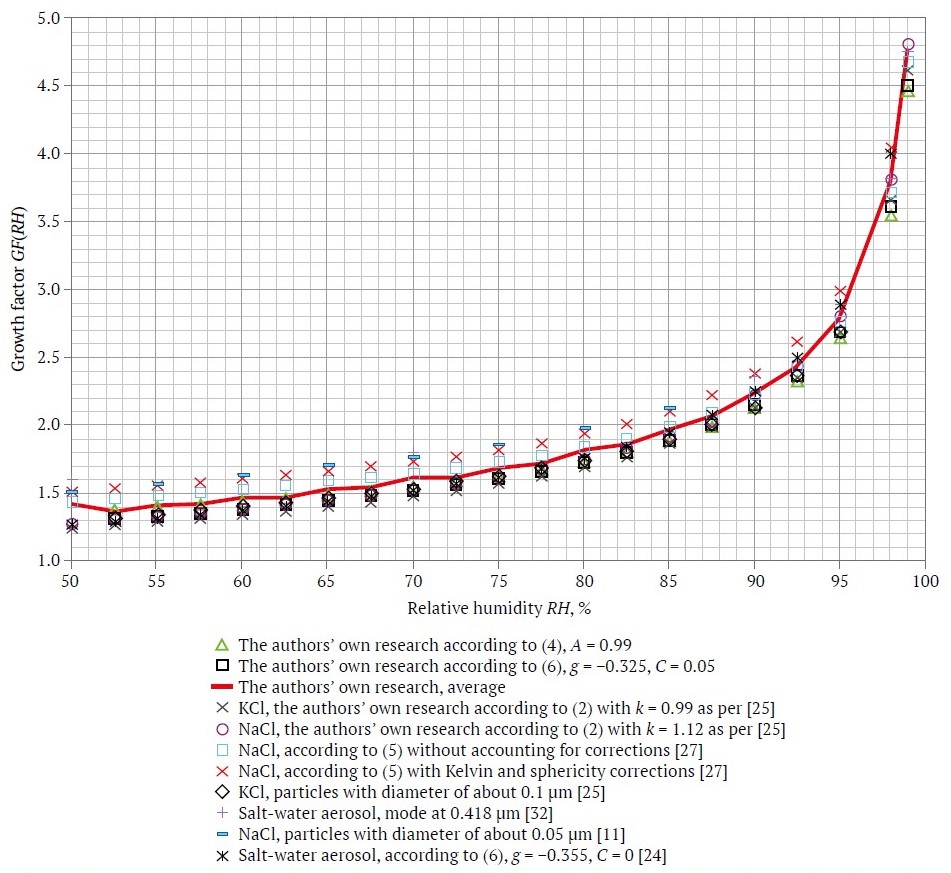
Fig. 2. Experimental and empirical data of growth factor of different salt aerosols depending on relative humidity

Experimental research

The authors selected a special model facility, a sylvinite chamber, which is an isolated room with the size of 2.0´3.5 m with controlled ventilation, all walls of which are lined with pressed salt sylvinite tiles 5–7 mm thick, manufactured by specialists of the Mining Institute of Perm Federal Research Center of the Ural RAS Branch, as a testing ground for experimental studies of the influence of relative air humidity on the counted size distribution of salt aerosol particles. The chamber ceiling 2.5 m high is ground halite, the floor is combined (passages are made of salt tiles cut from solid rock, and the rest of the area is coarsely crushed halite mixed with sylvinite).

The study of aerosol particle size distribution was carried out using an AZ-6 aerosol particle counter (PK.GTA-0.3-002), which allowed recording of aerosol particles of six size fractions: 0.3 µm and above, 0.4 µm and above, 0.5 µm and above, 0.6 µm and above, 0.8 µm and above, 1 µm and above. The measurement range of countable particle concentration was from 10² to 3×10⁵ dm^–3. The principle of the AZ-6 aerosol particle counter operation is optical and based on recording of scattered radiation. The tolerance limit of the basic relative error of aerosol counting concentration measurements in the range from 3×10⁴ to 2.5×10⁵ is ± 40%.

Relative humidity was recorded using an IVA-6A thermohygrometer, which allowed measuring temperature and relative humidity in the ranges from −20°C to +60°C and 0–98%, respectively. The tolerance limits of basic absolute error of relative humidity measurement at 23°С in the range of relative humidity of 0–90% is not more than 2%, and in the range of 90–98%, not more than 3%. The tolerance limit of absolute error of temperature measurement is not more than 0.1°C.

Long-term studies of the slowly changing microclimate were conducted while the RH value decreased from 90% (such maximum humidity was recorded in the chamber after several days of rainy weather) to 62% (after several consecutive sunny days).

The results of studies of aerosol particle size distributions (distribution density dN(D)/dD, where the differential dN(D) determines the number of particles in a unit volume, usually in one liter, dm⁻³, falling within a unit interval of diameter dD, usually in μm; bringing to one dimensionality, the aerosol particle distribution density dN(D)/dD are expressed in cm⁻⁴) in a model air medium, presented in Fig. 3, clearly show a decrease in aerosol particle concentrations with decreasing RH, especially for particles of about 0.3–0.5 μm in diameter. This is consistent with the mechanisms of salt particle watering and drying discussed above. While RH decreases, the particles gradually lose the water shell, decreasing in size, the mode of salt aerosol particle distribution shifts toward increasingly smaller particles, resulting in a decrease in the number of particles in the fixed particle size intervals of 0.3–1 μm.

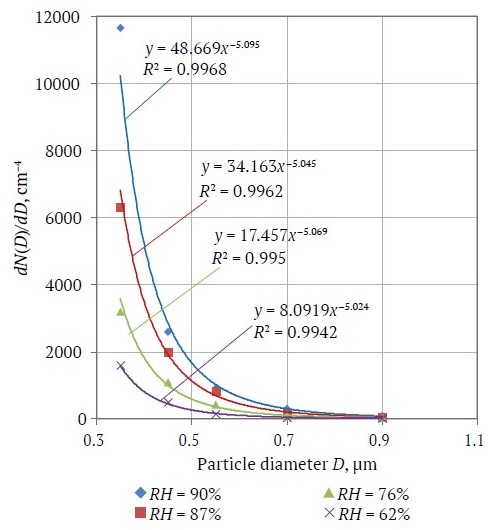
Fig. 3. Salt aerosol distributions by particle size at different relative humidity values

Findings Discussion

The approximation of the spectral size distributions of salt aerosol particles presented in Fig. 3 was carried out according to the well-known Young's model [33–35], cm⁻⁴:

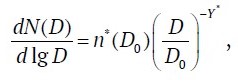
or

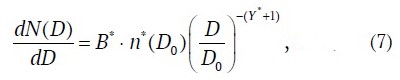
where dN(D)/d lgD is distribution density of counted particle concentration, cm^-3; N(D) is concentration of particles with diameter larger than D, cm⁻³; D₀ is arbitrarily chosen particle diameter in the range from about 0.1 μm to 10.0 μm, for which the validity of Young's model is reliably proved; ρ^*(D₀) is distribution density at D = D₀, cm^–3; Y^* is power exponent; B^* = 1/(ln 10) ≈ 0.434 is dimensional conversion factor, cm⁻¹.

This write−up of Young's model to describe the continuous size distribution of the counted concentration was selected for the reason that equation (7), operating with diameter ratios, allowed for comparability with the relationships for the growth factor GF(RH), also operating according to (1) with . In addition, equation (7) in log-log coordinates depicts the distribution function as a straight line.

The exponents of power in the functions approximating the power-series distributions of aerosol particles at different values of RH are not much different (see Fig. 3) and amount to Y^* = 4.06±0.03. This obtained value agrees well with historical results, according to which the values of the exponents of power in the Young's model for aerosols of different physical and chemical nature vary in the range Y^* = 2–5 [36].

The values of the distribution density ρ^*(D₀) in the approximating expressions presented in Fig. 3 decrease as RH decreases that also agrees with the previously presented reasoning about the salt aerosol particles efflorescence processes and with the regularities of the considered Young's model.

The regularities of the changes in the distribution density ρ^*(D₀) depending on RH can be obtained by taking the particle diameter as the diameter of a "dry" particle at RH = 0% and based on the averaged values of the hygroscopic growth factor obtained earlier and presented in Fig. 2. Fig. 4 shows the distributions of "dry" aerosol particles with diameter D₀ calculated from (7) together with (1), based on the values of GF(90%) = 2.13; GF(87%) = 1.97; GF(76%) = 1.65; GF(62%) = 1.44. According to Fig. 4 all distributions empirically recalculated to a "dry" residue for all considered cases of relative humidity were reduced in log-log coordinates to a single straight line and are described by the empirical expression

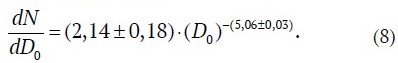
The obtained results allowed not only to confirm the reliability of the regularities of hygroscopic growth of sea salt particles known in atmospheric and ocean physics, but also to generalize the Young's size distribution (8) for the conditions of a mine atmosphere that allows using it in modeling dust conditions in mine workings of potash mines.

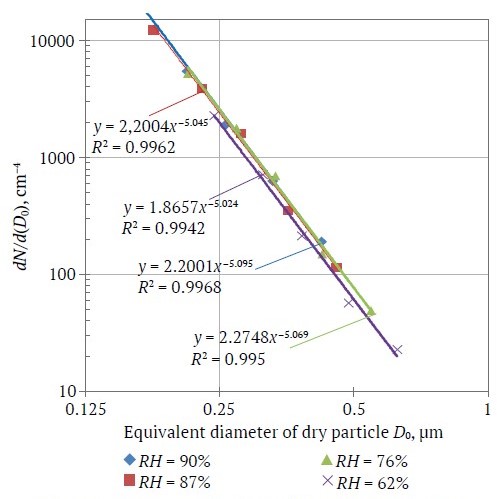
Fig. 4. Effective distribution of "dry" aerosol particles

Conclusion

The study demonstrated uniform regularities of hygroscopic growth of salt aerosol particle sizes as a function of relative air humidity, characteristic of both sea air and the air of potash mines.

The shown high convergence of the hygroscopic growth factor values (with mean value of root-mean-square deviation of 0.11 in the interval of the factor change of 1.26–4.77) borrowed from known models and known scientific data on watering and reverse efflorescence of salt particles of salt-water aerosol with the results obtained by the authors in a model air environment, typical for the atmosphere of a salt mine, confirms the feasibility of their use in modeling the processes of mine ventilation. The adapted for mine conditions expressions describing the size of hygroscopic aerosol particles consisting of halite (NaCl) and sylvin (KCl) crystals as a function of relative humidity allow building ventilation models adequate to actual conditions, required also in digitalization of potash mines ventilation.

The obtained averaged values of the growth factor for various conditions of particle watering and the confirmed reliability of application of Young's model with a power coefficient in the expression dN(D)/dD equal to −(5.06±0.03) can be used in the construction of mathematical models of salt dust behavior in mine workings and changing aerosol particle sizes at increasing and (or) decreasing relative air humidity that confirms their theoretical and practical significance for mine ventilation management.

Thus, the goals of the research presented in this paper have been achieved, and the set tasks have been solved in full.