Перейти к:
Определение модуля деформации и характеристик анизотропного поведения блочных массивов горных пород
https://doi.org/10.17073/2500-0632-2023-08-143
Аннотация
Всесторонне изучена анизотропия деформационного поведения блочных массивов горных пород. В качестве ключевого параметра выбран модуль одноосной деформации. В целом он является анизотропным и зависит от направления нагружения, а также от свойств ненарушенной породы, трещин и элементов их залегания. Представительные объемы блочных массивов горных пород были численно смоделированы методом дискретных элементов и одноосно нагружены в различных направлениях. Затем были изучены режим разрушения и модуль деформации для различных направлений нагружения и различных относительных элементов залегания трещин. Внедрена и использована новая нелинейная матрица жесткости трещин в зависимости от напряжения, в которой учитываются состояние поверхности трещин в виде коэффициента шероховатости (JRC) и ненарушенного массива пород в виде предела прочности при одноосном сжатии (UCS). Результаты оценок представлены в виде роз-диаграмм, демонстрирующих изменение модуля деформации блочного массива горных пород в зависимости от коэффициента шероховатости швов, прочности при одноосном сжатии ненарушенной породы и структуры массива горных пород по относительному углу трещины. Также представлена ожидаемая степень анизотропии для различных условий поверхностных трещин и прочности при одноосном сжатии ненарушенной породы. В таблице геологического индекса прочности (GSI) результаты классифицированы таким образом, что, присвоив значение JRC каждому классу состояния поверхности трещин, можно определить модуль деформации и степень анизотропии, соответствующие значениям GSI. Согласно этой схеме можно сделать вывод, что влияние шероховатости трещин на модуль деформации блочных массивов горных пород больше, чем влияние предела прочности при одноосном сжатии ненарушенной породы. Полученные результаты подтверждают идею о том, что блочный массив имеет критическую деформацию, которая не зависит от угла нагружения θ и направления третьей системы трещин α.
Ключевые слова
Для цитирования:
Ахрами O., Джавахери Купаи Х., Ахангари К. Определение модуля деформации и характеристик анизотропного поведения блочных массивов горных пород. Горные науки и технологии. 2024;9(2):116-133. https://doi.org/10.17073/2500-0632-2023-08-143
For citation:
Ahrami O., Javaheri Koupaei H., Ahangari K. Determination of deformation modulus and characterization of anisotropic behavior of blocky rock masses. Mining Science and Technology (Russia). 2024;9(2):116-133. https://doi.org/10.17073/2500-0632-2023-08-143
Определение модуля деформации и характеристик анизотропного поведения блочных массивов горных пород
Ключевые моменты
- Введены новые нелинейные зависимости от напряжения нормальной жесткости и жесткости на сдвиг трещин.
- Блочные массивы горных пород классифицируются по состоянию поверхности трещины и прочности нетронутой породы.
- Диапазоны модулей деформации и степень анизотропии классифицируются аналогично геологическому индексу прочности GSI.
- Степень анизотропии модуля деформации блочных массивов составила 1,6 ≤ RE ≤ 2,3 при среднем значении 1,88.
Символы уравнения
σn: нормальное напряжение;
σc: предел прочности при одноосном сжатии;
σci: предел прочности при одноосном сжатии ненарушенной породы;
σcm: предел прочности при одноосном сжатии массива горных пород;
τn: напряжение сдвига;
τf: пиковое напряжение сдвига;
τult: предельное напряжение сдвига;
φ: угол трения ненарушенной породы;
φj: угол трения трещины;
φb: базовый угол трения трещины;
a: эмпирическая постоянная;
C: сцепление ненарушенной породы;
Cj: сцепление трещины;
K: модуль объемной упругости ненарушенной породы;
G: модуль сдвига ненарушенной породы;
T: прочность на разрыв ненарушенной породы;
Tj: прочность на разрыв трещины;
Ei: модуль упругости ненарушенной породы;
Em: модуль деформации массива горных пород;
Emax: максимальный модуль деформации массива горных пород;
Emin: минимальный модуль деформации массива горных пород;
GSI: геологический показатель прочности;
JRC: коэффициент шероховатости трещины;
JCS: прочность на сжатие стенки трещины;
UCS: предел прочности при одноосном сжатии;
Kn: нормальная жесткость трещины;
Ks: жесткость сдвига трещины;
Ksn: эффекты сопряжения между напряжением сдвига и нормальным поведением трещины;
Kns: эффекты сопряжения между напряжением сдвига и нормальным поведением трещины;
Kni: исходная нормальная жесткость трещины;
Ksi: исходная жесткость сдвига трещины;
Rf: коэффициент разрушения;
RE: степень деформационной анизотропии;
Un: нормальное относительное смещение трещины;
Us: относительное смещение трещины скалывания;
Unc: максимальное вертикальное смещение трещины;
U: раскрытие трещины в начале нагружения;
UsPeak: смещение при сдвиге при пиковой прочности;
D: коэффициент разрушения массива.
Введение
Модуль деформации массива горных пород является одним из основных параметров геомеханики тоннелей, горных выработок и других геотехнических сооружений, возводимых в горных породах. Механические свойства массива горных пород как трещиноватой среды определяются ненарушенной породой, относительной схемой размещения системы трещин, геометрическими параметрами трещин, а также их механическими свойствами. Механические свойства, определяемые системами трещин как плоскими нарушениями сплошности, зависят от их масштаба и направления. Каждая система трещин накладывает анизотропию в направлении своего нормального вектора. Если массив горной породы сильно раздроблен, можно предположить, что анизотропия, налагаемая отдельными трещинами в любом направлении, распределена равномерно, поэтому массив горной породы изотропен. В противном случае, даже при размерах, превышающих представительный элементарный объем (REV), в котором массив горных пород можно рассматривать как континуум, его зависимость от направления трещин не исчезнет.
Для массивов горных пород с простой трещиноватостью для оценки модуля деформации можно использовать некоторые аналитические зависимости, например [1–4]. Другим примером такого типа зависимостей является трехмерная эквивалентная непрерывная модель, которую Кулави (Kulhawy) [5] представил для массива горных пород с тремя системами ортогональных трещин, проявляющего ортотропное поведение. Однако найти решение в замкнутой форме для модуля деформации массива с многочисленными системами трещин или при использовании более продвинутых определяющих свойств для ненарушенной породы и трещин невозможно. Следует отметить, что эмпирические методы, которые обычно применяются в механике горных пород для оценки деформируемости массива, например, представленные в [6–8], игнорируют влияние анизотропии массива. Также отсутствует математическая платформа для создания поведенческой модели.
Поскольку механические свойства массива горных пород полностью зависят от масштаба, в экспериментальных методах размеры проб горных пород и измерительных датчиков редко соответствуют реальному массиву или пропорциональны ему. Хойз (Heuze) [9] пришел к выводу, что модуль деформации массива горных пород, измеренный в полевых условиях, лежит в широком диапазоне от 20 до 60 % от модуля деформации ненарушенной породы, измеренного в лаборатории. Полевые испытания дорогостоящие, требуют много времени и сложно интерпретируются из-за наличия неопределенных трещин, неопределенных граничных условий и зачастую используются с осторожностью в качестве представительных для масштаба нарушенного массива горных пород. Кроме того, для характеристики существенной анизотропии массива горных пород необходимо провести несколько испытаний в различных направлениях.
Численное моделирование массивов горных пород как трещиноватых невыдержанных сред обычно реализует две общие методики. Одна из них – метод континуума, в котором роль нарушений сплошности неявно учитывается с помощью эквивалентных механических свойств [1, 10]. Другой метод заключается в применении численных методов решения, таких как методы дискретных элементов, конечных элементов или конечных разностей, в которых нарушения сплошности могут быть смоделированы в явном виде. Метод дискретных элементов был принят широко, поскольку он дает преимущество при описании геометрических параметров и определяющих соотношений трещин и ненарушенной породы. Метод дискретных элементов был введен Кандаллом (Cundall) [11] и затем развит другими исследователями [12, 13]. Многие исследования механического поведения массивов горных пород были реализованы с использованием метода дискретных элементов [14–16].
В данном исследовании рассматривается модуль анизотропной деформации блочных массивов горных пород, образованных тремя системами трещин, – двумя ортогональными, секущимися третьей. Работы выполнялись путем дискретно-элементного моделирования представительных объемов блочных массивов.
Наиболее важным фактором, влияющим на деформационное поведение массива, является жесткость его трещин и нарушений сплошности. Выражая жесткость плоских нарушений сплошности через нормальную Kn и сдвиговую Ks составляющие, становится очевидно, что определение этих составляющих является одним из важнейших моментов в оценке жесткости массива горных пород. Чем ближе их определение к реальным условиям, тем выше точность определения модуля деформации массива. Таким образом, для расчета модуля деформации массива горных пород необходимы эффективные зависимости, которые могут точно выразить нелинейное поведение трещин. Для решения этой проблемы была внедрена и использована для моделирования новая нелинейная матрица жесткости для трещин в зависимости от напряжения. Она учитывает реальное нелинейное поведение трещин через их основные параметры без необходимости проведения многочисленных испытаний. Насколько нам известно, данное исследование является единственным, которое напрямую учитывает основные параметры трещин при расчете модуля массива, что делает точность и применимость результатов уникальными.
Цель данного исследования – представить реалистичное анизотропное поведение блочных массивов горных пород путем сочетания численного моделирования и математико-эмпирической зависимости для жесткости трещин в практически применимом виде. Полученные результаты касаются модуля деформации, механизма разрушения и поведения после разрушения для различных направлений нагружения, а также степени анизотропии в обобщенном виде. Модули деформации представлены в виде роз-диаграмм, которые показывают изменение модуля деформации блочного массива горных пород в различных направлениях в зависимости от исключительно присущих массиву параметров. Такими параметрами являются параметры трещин в виде коэффициента шероховатости (JRC), ненарушенного массива пород в виде предела прочности при одноосном сжатии (UCS), а также структура массива с точки зрения относительного угла ориентации трещины. Данные диаграммы позволяют оценить модуль деформации блочного массива в различных направлениях без проведения лабораторных и полевых испытаний или эмпирических соотношений. Кроме того, в таблице геологического индекса прочности (GSI) результаты классифицированы таким образом, что, присвоив значение JRC каждому классу состояний поверхности трещин, можно определить модуль деформации и степень анизотропии, соответствующие значениям GSI.
1. Стратегия моделирования
Для изучения состояния анизотропии в блочных массивах горных пород методом дискретных элементов (с помощью ПО 3DEC, Itasca 20131) были смоделированы представительные объемы массивов горных пород, которые нагружались одноосно в различных направлениях.
Затем для различных относительных параметров трещин (различных блочных массивов) определялись режим разрушения и модуль деформации для различных направлений нагружения. Процедура моделирования включала в себя: а) определение геометрических параметров блочных массивов горных пород; б) приложение одноосной нагрузки в различных направлениях к выбранному массиву; в) параметрическое определение механического поведения трещин и ненарушенной породы; г) определение представительного объема массивов горных пород. Эти вопросы рассматриваются ниже.
1Itasca Consulting Group Inc., 2013. 3DEC 5.00, User’s Guide, Itasca Consulting Group, Inc.
1.1. Геометрические параметры исследуемых глыбовых массивов горных пород
Термин «блочный массив» обычно применяется к массиву горных пород с тремя системами трещин [17]. В данном исследовании рассматриваются блочные массивы, включающие две ортогональные системы трещин, секущиеся третьей, как показано на рис. 1. На рис. 1 система трещин 3 образует угол α со второй системой трещин, а ее простирание нормально к простиранию первой системы трещин. В настоящем исследовании были рассмотрены различные массивы со значениями угла α 5°, 15°, 30°, 45°, 60°, 75° и 90°.
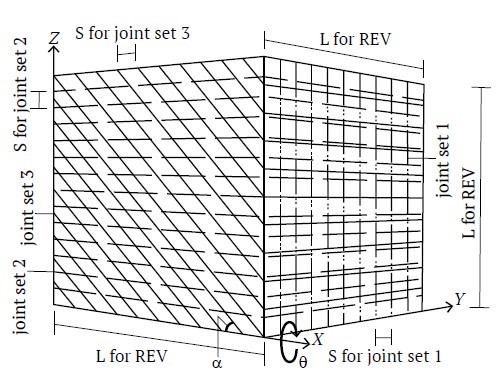
Рис. 1. Блочный массив с двумя ортогональными системами трещин, секущимися третьей под углом α: Joint set – система трещин; for REV – для представительного элементарного объема
1.2. Схема нагружения
Для оценки анизотропного поведения моделей элемент с представительным объемом массива нагружался одноосно в разных направлениях. Это нагружение нормально к плоскости с простиранием, параллельным оси X, а его направление отклоняется от оси Z на угол θ.
На рис. 2 показаны направления одноосных нагружений блочного массива с углом α = 45º. В качестве другого примера на рис. 3, а показана модель блочного массива с α = 90° и θ = 0, а на рис. 3, б – модель блочного массива с α = 90° и θ = 45º.
Модели 3DEC выполнены в виде кубов с осями, параллельными глобальной программной среде, при этом одноосная нагрузка всегда прикладывается в направлении глобальной вертикальной оси. Для каждой системы трещин для нагружения массива с углом θ плоскости трещин поворачивались вокруг глобальной оси x на угол θ, как показано на рис. 1.
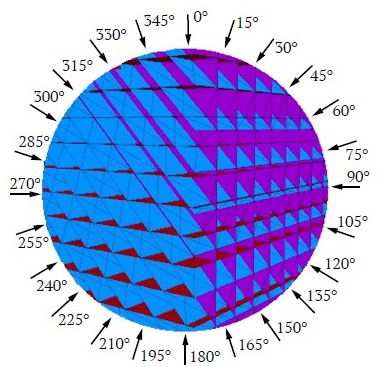
Рис. 2. Направления одноосных нагружений блочного массива с углом α = 45°
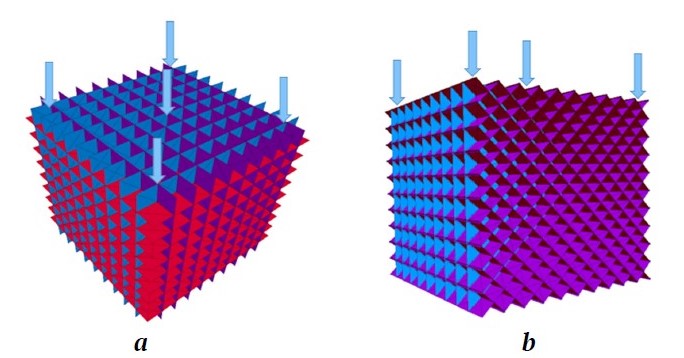
Рис. 3. Блочный массив с: а – α = 90°, нагруженный на θ = 0; б – α = 90°, нагруженный на θ = 45°
1.3. Механические свойства трещин
Общее определяющее выражение для деформации трещин может быть записано в виде:
где σn – нормальное напряжение; τn – напряжение сдвига; Un – нормальное относительное смещение; Us – сдвиговое относительное смещение трещины; Kn и Ks – нормальная жесткость и жесткости сдвига трещины соответственно; Ksn и Kns – коэффициенты сопряжения сдвигового и нормального поведения трещины, которыми в данном исследовании пренебрегли. Для того чтобы учесть реалистичное поведение жесткости трещин в моделях, ниже вводятся новые нелинейные выражения, зависящие от напряжения, для диагональных компонентов матрицы жесткости трещин. Эти выражения определяют компоненты матрицы жесткости в зависимости от нормального напряжения к трещине σn состояния поверхности трещины с точки зрения коэффициента шероховатости трещины (JRC) и материала ненарушенной породы с точки зрения предела прочности при одноосном сжатии ненарушенной породы σci.
1.3.1. Нормальная жесткость
Нормальное поведение трещины может быть описано гиперболической моделью, предложенной в [18, 19], как:
где Un – вертикальное смещение по трещине; Unc – максимальное вертикальное смещение по трещине; a – эмпирическая постоянная. На рис. 4 показано типичное нормальное поведение трещин. Из определения Kn и уравнения (2):
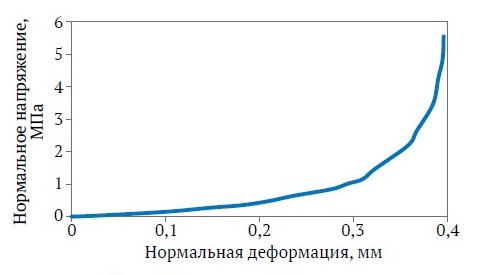
Рис. 4. Типичное нормальное напряженно-деформационное поведение трещин
Таким образом, начальная нормальная жесткость трещины Kni в начале нагружения при Un = 0 составляет:
Решив уравнение (4) для a с точки зрения Unc и Kni и уравнение (2) для Unc и подставив их в уравнение (3), получим:
Уравнение (5) выражает нормальную жесткость трещины в заданном состоянии напряжения и деформации по отношению к его начальному значению Kni , которое можно оценить следующим образом.
Бандис и др. (Bandis et al.) [19] предложили представить исходную нормальную жесткость трещин как:
Kni = −7.15 + 1.75JRC + 0.02 [JCS/U], (6)
где JRC – коэффициент шероховатости поверхности трещины; JCS – прочность стенки трещины на сжатие, МПа, которая может быть равна прочности на сжатие ненарушенной породы σci; U – раскрытие трещины в начале нагружения, мм. U может быть оценено как [19]:
U = JRC [0.04σci/JCS − 0.02]. (7)
Подставив U из уравнения (7) в уравнение (6), получим выражение для оценки Kni.
1.3.2. Жесткость при сдвиге
Зависимость между относительным смещением при сдвиге Us и напряжением сдвига τ может быть выражена гиперболической функцией [19–21] следующим образом:
τ = [1/(KsiUs) + Rf/τf]−1, (8)
где Ksi – начальная жесткость при сдвиге; τf – прочность при сдвиге трещины; Rf – коэффициент разрушения (τf /τult); τult – предельное напряжение сдвига.
Таким образом:
Ks = (dτ)/(dUs) = Ksi [1+(RfKsiUs)/τf]−2, (9)
Us = [Ksi/τ −(RfKsi)/τf ]−1. (10)
При прочности при сдвиге трещины, используя τ = τf и Us = Uspeak из уравнения (10), получим:
Согласно [22] смещение при сдвиге при пиковой прочности вдоль трещины можно считать равным 0,01 длины трещины или тектонического блока; таким образом, относительное смещение при сдвиге Uspeak составляет 0,01 и согласно уравнению (11):
Подставив уравнения (10) и (12) в уравнение (9), получим:
Согласно [19]:
Ksi = (−17.19 + 3.86JRC)(σn)0.783. (14)
и следующему [23–25]:
1.4. Механические свойства ненарушенной породы
Предполагалось, что ненарушенная порода ведет себя как изотропный упруго-идеально пластичный материал, а в качестве модели текучести или разрушения были приняты критерии Мора–Кулона. Связь между модулем упругости Ei и прочностью при одноосном сжатии σci ненарушенной породы выбрана из зависимостей, предложенных в [26]. Они предложили следующие зависимости между σci и числом отскока молотка Шмидта Rn(l), а также между Ei и Rn(l):
Ei = 0.6005ρRn(l) − 2.0276, GPa, (17)
что дает следующие результаты:
Ei = 69.023 log(0.145σci) − 13.07, GPa, (18)
где σci дано в МПа. Уравнения (16) и (17) были предложены на основе экспериментальных результатов по 28 литологиям и 3 типам пород [26].
Коэффициент Пуассона выбран равным 0,25.
Сцепление ненарушенной породы C выбрано как [27]:
C = 0.16σci. (19)
Для угла трения ненарушенной породы выбирается представительное для каждой группы значение отклонения σci, представленное в табл. 1, на основе типичных значений φ для различных типов по род [22, 28].
Таблица 1
Выбранная корреляция между прочностью при одноосном сжатии и углом трения ненарушенной породы
| σci, МПа | φ, град |
| σci < 50 | 25 |
| 50 < σci < 100 | 30 |
| 100 < σci < 250 | 35 |
1.5. Представительный элементарный объем массива горных пород
Известно, что в массивах горных пород с систематическим расположением трещин механическое поведение зависит от масштаба. В зависимости от относительного размера блока (отношение размера блока к характерному размеру массива, например, S/L на рис. 1) поведение массива горных пород может варьироваться от поведения ненарушенной породы до асимптотического значения в большом масштабе, при котором массив может рассматриваться как континуум. Куба (Cuba) [29] предположил, что в качестве «представительного элементарного объема» (REV) может быть выбран определенный масштаб, выше которого характеристики домена остаются в основном постоянными. Для оценки этого масштаба могут быть использованы эмпирические зависимости. Шульц (Schultz) [30] предложил масштаб, превышающий размер блока или расстояние между трещинами в 5–10 раз (относительный размер блока равен 0,2–0,1).
Для кубического объема, содержащего три системы трещин с равномерным расстоянием между трещинами S и размером L, минимальный относительный размер L/S представительного элементарного объема может быть определен путем последовательного анализа одноосного поведения куба. Выбранный объем имеет две ортогональные системы трещин, секущиеся третьей системой с α = 45° (см. рис. 1). Результаты для пиковой прочности при одноосном сжатии и одноосной секущей жесткости, соответствующей 50 % пиковой прочности E50, представлены на рис. 5. На этом рисунке в качестве масштаба REV выбрано значение L/S = 10.
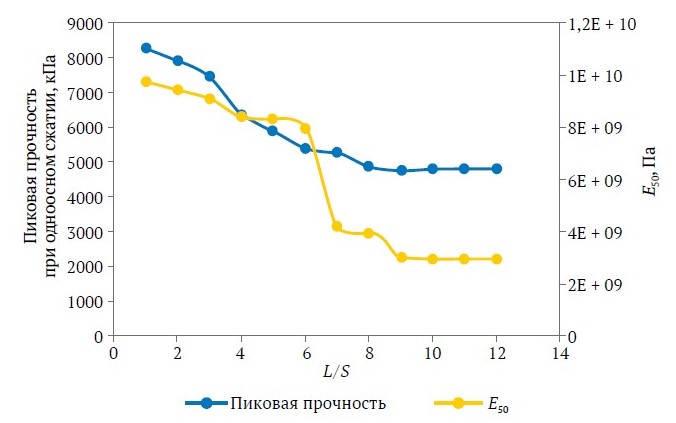
Рис. 5. Изменение пиковой прочности при одноосном сжатии и E50 блочного массива горных пород (α = 45° на рис. 1) при L/S (модуль сдвига ненарушенной породы G = 4 ГПа; модуль объемного сжатия ненарушенной породы K = 6,66 ГПа; ϕ = 25, v = 0,25, c = 2,4 МПа)
2. Подтверждение стратегии моделирования
Подтверждение реализованной процедуры было выполнено путем ряда сравнений существующих результатов и прогнозов численного моделирования. Сюда входит сравнение: а) моделируемого изменения прочности при одноосном сжатии UCS массива горных пород с одной системой трещин с результатами решения в замкнутой форме (разд. 2.1); б) прогнозируемого режима разрушения массивов горных пород с результатами экспериментального моделирования (разд. 2.2); в) прогнозируемого модуля анизотропии горной породы с одной системой трещин с результатами экспериментального моделирования (разд. 2.3).
2.1. Моделирование UCS массива горных пород с одной системой трещин
Джегер предложил для прогнозирования изменения прочности при одноосном сжатии массива с одной системой трещин для различных направлений использовать решение в замкнутой форме [31]. На рис. 6 приведено сравнение UCS численной модели цилиндрического образца с одной системой трещин с решением, предложенным в [31]. Угол наклона трещин к вертикальной оси варьируется от 0 до 90°. В численном решении цилиндрическая породная проба диаметром 2 м и длиной 4 м была нагружена до разрушения. На рис. 6 приводится сравнение значений UCS. Как видно из рис. 6, результаты в основном соответствуют решению Джегера и др. (Jaeger et al.) [31]. Характеристики ненарушенной породы и трещин приведены в подписи к рис. 6.
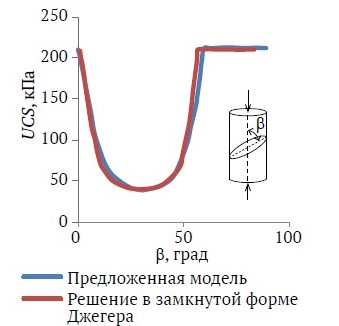
Рис. 6. Отклонение UCS массива горных пород с одной системой трещин с обозначением угла падения трещин: параметры ненарушенной породы: G = 4,28 ГПа; K = 1,75 ГПа; φ = 40; T = 200 кПа; параметры трещин: cj = 10 кПа; φj = 30; Tj = 20 кПа; Kn = 15 ГПа/м; Ks = 12 ГПа/м
2.2. Моделирование экспериментов по изучению режимов разрушения трещиноватых пород
Янг и др. (Yang et al.) [32] провели серию испытаний физических моделей с целью изучения режима разрушения и анизотропии трещиноватых пород. Эти модели включали смоделированные пробы горных пород (из цемента и песка) с одной или двумя неортогональными системами трещин, как представлено в табл. 2. В табл. 2 также приведено сравнение состояний разрушения по результатам испытаний по данным [32] с результатами численного моделирования этих моделей, которые совпадают.
Таблица 2
Сравнение видов отказов в физических и численных моделях
| Предлагаемая модель | Результат испытания | Массив с одной системой трещин |
Падение = 0 Падение = 90 | Разрушение ненарушенной породы Разрушение ненарушенной породы | Intact rock failure Intact rock failure |
| Предлагаемая модель | Результат испытания | Массив с двумя системами трещин |
Падение = 0/90 Падение = 60/−60 (60/120) Падение = 40/−40 (40/140) | Разрушение ненарушенной породы Скольжение по трещине Смешанное разрушение (скольжение по трещине + ненарушенная порода) | Разрушение ненарушенной породы Скольжение по трещине Смешанное разрушение |
2.3. Моделирование экспериментов по определению модуля деформации трещиноватых пород
На рис. 7 показано сравнение экспериментального модуля деформации, полученного в [32], с результатами численного моделирования массива горных пород с одной системой трещин. Согласованность между экспериментальными результатами и результатами численного моделирования очевидна.
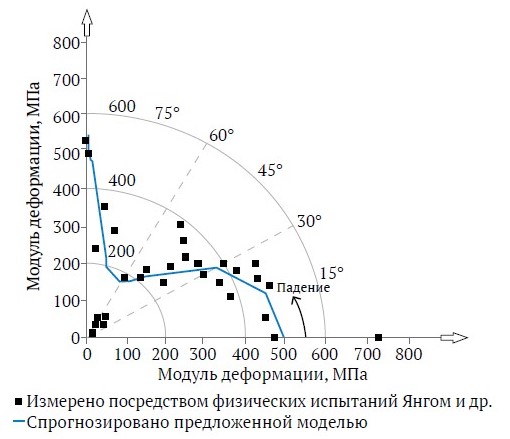
Рис. 7. Сравнение экспериментального модуля деформации, полученного в [32], с результатами численного моделирования массива горных пород с одной системой трещин. Фундаментальные свойства материала модели: G = 1,913 ГПа; K = 2,448 ГПа; JCS = 7,63 МПа; φ = 31; σt = 1,05 МПа; v = 0.19; уд. вес = 1,05 г/см3; σc = 7,63 МПа
3. Результаты моделирования
3.1. Анизотропия в напряженно-деформационном поведении массива и механизм разрушения
При одноосном нагружении массива горных пород возможными механизмами разрушения являются разрушение ненарушенной породы, разрушение в результате скольжения по трещинам и сочетание этих двух режимов. В ходе анализа были изучены кривые напряжения и деформации и режимы разрушения. Механизмы разрушения и поведение после разрушения для каждого направления нагружения представлены в табл. 3 и 4.
Таблица 3
Механизмы разрушения блочных массивов (см. рис. 1)
| θ | α | ||||||
| 5 | 15 | 30 | 45 | 60 | 75 | 90 | |
| 0° | IRF + JS | IRF + JS | IRF + JS | JS | JS | IRF + JS | IRF |
| 15° | IRF + JS | IRF + JS | JS | JS | IRF + JS | IRF + JS | IRF + JS |
| 30° | JS | JS | JS | JS | JS | JS | JS |
| 45° | JS | JS | JS | JS | JS | JS | JS |
| 60° | JS | JS | JS | JS | JS | JS | JS |
| 75° | IRF + JS | IRF + JS | JS | JS | JS | IRF + JS | IRF + JS |
| 90° | IRF + JS | IRF + JS | IRF + JS | JS | JS | IRF + JS | IRF |
Примечание: IRF – разрушение ненарушенной породы; JS – скольжение по трещине
Таблица 4
Поведение после разрушения блочных массивов на рис. 1
| θ | α | ||||||
| 5 | 15 | 30 | 45 | 60 | 75 | 90 | |
| 0° | P & B | P & B | S & B | P & S | P & S | P & B | P & B |
| 15° | P & B | P & S | S | S | S & B | S & B | S & B |
| 30° | P & S | S | S | S | P & S | P & S | S |
| 45° | P & S | S | S | S | S | S | P & S |
| 60° | P & S | S | P & S | S | S | S | S |
| 75° | P & B | P & B | S | S | S | P & B | P & B |
| 90° | P & B | P & B | S & B | P & S | S & B | P & B | P & B |
Примечание: P – совершенно пластичное; S – разупрочненное; B – хрупкое
Так, в случае сильно нарушенных пород (0 < JRC < 4 и σci < 25 МПа) при выборе σci = 15 и JRC = 2 в качестве средних значений кривые осевого напряжения–деформации изменяются в зависимости от направления относительного одноосного нагружения (рис. 8); σci – прочность при одноосном сжатии ненарушенной породы. Для каждой кривой на рисунке также указан режим разрушения.
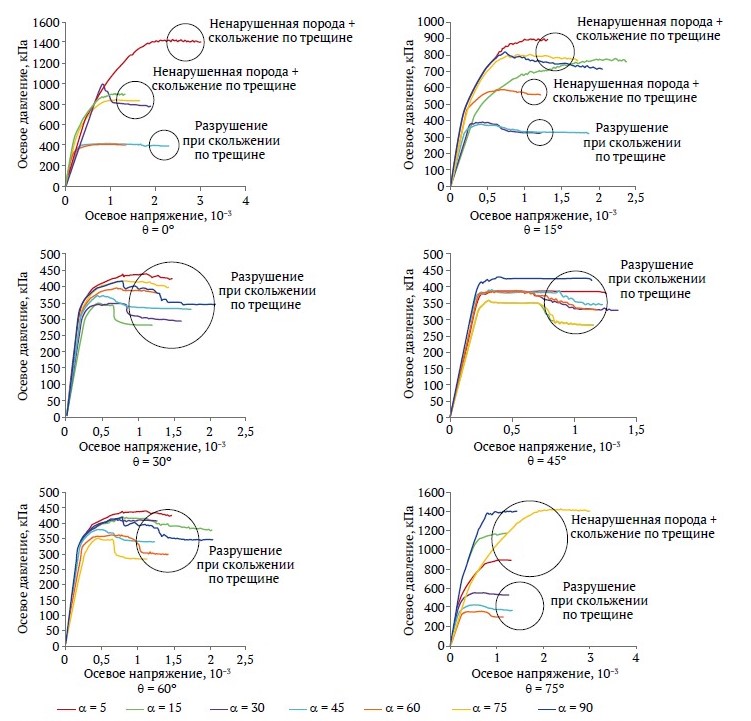
Рис. 8. Сравнение кривых напряжения-деформации для различных направлений третьей системы трещин α при различных углах нагружения θ для нарушенного блочного массива (JRC = 2 и σci = 15 МПа)
Если направление нагружения нормально или параллельно каждой из трещин (θ = 0 или θ = 90) и (α = 0 или α = 90), разрушение блочного массива горных пород произошло из-за разрушения в материале породы. В других случаях разрушение массива происходило как скольжение по трещинам или как сочетание скольжения по трещинам и разрушения ненарушенной породы. При изменении направления нагружения от 15 до 75° (15 ≤ θ ≤75) разрушение в блочном массиве горных пород происходило как скольжение по трещинам. В этом случае прочность при одноосном сжатии массива σcm составляет 0,35–0,45 МПа (σcm < 0,03σci). Если θ варьирует от 0 до 15° или от 75 до 90° (0 < θ < 15 или 75 < θ < 90), разрушение происходит как сочетание разрушения ненарушенной породы и скольжения по трещинам. В этом случае σcm изменяется от 0,8 до 1,4 МПа (σcm < 0,1σci). Для относительно ненарушенного блочного массива (4 < JRC < 8 и 50 < σci <100), если разрушение происходит как скольжение по трещинам, σcm < 0,05σci; если же разрушение происходит как сочетание разрушения неповрежденной породы и скольжения по трещинам, то σcm < 0,16σci. Для ненарушенного блочного массива (8 < JRC < 12 и 100 < σci < 250), если разрушение происходит как скольжение по трещинам, σcm < 0,14σci, если же разрушение происходит как сочетание разрушения неповрежденной породы и скольжения по трещинам, то σcm < 0,4σci. На рис. 9 для краткости показана часть этих результатов.
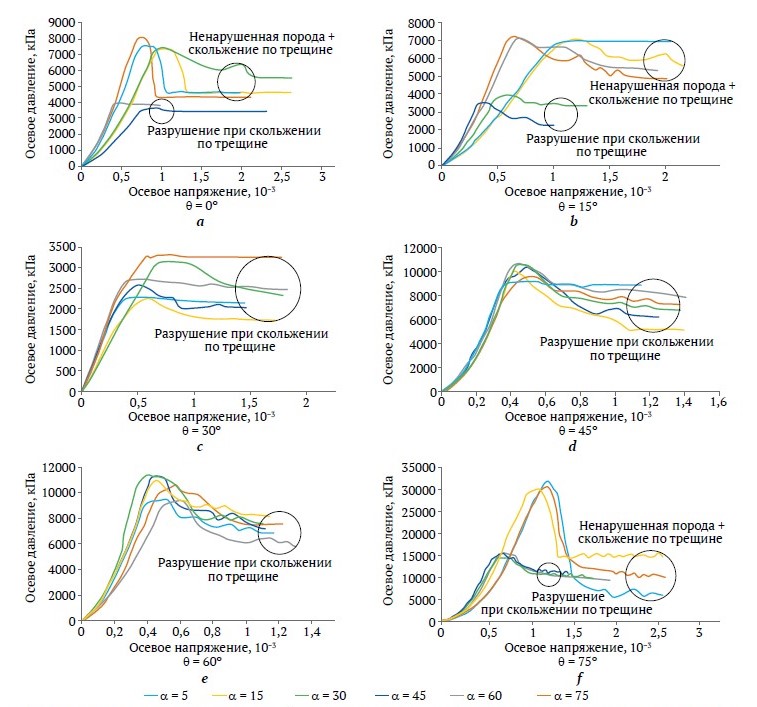
Рис. 9. Сравнение кривых напряжения-деформации для различных направлений третьей системы трещин α при различных углах нагружения θ: a, b, c – для относительно ненарушенного блочного массива (JRC = 8 и σci = 80 МПа); d, e, f – для ненарушенного блочного массива (JRC = 12 и σci =150 МПа)
Стоит отметить, что, если разрушение в блочном массиве происходит посредством скольжения по трещинам при θ = 30, θ = 45 и θ = 60, деформация текучести составляет от 0,2 до 0,4 и не зависит от угла нагружения θ и направления третьей системы трещин α. При разуплотнении образцов после пикового напряжения наблюдаются явления поворота блока в массиве и зигзагообразный рисунок поверхности разрушения.
3.2. Анизотропия в модуле деформации блочных массивов
Поскольку предполагается, что модуль деформации зависит от свойств трещин и ненарушенной породы, а также направления, блочные массивы пород были классифицированы по состоянию трещин по JRC как 0 < JRC < 4, 4 < JRC < 8, 8 < JRC < 12, 12 < JRC < 16, 16 < JRC < 20 и по UCS ненарушенной породы как σci < 25, 25 < σci < 50, 50 < σci < 100, 100 < σci < 250 МПа. Модуль деформации каждой группы рассчитан для различных направлений α. Результаты расчетов представлены в полярной системе координат, приведенной на рис. 10.
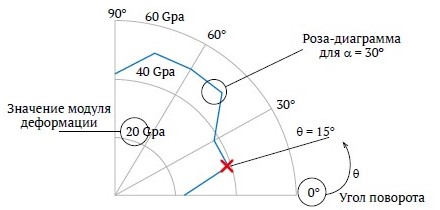
Рис. 10. Полярная система координат для представления модуля деформации блочного массива в зависимости от θ (кривая на графике приведена для 16 < JRC < 20, 50 < σci < 100 МПа и α = 30°)
В этой системе угол θ (определенный на рис. 1) находится в положительном тригонометрическом направлении от 0 до 90°, а значение модуля деформации измеряется в радиальном направлении от
центра. На этих рисунках модуль деформации указан в ГПа. На рис. 10 кривая на графике приведена для 16 < JRC < 20, 50 < σci <100 МПа и α = 30°. Каждая точка на этой кривой, которая приписывает значение E значению θ с шагом в 5°, рассчитывается следующим образом:
- для конкретного значения θ;
- для σci от 50 до 100 МПа на 5 шагов (60, 70, 80, 90, 100 МПа);
- для JRC от 16 до 20 на 4 шага (17, 18, 19, 20);
- для каждой пары JRC и σci рассчитывается E, а их среднее значение приписывается значению θ.
Результаты приведены на рис. 11–14. На этих рисунках каждая кривая соответствует определенному значению α. Согласно рисункам, зная структуру массива α, условия залегания трещин (на основе JRC) и материалы ненарушенных пород (представленные σci), можно получить модуль деформации массива из кривых для различных направлений нагружения. Так, на рис. 10 для массива горных пород с двумя ортогональными системами трещин и третьей системой трещин с α = 30, если состояние трещины очень хорошее (16 < JRC < 20) и 50 < σci < 100 MПa, для θ = 15° значение модуля деформации составит 39 ГПа.
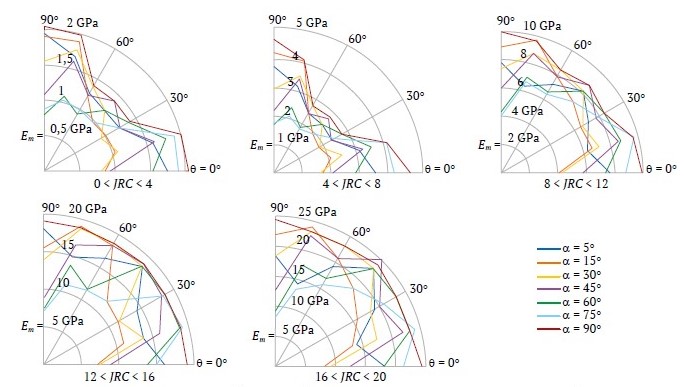
Рис. 11. Модуль деформации блочных массивов горных пород для σci < 25
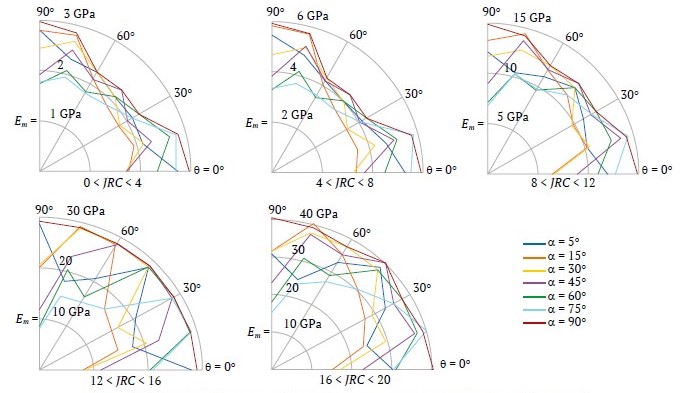
Рис. 12. Модуль деформации блочных массивов горных пород для 25 < σci < 50
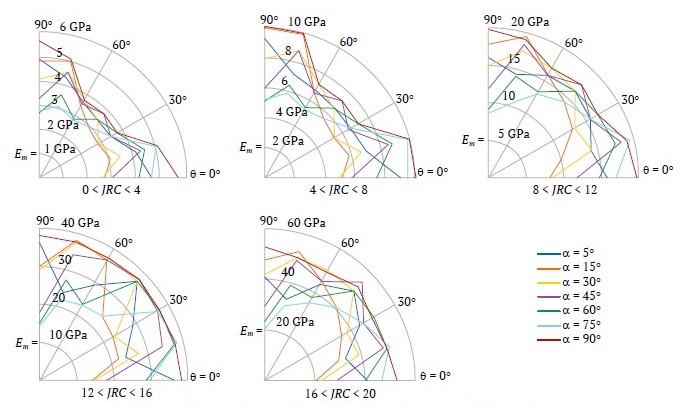
Рис. 13. Модуль деформации блочных массивов горных пород для 50 < σci <100
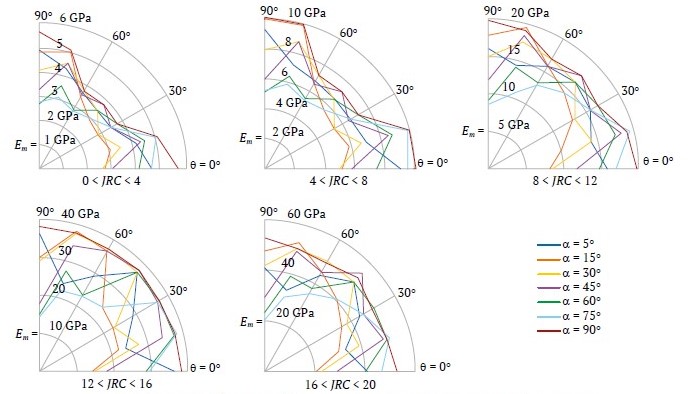
Рис. 14. Модуль деформации блочных массивов горных пород для 100 < σci < 250
3.3. Определение индекса анизотропии в блочных массивах горных пород
Индекс анизотропии RE, обусловленный системой трещин как отношение максимального модуля деформации Emax к минимальному модулю деформации Emin, может быть определен как:
RE был рассчитан для каждой кривой на рис. 11–14. Результаты представлены на рис. 15. Так, на рис. 15, а в первом столбце RE = 1,64 соответствует анизотропии блочного массива горных пород с α = 5°, 0 < JRC < 4 и σci < 25 МПа. Это среднее значение RE рассчитано для пар JRC, σci при JRC = 1, 2, 3, 4 и σci = 5, 10, 15, 20, 25 МПа. Для каждого столбца значения представлены в виде столбиков над ним. Величина индекса анизотропии для блочного массива может находиться в пределах от 1,6 до 2,3 (1,6 ≤ RE ≤ 2,3) при среднем значении 1,88.
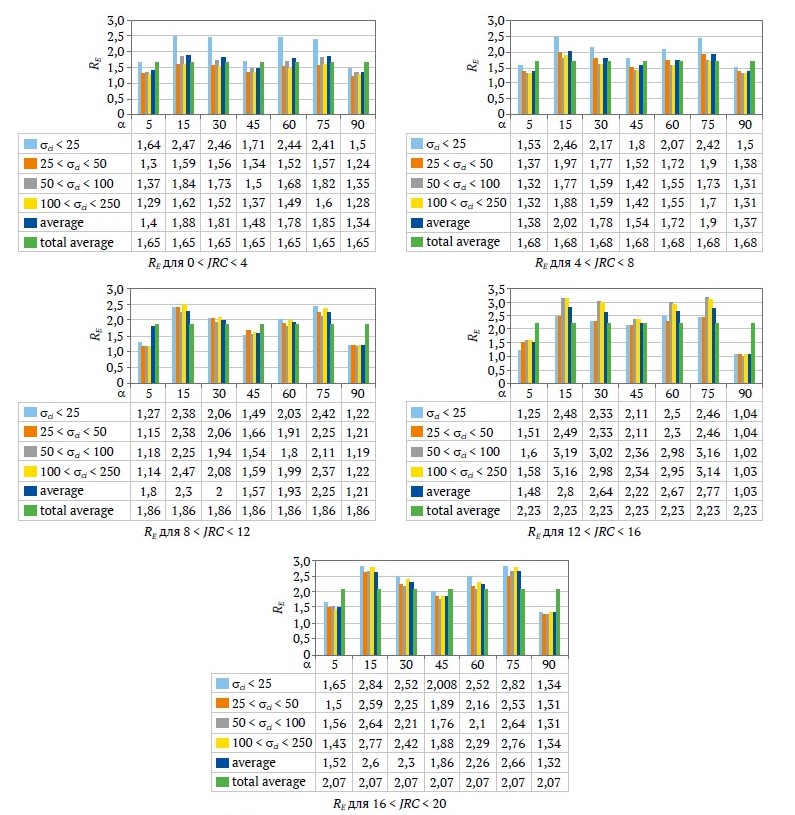
Рис. 15. Степень анизотропии RE блочных массивов горных пород
3.4. Сравнение результатов с эмпирическими соотношениями
Для дальнейшей оценки результатов, представленных на рис. 11–14, приведены диапазоны изменения модуля деформации для каждого класса блочного массива горных пород, которые сравниваются с соответствующими результатами эмпирических соотношений в табл. 5. В этой таблице классификация блочных массивов основана на состоянии поверхности трещин аналогично таблице GSI [17]. Для каждого класса массива (с заданным диапазоном JRC) было выполнено сравнение значений Em, которые были рассчитаны для различных диапазонов σci, а максимальные и минимальные значения приведены в таблице.
В табл. 5 каждому классу массива горных пород на основании значений JRC по аналогии с таблицей GSI Хука (1997) [17] присвоен диапазон GSI.
Из табл. 5 следует, что соотношение, предложенное в [8], при D = 0 ( D – коэффициент разрушения массива породы. Его значение равно нулю для ненарушенного состояния, D = 0,5 для частично нарушенного и D = 1 для полностью нарушенного состояния) демонстрирует наилучшее соответствие результатам численного моделирования. Графически это показано на рис. 16. В табл. 5 значения модуля, полученные на основе соотношения, предложенного в [6], выше, чем в текущем исследовании, однако значения соотношения Гокеоглу и др. (Gokceoglu et al.) [7] ниже, чем результаты текущего моделирования. Кроме того, модули деформации, полученные на основании соотношения [35, 36], высоки по сравнению с результатами текущего исследования для блочного массива горных пород со слабыми трещинами. Однако для прочных трещин значения модулей ниже. Иными словами, по данному соотношению коэффициент безопасности будет очень высоким для слабых трещин и очень низким для прочных трещин.
Таблица 5
Сравнение модулей деформации блочных массивов горных пород Em, оцененных по некоторым эмпирическим соотношениям и посредством численного моделирования
| Состояние поверхности трещины | Весьма непрочное | Нарушенное | Относительно ненарушенное | Ненарушенное | Весьма прочное | Ссылка |
| JRC | 0 < <4 | 4 < < 8 | 8 < < 12 | 12 < < 16 | 16 < < 20 | |
| Deformation modulus (GPa) | ||||||
| Численное моделирование | 0.79–6.2 | 1.6–11.5 | 4–27.5 | 7–54.2 | 8–75.5 | – |
| GSI | 25–45 | 35–55 | 45–65 | 55–75 | 65–85 | – |
| 10(RMR – 10)/40 | 3.16–10 | 5.6–17.7 | 10–31.6 | 17.7–56.2 | 31.6–100 | [6] |
| 2RMR – 100 | – | – | – | 0–60 | 40–80 | [33] |
| 0.1451e0.654GSI | 0.744–2.752 | 1.43–5.29 | 2.75–10.18 | 5.29–19.58 | 10.18–37.66 | [7] |
| 0.0736e0.755RMR | 0.7–3.2 | 1.5–6.8 | 3.2–14.5 | 6.8–30.9 | 4.5–65.7 | [7] |
| 0.33e0.064GSI | 1.63–5.87 | 3.1–11.14 | 5.87–21.14 | 11.14–40.1 | 21.14–76.04 | [34] |
| EiS1/4 | 6.22–10.85 | 8.21–14.32 | 10.85–18.91 | 14.32–24.96 | 18.91–32.96 | [35] |
| Ei(Sα)0,4 | 8.61–14.49 | 11.37–18.38 | 14.49–22.95 | 18.38–28.76 | 22.95–35.85 | [36] |
| 1.05–6.13 | 2.56-13.96 | 6.13–28.73 | 13.96–50 | 28.73–71.42 | [8] | |
| 0.254–1.54 | 0.629–3.71 | 1.54–8.59 | 3.71–18.23 | 8.59–33.27 | [8] | |
| 0.055–0.334 | 0.135–0.823 | 0.334–1.96 | 0.823–4.68 | 1.96–10.21 | [8] | |
GSI = RMR – 5, s = exp [(GSI – 100)/9]
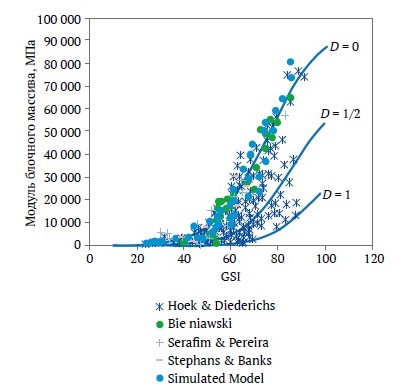
Рис. 16. Сравнение оценки модуля деформации массива горных пород по некоторым эмпирическим соотношениям и посредством численного моделирования
3.5. Модуль деформации и индекс анизотропии блочных массивов в зависимости от GSI
Результаты расчета модуля деформации Em и индекса анизотропии RE блочных массивов можно свести в таблицу GSI, представленную на рис. 17. Значения JRC в этой таблице зависят от качества поверхности трещин.
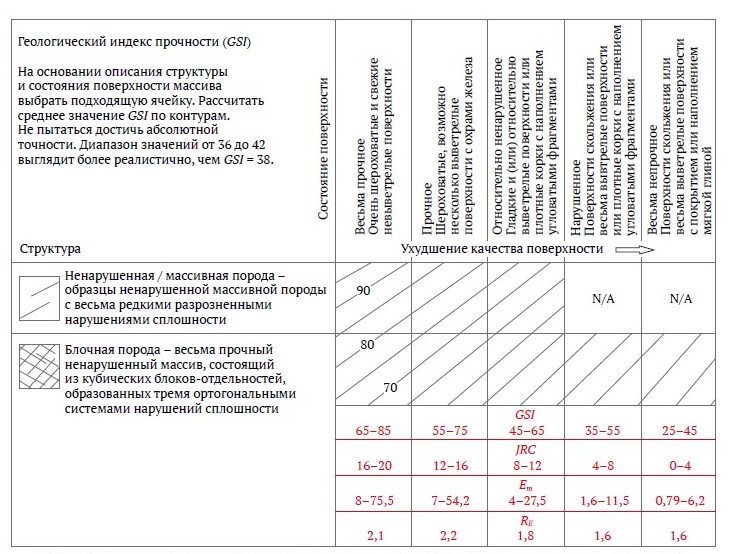
Рис. 17. Модуль деформации Em, степень анизотропии RE и JRC для блочных массивов в таблице GSI
Рис. 11–14 показывают, что если принять JRC постоянным в каждом столбце таблицы GSI, то при увеличении одного интервала в σci значение Em увеличится в среднем в восемь раз. С другой стороны, для конкретного значения σci увеличение JRC на один интервал приведет в среднем к 24-кратному увеличению модуля деформации.
Из этого можно сделать вывод, что влияние качества трещин на модуль деформации блочных массивов выше, чем у прочности ненарушенной породы.
Так, согласно табл. 6, при фиксированном интервале 50 < σci <100 при увеличении JRC с 0 до 20 модуль деформации увеличивается в среднем с 2,5 ГПа до 50 ГПа, что составляет увеличение примерно в 20 раз. Для 8 < JRC < 12 при увеличении σci с σci < 25 МПа до σci < 250 МПа средний модуль деформации для массива увеличивается с 4 ГПа до 27,5 ГПа. Это увеличение примерно в 6,8 раза. В соответствии с вышесказанным можно утверждать, что влияние шероховатости трещины примерно в три раза превышает влияние UCS ненарушенной породы.
Таблица 6
Модуль деформации массива горных пород в зависимости от JRC и σci
| GSI | 25–45 | 35–55 | 45–65 | 55–75 | 65–85 | Восьмикратное увеличение модуля деформации в среднем |
| JRC | 0–4 | 4–8 | 8–12 | 12–16 | 16–20 | |
| σci | Deformation of modulus (GPa) | |||||
| σci < 25 | 0.79–1.75 | 1.6–4 | 4–10 | 7–19 | 8–23 | |
| 25< σci <50 | 1.75–2.8 | 2.75–6 | 7–14.5 | 8–29 | 17–40 | |
| 50< σci <100 | 2.5–5 | 5.2–10 | 8–19.5 | 15–38 | 20–50 | |
| 100< σci <250 | 3.7–6.2 | 6.7–11.5 | 12–27.5 | 18–54.2 | 22–75.5 | |
| 24-кратное увеличение модуля деформации в среднем | ||||||
Заключение
Выполнено систематическое исследование анизотропии в деформационном поведении блочных массивов горных пород методом дискретных элементов. Массив имеет две ортогональные системы трещин, секущиеся третьей системой. Третья система трещин образует переменный угол со второй системой трещин, а ее простирание нормально к простиранию первой системы трещин. Элементы с представительным объемом массивов нагружались одноосно в разных направлениях.
Введены и использованы в моделировании новые нелинейные зависимости от напряжения для нормальной жесткости и жесткости на сдвиг трещин. Независимыми переменными этих зависимостей являются JRC и UCS ненарушенной породы. Коэффициенты нормальной жесткости и жесткости на сдвиг трещин играют важную роль в управлении общим деформационным поведением массива горных пород. Установлено, что влияние нормальной жесткости на модуль деформации массива горных пород примерно в два раза превышает влияние жесткости на сдвиг. Также установлено, что при оценке модуля деформации относительная важность шероховатости трещин намного выше, чем у UCS ненарушенной породы.
Важным моментом в отношении трещин является вероятность наличия маломощных слоев в трещинах. В данном исследовании влияние заполнителя трещин могло быть отражено в JRC, как видно из первой строки табл. 6. Однако связность и коэффициент трения на поверхностях трещин из-за наличия маломощных слоев, которые могут оказывать существенное влияние на результаты моделирования, подробно не рассматривались. В связи с этим Вознесенский и др. [37] провели комплексное исследование, в котором обсуждалось существенное влияние маломощных слоев углеродистых глин на сопротивление контактному растрескиванию различных пород.
Численные исследования показали, что при оценке модуля деформации и режимов разрушения массив с L/S ≥ 10 может быть принят за представительный элементарный объем (REV) для блочного массива горных пород.
Модуль деформации, режим разрушения и поведение после разрушения блочных массивов пород были оценены для различных относительных нагружений и углов трещин. Степень анизотропии модуля деформации (за счет систем разрушения), представленная индексом анизотропии RE, была определена как 1,6 ≤ RE ≤ 2,3 при среднем значении 1,88 в блочных массивах.
При режиме разрушения блочного массива «скольжение по трещинам» деформация текучести составляет около 0,2–0,4. Она не зависит от угла нагружения и направления третьей системы трещин.
Результаты расчетов представлены в виде полярных кривых изменения модуля деформации блочного массива, зависящих от JRC трещин, UCS ненарушенной породы и структуры массива горных пород по относительному углу наклона трещин. Данные кривые позволяют оценить модуль деформации блочного массива в различных направлениях без проведения лабораторных и полевых испытаний или эмпирических соотношений.
В таблице GSI результаты классифицированы таким образом, что, присвоив значение JRC каждому классу состояния поверхности трещин, можно определить модуль деформации и степень анизотропии, соответствующие значениям GSI.
Список литературы
1. Singh B. Continuum characterization of jointed rock masses: Part I – The constitutive equations. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. 1973;10(4):311–335. https://doi.org/10.1016/0148-9062(73)90041-7
2. Gerrard C. M. The equivalent elastic properties of simplified and jointed rock masses. In: Beer G., Brooker J. R., Carter J. P. (Eds.) Proceedings of the 17th International Conference on Computer Methods and Advances in Geomechanics. May 6–10, 1991. Cairns, Australia. Rotterdam: A. A. Balkemam, Brookfield; 1991. Pp. 333–337.
3. Oda M. An experimental study of the elasticity of mylonite rock with random cracks. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. 1988;25:59–69.
4. Amadei B., Savage W. Z. Effect of joints on rock mass strength and deformability. In: Hudson J. A. (Ed.) Comprehensive Rock Engineering – Principle, Practice and Projects. Vol. 1. Oxford, UK: Pergamon; 1993. Pp. 331–365.
5. Kulhawy F. H. Geomechanical model for rock foundation settlement. Journal of the Geotechnical Engineering Division. 1978:104(2):211–227. https://doi.org/10.1061/AJGEB6.0000582
6. Serafim J. L., Pereira J. P. Consideration of the geomechanical classification of Bieniawski. In: Proceedings of the International Symposium on Engineering Geology and Underground Construction. Vol. 1. September 12–15, 1983. Lisbon, Portugal; 1983. Pp. 33–44.
7. Gokceoglu C., Sonmez H., Kayabasi A. Predicting the deformation moduli of rock masses. International Journal of Rock Mechanics and Mining Sciences. 2003;40(5):701–710. https://doi.org/10.1016/S1365-1609(03)00062-5
8. Hoek E., Diederichs M. S. Empirical estimation of rock mass modulus. International Journal of Rock Mechanics and Mining Sciences. 2006;43(2):203–215. https://doi.org/10.1016/j.ijrmms.2005.06.005
9. Heuze F. E. Scale effects in the determination of rock mass strength and deformability. Rock Mechanics. 1980;12:167–192. https://doi.org/10.1007/BF01251024
10. Agharazi A., Derek Martin C., Tannant D. A three-dimensional equivalent continuum constitutive model for jointed rock masses containing up to three random joint sets. Geomechanics and Geoengineering. 2012;7(4):227–238. https://doi.org/10.1080/17486025.2012.714476
11. Cundall P. A. A computer model for simulating progressive large scale movements in blocking rock systems. In: Proceedings of the Symposium of the International Society on Rock Mechanics. France. 1971.
12. Lemos J. V., Hart R. D., Cundall P. A. A generalized distinct element program for modeling jointed rock mass. In: Stephansson O. (Ed.) Proceedings of the International Symposium on Fundamentals of Rock Joints. 15–20 September 1985. Bjorkiden, Sweden; 1985. Pp. 335–343.
13. Cundall P. A. Formulation of a three-dimensional distinct element model – Part I. A scheme to detect and represent contacts in a system composed of many polyhedral blocks. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. 1988;25(3):107–116. https://doi.org/10.1016/0148-9062(88)92293-0
14. Kulatilake P. H. S. W., Wang S., Stephansson O. Effect of finite size joints on the deformability of jointed rock in three dimensions. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. 1993;30(5):479–501. https://doi.org/10.1016/0148-9062(93)92216-D
15. Min K. B., Jing L. Numerical determination of the equivalent elastic compliance tensor for fractured rock masses using the distinct element method. International Journal of Rock Mechanics and Mining Sciences. 2003;40(6):795–816. https://doi.org/10.1016/S1365-1609(03)00038-8
16. Ivars D. M., Pierce M. E., Darcel C. et al. The synthetic rock mass approach for jointed rock mass modelling. International Journal of Rock Mechanics and Mining Sciences. 2011;48(2):219–244. https://doi.org/10.1016/j.ijrmms.2010.11.014
17. Hoek H., Brown E. T. Practical estimates of rock mass strength. International Journal of Rock Mechanics and Mining Sciences. 1997;34(8):1165–1186. https://doi.org/10.1016/S1365-1609(97)80069-X
18. Goodman R. E., Taylor R. L., Brekke T. L. A model for the mechanics of jointed rock. Journal of the Soil Mechanics and Foundations Division. 1968;94(3):637–659. https://doi.org/10.1061/JSFEAQ.0001133
19. Bandis S. C., Lumsden A. C., Barton N. R. Fundamentals of rock joint deformation. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. 1983;20(6):249–268. https://doi.org/10.1016/0148-9062(83)90595-8
20. Duncan J. M., Chang C. Y. Nonlinear analysis of stress and strain in soil. Journal of the Soil Mechanics and Foundations Division. 1970;96(5):1629–1655. https://doi.org/10.1061/JSFEAQ.000145
21. Priest S. D. Discontinuity analysis for rock engineering. London etc.: Chapman & Hall; 1993.
22. Barton N., Choubey V. The shear strength of rock joints in theory and practice. Rock Mechanics and Rock Engineering. 1977;10:1–54. https://doi.org/10.1007/BF01261801
23. Barton N. R. Review of a new shear strength criterion for rock joints. Engineering Geology. 1973;7(4):287–332. https://doi.org/10.1016/0013-7952(73)90013-6
24. Barton N. R. The shear strength of rock and rock joints. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. 1976;13(9):255–279. https://doi.org/10.1016/0148-9062(76)90003-6
25. Barton N. R., Bandis S. C. Review of predictive capabilities of JRC-JCS model in engineering practice, In: Barton N., Stephansson O. (Eds.) Proceedings of the International Symposium on Rock Joints. November 1990, Loen, Norway. Rotterdam: Balkema; 1990. Pp. 603–610.
26. Deere D. U., Miller R. P. Engineering classification and index properties for intact rock. Technical Report No. AFWL-TR-65-116. Air Force Weapons Laboratory (WLDC). Kirtland Air Base, New Mexico; 1966.
27. Robertson A. The interpretation of geological factors for use in slope theory. In: Planning Open Pit Mines, Proceding of the Symposium on the Theoretical Background to the Planning of Open Pit Mines with Special Reference to Slope Stability. August 29–September 4, 1970, Johannesburg, South Africa. A. A. Balkema; 1970. Pp. 55–71.
28. Goodman R. E. Introduction to Rock Mechanics. 2nd Edition. New York: John Wiley & Sons Ltd.; 1989.
29. Cuba A. Personal Communication. 1990.
30. Schultz R. A. Relative scale and the strength and deformability of rock messes. Journal of Structural Geology. 1996;18(9):1139–1149.
31. Jaeger J. C., Cook N. G. W., Zimmerman R. W. Fundamentals of rock mechanics. Oxford: Blackwell Publishing Ltd.; 2007.
32. Yang Z. Y., Chen J. M., Huang T. H. Effect of joint sets on the strength and deformation of rock mass models. Effect of joint sets on the strength and deformation of rock mass models. International Journal of Rock Mechanics and Mining Sciences. 1998;35(1):75–84. https://doi.org/10.1016/s1365-1609(98)80024-5
33. Bieniawski Z. T. Determining rock mass deformability: experience from case histories. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. 1978;15(5):237–247. https://doi.org/10.1016/0148-9062(78)90956-7
34. Hoek E. Practical Rock Engineering. Revision version. 2004.
35. Carvalho J. Estimation of rock mass modulus. Personal communication. 2004.
36. Sonmez H., Gokceoglu C., Ulusay R. Indirect determination of the modulus of deformation of rock mass based on the GSI system. International Journal of Rock Mechanics and Mining Sciences. 2004;41(5):849–857. https://doi.org/10.1016/j.ijrmms.2003.01.006
37. Voznesenskii A. S., Osipov Yu. V., Ushakov E. I. et al. Effect of weak inclusions on the fracture toughness of interfaces between various rocks. Engineering Failure Analysis. 2023;146:107140. https://doi.org/10.1016/j.engfailanal.2023.107140
Об авторах
O. АхрамиИран
Омид Ахрами – аспирант
г. Тегеран
Х. Джавахери Купаи
Иран
Хоссейн Джавахери Купаи – доцент
г. Тегеран
К. Ахангари
Иран
Каве Ахангари – профессор
Scopus ID 36130116400
г. Тегеран
Рецензия
Для цитирования:
Ахрами O., Джавахери Купаи Х., Ахангари К. Определение модуля деформации и характеристик анизотропного поведения блочных массивов горных пород. Горные науки и технологии. 2024;9(2):116-133. https://doi.org/10.17073/2500-0632-2023-08-143
For citation:
Ahrami O., Javaheri Koupaei H., Ahangari K. Determination of deformation modulus and characterization of anisotropic behavior of blocky rock masses. Mining Science and Technology (Russia). 2024;9(2):116-133. https://doi.org/10.17073/2500-0632-2023-08-143




































