Перейти к:
Модель годографа электромагнитных волн, дифрагированных на локальном объекте при георадиолокационном изучении слоев горных пород криолитозоны
https://doi.org/10.17073/2500-0632-2023-05-118
Аннотация
В георадиолокации одной из наиболее популярных процедур определения скорости распространения электромагнитных волн в массиве горных пород является подбор теоретических гиперболических годографов с последующим сравнением с годографом, полученным при георадиолокационном измерении. Эта процедура основана на модели однородной среды, но в настоящее время объектом изучения георадиолокации часто становятся неоднородные среды, такие как горизонтально-слоистые среды, характерные для рыхлых отложений криолитозоны. В статье представлены результаты исследования формирования гиперболических годографов георадиолокационных сигналов в горизонтально-слоистой среде без учета дисперсии и поглощения электромагнитных волн. На основе законов геометрической оптики выведены формулы, позволяющие рассчитать форму гиперболической оси синфазности георадиолокационных сигналов, отраженных от локального объекта в многослойном массиве мерзлых горных пород. На примере массива горных пород криолитозоны, содержащего слой незамерзших горных пород, показано влияние мощностей слоев горных пород и их относительной диэлектрической проницаемости на кажущуюся диэлектрическую проницаемость, получаемую в результате расчета теоретического гиперболического годографа. Также представлены условия, при которых невозможно определить наличие слоя незамерзших горных пород по гиперболическому годографу. Установленные закономерности апробированы на синтетических георадиолокационных радарограммах, рассчитанных в программе gprMax. Результаты теоретических исследований подтверждены сравнением с результатами анализа данных компьютерного моделирования георадиолокационных измерений в системе gprMax (относительная погрешность составила менее 0,5 %).
Ключевые слова
Для цитирования:
Соколов К.О. Модель годографа электромагнитных волн, дифрагированных на локальном объекте при георадиолокационном изучении слоев горных пород криолитозоны. Горные науки и технологии. 2024;9(3):199-205. https://doi.org/10.17073/2500-0632-2023-05-118
For citation:
Sokolov K.О. Model of time-distance curve of electromagnetic waves diffracted on a local feature in the georadar study of permafrost zone rock layers. Mining Science and Technology (Russia). 2024;9(3):199-205. https://doi.org/10.17073/2500-0632-2023-05-118
Модель годографа электромагнитных волн, дифрагированных на локальном объекте при георадиолокационном изучении слоев горных пород криолитозоны
Введение
Одной из геофизических задач, решаемых с привлечением метода георадиолокации, является исследование физико-механических свойств горных пород. Однако накопление экспериментальных материалов и развитие методического обеспечения георадиолокации в данном направлении происходит существенно медленнее [1, 2], чем в других [3], что приводит к недооценке возможностей метода георадиолокации. Причины, приведшие к такому положению дел в георадиолокации, могут быть различные, одной из них является некорректное использование процедуры определения скорости v распространения электромагнитных волн (ЭМВ) по гиперболическим годографам (осям синфазности георадиолокационных сигналов). Данная процедура является наиболее распространенным способом оценки скорости ЭМВ [1], по результатам выполнения которой рассчитывается вещественная часть относительной комплексной диэлектрической проницаемости ε′, зависящая от влажности, плотности и криогенного состояния горных пород [4]. В учебных пособиях как отечественных [1, 2], так и зарубежных [5, 6], а также в руководствах по обработке данных производителей георадаров (GSSI, ГЕОТЕХ) и стандарте American Society for Testing and Materials (ASTM)1 обоснование применения определения скорости распространения ЭМВ по гиперболическим годографам приводится для случая, когда вмещающая среда является однородной.
В настоящее время в практике георадиолокационных измерений [3, 7, 8], а также в научных работах, посвященных автоматизации поиска гиперболических годографов в данных георадиолокации [9–11], в том числе в режиме реального времени [12], объектом исследования является, как правило, неоднородная среда. Вследствие этого скорость распространения ЭМВ, определенная по гиперболе, находящейся в некотором слое, является усредненной (интегральной) характеристикой всех вышележащих слоев, о чем упомянуто в работе одного из классиков георадиолокации [13]. При проведении георадиолокационных исследований в области криолитозоны возможна неверная оценка криогенного состояния горных пород и, соответственно, их физико-механических свойств, в случае наличия слоя незамерзших горных пород, влияние которого на форму гиперболического годографа может быть хотя и значительным, но недостаточным для того, чтобы результат определения v по методу аппроксимации годографа гиперболой [2] оказался в диапазоне значений, характерных для талых пород. Таким образом, в многослойной среде непосредственно по гиперболическому годографу возможно определить истинную скорость v распространения ЭМВ только в первом слое горных пород, и для корректного использования значений v в практике ведения георадиолокационных работ необходимо установить закономерности формирования в слоистых породных массивах годографов ЭМВ, дифрагированных на локальном объекте. Для достижения указанной цели необходимо решить следующие задачи:
- разработать модель гиперболического годографа сигналов, получаемых при изучении слоистого породного массива;
- установить зависимость v и ε′, определяемых по гиперболическому годографу, от значений v и ε′ вышележащих слоев;
- определить влияние незамерзшего слоя в массиве мерзлых горных пород на значение v, рассчитываемое по гиперболическому годографу;
- проверить адекватность полученных теоретических результатов на данных компьютерного моделирования.
1 ASTM D6432-11, Standard guide for using the surface ground penetrating radar method for subsurface investigation, ASTM International, West Conshohocken, PA; 2011. https://doi.org/10.1520/D6432-11
Модель гиперболического годографа георадиолокационных сигналов, получаемых при зондировании слоистого породного массива
ЭМВ, излучаемая георадаром, расположенном в точке х, распространяется в слоистом породном массиве по принципу Ферма (серая сплошная линия на рис. 1), но в данной работе рассмотрим модель распространения ЭМВ по лучу (черная пунктирная линия на рис. 1) в массиве, состоящем из n слоев мощностью hi с заданными значениями ε′i и vi, при i, находящемся в диапазоне от 1 до n. Локальный объект, обозначенный черным кружком на рис. 1, расположен в последнем слое на глубине h0. Расстояние hл, пройденное лучом от георадара до локального объекта, будет равно:

При перемещении георадара вдоль профиля координата х будет увеличиваться, а hл соответственно уменьшаться, формируя левую ветвь гиперболы и достигая минимума в точке х = х0, в которой и будет расположена вершина гиперболы. При х > х0 значения hл будут увеличиваться и соответствовать правой ветви гиперболы. В промежуточном слое под номером i луч проходит расстояние hлi, которое больше мощности слоя hi во всех точках, кроме х0:

где

Так как в последнем слое луч проходит расстояние меньшее, чем hn, то hлn будет равно:

Время распространения луча в слое i:


Рис. 1. Схема модели распространения электромагнитной волны в слоистом породном массиве
Общее время tл распространения луча от георадара до локального объекта составит:

Тогда усредненная лучевая скорость будет равна:

Уравнение гиперболического годографа в однородной среде [2]:
![]()
Для горизонтально-слоистой среды уравнение (1) примет следующий вид:

Исходя из основного тригонометрического тождества и положительности функции косинуса в области значений арксинуса преобразуем знаменатель дроби:
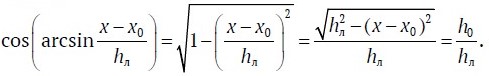
Тогда уравнение гиперболического годографа георадиолокационных сигналов, отраженных от локального объекта, расположенного в слоистом породном массиве, может быть представлено в виде (2). При подстановке в уравнение (2) параметров для однослойной среды оно совпадает с выражением (1):
![]()
При обработке данных георадиолокации гиперболический годограф, имеющий форму, соответствующую выражению (2), аппроксимируют гиперболой, имеющей вид согласно уравнению (1). Рассчитываемые в результате подобной аппроксимации значения скорости распространения ЭМВ являются не истинными, а кажущимися (vкаж), и представляют собой некоторое интегральное значение скоростей ЭМВ во всех вышележащих слоях. Для определения зависимости vкаж от значений v в слоях, перекрывающих локальный объект, приравняем друг к другу уравнения (1) и (2):

И выразим vкаж:

И в соответствии с известной зависимостью v = c/√ε′ (с = 300 000 км/с = 0,3 м/нс) [2] кажущаяся диэлектрическая проницаемость будет равна:

По значению vкаж невозможно оценить скорость распространения ЭМВ в горных породах конкретного слоя и может возникнуть предположение, что v каждого слоя находится в диапазоне vкаж ± Δv. Например, если при проведении георадиолокационных измерений массива многолетнемерзлых горных пород, у которых v находится в узком диапазоне 100–150 м/мкс (среднее значение vср ≈ 125 м/мкс) [14], vкаж будет выше 100 м/мкс, то в целом массив можно охарактеризовать как мерзлый. Однако в подобных массивах может находиться слой пород в талом состоянии, который может быть зафиксирован по данным георадиолокации, но существует проблема с его распознаванием [15], в связи с этим возникает проблема определения влияния слоя пород с низким значением vс на vкаж.
Для решения данной проблемы воспользуемся формулой (3) и тем фактом, что v мерзлых горных пород варьируется в узких пределах, а скорость vт распространения ЭМВ в незамерзших горных породах значительно ниже [2]. Часть массива горных пород, находящуюся в мерзлом состоянии, представим в виде слоев одинаковой толщины hс, в каждом из которых скорость распространения ЭМВ будет равна усредненному значению vс. Разбивать мерзлую часть массива горных пород на слои можно произвольно, так как при одинаковой v их количество и толщина не влияют на время регистрации георадиолокационных сигналов, составляющих гиперболическую ось синфазности. Толщину hт и скорость vт в слое талых пород представим пропорциональными hс и vс:
hт = khhс, vт = kvvт.
После подстановки в (3) получим выражение для кажущейся скорости vкаж.т распространения ЭМВ в массиве мерзлых горных пород, содержащем слой пород в талом состоянии:

При kh = 0 по формуле (5) vкаж.т = vс, т.е. будет соответствовать мерзлому массиву горных пород. Для того чтобы определить, как изменится vкаж по сравнению с vс при наличии низкоскоростного слоя талых пород, разделим формулу (3) с параметрами мерзлых пород hс и vс для всех слоев, обозначив ее vкаж.м, на выражение (5):

Проверка полученных теоретических выражений на данных компьютерного моделирования
Моделирование данных георадиолокации проведено в системе gprMax [16], которая положительно зарекомендовала себя в исследованиях, посвященных определению и анализу гиперболических осей синфазности георадиолокационных сигналов [17–19]. При моделировании использовались следующие параметры: зондирующий сигнал – импульс Рикера с центральной частотой Фурье-спектра 400 МГц, временная развертка – 150, база антенны – 0 мм. Данные для моделирования представлены в таблице.
Текст входного файла для gprMax для модели №1:
#domain: 4 9.1 0.002
#dx_dy_dz: 0.002 0.002 0.002
#time_window: 150e-9
#material: 6 0 1 0 sloi1
#material: 4 0 1 0 sloi2
#waveform: ricker 10 0.4e9 my_ricker
#hertzian_dipole: z 0.1 9 0 my_ricker
#rx: 0.1 9 0
#src_steps: 0.01 0 0
#rx_steps: 0.01 0 0
#box: 0 0 0 4 9 0.002 sloi1
#box: 0 0 0 4 7 0.002 sloi2
#cylinder: 2 5 0 2 5 0.002 0.01 pec
Результат моделирования (out-файл) экспортирован в формат программы GeoScan32 (производитель НПЦ ГЕОТЕХ), в которой затем установлены начало отсчета шкалы глубин и параметр База антенны, равный 1. На рис. 2, а представлены результаты моделирования (Модель №1), значения ε′каж, рассчитанной с помощью процедуры «Гипербола», и vкаж. Время регистрации сигналов, отраженных от нижней границы 1 слоя t1 и от локального объекта – вершины гиперболы tг, в соответствии с формулой (1) равно:
t1 = 32,7 нс, tг = t1 + 26,7 = 59,4 нс.
Таблица
Параметры моделей массива горных пород
| № модели | Количество слоев | Мощность слоев, м | ε′ | v, м/мкс | h0, м |
| 1 | 2 | 2; 7 | 6; 4 | 122,5; 150 | 4 |
| 2 | 3 | 2; 2; 4 | 8; 6; 4 | 100; 122,5; 150 | 6 |
| 3 | 5 | 1; 1; 1; 0,5; 2 | 6; 4; 6; 20; 4 | 122,5; 150; 122,5; 67; 150 | 4,5 |
По формулам (3) и (4) vкаж и ε′каж будут равны:
vкаж = 0,1349 м/нс = 134,9 м/мкс; ε′каж = 4,9484.
Проверка полученных значений:
![]()
Таким образом, относительная погрешность значений vкаж и ε′каж, рассчитанных в программе GeoScan32, составила 0,07 и 0,37 % соответственно. Для модели №2 в результате вычислений по формулам (3) и (4) получены значения vкаж = 123,7 м/мкс, ε′каж = 5,8853.
Для проверки формулы (6) сначала проведем вычисления vкаж.м для модели массива мерзлых горных пород мощностью h0 = 5 м, состоящей из n = 5 слоев с h = 1 м, v = 122,5, 150, 122,5, 134,2, 150 м/мкс и ε′ = 6; 4; 6; 5; 4. Согласно выражению (3) vкаж.м = 134,7 м/мкс.
Далее вместо четвертого слоя введем низкоскоростной слой (модель №3 в таблице) с такими параметрами hт, vт, чтобы значение vкаж.т находилось в диапазоне, характерном для мерзлых горных пород. Установим мощность незамерзшего слоя hт = 0,5 м (при этом h0 уменьшится до 4,5 м) как половину (kh = 0,5) мощности усредненного слоя hс = 1 м, а скорость распространения ЭМВ в нем в два раза меньше (kv = 0,5), чем среднее значение ε′с = 5, vс = 134,2 м/мкс, т. е. vт = 67,1 м/мкс, ε′т = (c/vт)2 = 20. Остальные параметры моделируемого массива горных пород представлены в таблице. По формуле (3) vкаж.т = 121,2 м/мкс, что подтверждается результатом вычисления vкаж по данным компьютерного моделирования (рис. 2, в), относительная погрешность которого, по сравнению с точным значением, составила менее 0,5 %.

Рис. 2. Синтетические радарограммы моделей 1 (а), 2 (б) и 3 (в)
Теперь можно рассчитать, как изменилась кажущаяся скорость распространения ЭМВ в модели массива горных пород с введением в нее низкоскоростного слоя:
![]()
То есть при наличии низкоскоростного слоя с указанными выше параметрами vкаж уменьшается на ≈10 %. Для получения данного результата пришлось провести весь комплекс расчетов по вычислению vкаж как для полностью мерзлого массива горных пород, так и для случая со слоем незамерзших пород. Подобные расчеты можно существенно упростить, если использовать формулу (6), позволяющую с точностью до тысячных получить тот же результат:

Для подтверждения того, что формула (6) верна при разбиении мерзлой части массива горных пород на произвольное количество слоев, проведены расчеты для модели с 3 и 9 слоями. При этом будет изменяться только один параметр – kh, так, при n = 3 (h = 2, 0,5, 2 м) kh = 0,25, при n = 9 (мощность всех слоев – 0,5 м) kh = 1:

В общем случае, чтобы определить, будет ли vкаж.т находиться в диапазоне значений, характерных для мерзлых пород, например, Центральной Якутии, при произвольных kh, kv в формулу (5) подставим усредненные значения, характерные для этого района, vс = 125 м/мкс и vкаж.т = 100 м/мкс [14], тогда при весьма значительной разнице между vкаж.м и vкаж.т:
![]()
получим из (5):
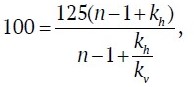
откуда

При увеличении vкаж.т или уменьшении vкаж.м выражение (7) будет больше 0,8, а соотношение vкаж.м/vкаж.т будет уменьшаться, что приведет к затруднениям при интерпретации данных георадиолокационных измерений по определению наличия слоя незамерзших горных пород на основе анализа гиперболического годографа георадиолокационных сигналов. Оценка возможности выявления слоя незамерзших горных пород, в зависимости от величин параметров kh, kv по формуле (7), сделана для района Центральной Якутии, для других районов ее необходимо пересчитать с соответствующими значениями скоростей распространения ЭМВ в мерзлых и талых горных породах.
Выводы
В результате проведенного исследования разработана модель гиперболического годографа георадиолокационных сигналов, отраженных от локального объекта, расположенного в массиве горных пород, с произвольным количеством слоев. На основе разработанной модели получены выражения для кажущихся значений скорости распространения электромагнитных волн и вещественной части относительной комплексной диэлектрической проницаемости рассчитываемых по гиперболическому годографу георадиолокационных сигналов. Полученные выражения позволили установить, как снизится скорость распространения электромагнитных волн в массиве горных пород, содержащем слой незамерзших горных пород, по сравнению с полностью мерзлым массивом. Результаты теоретических исследований подтверждены сравнением с результатами анализа данных компьютерного моделирования георадиолокационных измерений в системе gprMax (относительная погрешность составила менее 0,5 %).
Полученные в ходе исследования результаты имеют большое значение для развития методического обеспечения георадиолокации по определению электрофизических свойств горных пород, что повысит достоверность оценки их физико-механических свойств, особенно в области распространения вечной мерзлоты. Практическое применение полученных результатов в исследованиях, направленных на автоматизированное определение электрофизических свойств горных пород и грунтов по гиперболическим годографам, позволит сформировать базу данных с актуальной информацией о диэлектрической проницаемости горных пород.
Список литературы
1. Старовойтов А. В. Интерпретация георадиолокационных данных. М.: Изд-во МГУ; 2008. 192 с.
2. Владов М. Л., Судакова М. С. Георадиолокация. От физических основ до перспективных направлений. М.: Изд-во ГЕОС; 2017. 240 с.
3. Lombardi F., Podd F., Solla M. From its core to the niche: insights from GPR applications. Remote Sens. 2022;14(13):3033. https://doi.org/10.3390/rs14133033
4. Фролов А. Д. Электрические и упругие свойства мерзлых пород и льдов. Пущино: ОНТИ ПНЦ РАН; 1998. 515 с.
5. Persico R. Introduction to ground penetrating radar: inverse scattering and data processing. New Jersey: Wiley-IEEE Press; 2014. 392 с. https://doi.org/10.1002/9781118835647.ch2
6. Jol H. M. Ground penetrating radar: theory and application. Elsevier; 2008. 544 p. https://doi.org/10.1016/B978-0-444-53348-7.X0001-4
7. Дьяков А. Ю., Калашник А. И. Методические основы георадарных исследований горнотехнических объектов. Апатиты: Изд-во ФИЦ КНЦ РАН; 2021. 110 с. https://doi.org/10.37614/978.5.91137.443.3
8. Solla M., Perez-Gracia V., Fontul S. A review of GPR application on transport infrastructures: troubleshooting and best practices. Remote Sens. 2021;13(4):672. https://doi.org/10.3390/rs13040672
9. Wunderlich T., Wilken D., Majchczack B. S. et al. Hyperbola detection with retinanet and comparison of hyperbola fitting methods in GPR data from an archaeological site. Remote Sensing. 2022;14:3665. https://doi.org/10.3390/rs14153665
10. Mertens L., Persico R., Matera L., Lambot S. Automated detection of reflection hyperbolas in complex gpr images with no a priori knowledge on the medium. In: IEEE Transactions on Geoscience and Remote Sensing. 2016;1:580–596. https://doi.org/10.1109/TGRS.2015.2462727
11. Lei W., Hou F., Xi J. et al. Automatic hyperbola detection and fitting in GPR B-scan image. Automation in Construction. 2019;106:102839. https://doi.org/10.1016/j.autcon.2019.102839
12. Dou Q., Wei L., Magee R., Cohn A. G. Real-time hyperbola recognition and fitting in GPR data. In: IEEE Transactions on Geoscience and Remote Sensing. 2017;55(1):51–62. https://doi.org/10.1109/TGRS.2016.2592679
13. Daniels J. J. Fundamentals of ground penetrating radar. In: Symposium on the Application of Geophysics to Engineering and Environmental Problems. 1989;1:62–142. https://doi.org/10.4133/1.2921864
14. Омельяненко А. В., Федорова Л. Л. Георадиолокационные исследования многолетнемерзлых пород. Якутск: Изд-во ЯНЦ СО РАН; 2006. 136 с.
15. Якупов В. С. Геофизика криолитозоны. Якутск: Изд-во Якутского госуниверситета; 2008. 342 с.
16. Warren C., Giannopoulos A., Giannakis I. gprMax: Open source software to simulate electromagnetic wave propagation for Ground Penetrating Radar. Computer Physics Communications. 2016;209:163–170. https://doi.org/10.1016/j.cpc.2016.08.020
17. Wunderlich T., Wilken D., Majchczack B. S., et al. Hyperbola detection with RetinaNet and comparison of hyperbola fitting methods in GPR data from an archaeological site. Remote Sensing. 2022;14:3665. https://doi.org/10.3390/rs14153665
18. Dewantara D., Parnadi W. W. Automatic hyperbola detection and apex extraction using convolutional neural network on GPR data. Journal of Physics: Conference Series. 2022;1:012027. https://doi.org/10.1088/1742-6596/2243/1/012027
19. Wang H., Ouyang S., Liao K.-F., Jin L.-N. GPR B-SCAN image hyperbola detection method based on deep learning. Acta Electronica Sinica. 2021;49(5):953-963. https://doi.org/10.12263/DZXB.20200635
Об авторе
К. О. СоколовРоссия
Кирилл Олегович Соколов – кандидат технических наук, старший научный сотрудник лаборатории георадиолокации
Scopus ID 56457950500, ResearcherID P-8843-2016
г. Якутск
Рецензия
Для цитирования:
Соколов К.О. Модель годографа электромагнитных волн, дифрагированных на локальном объекте при георадиолокационном изучении слоев горных пород криолитозоны. Горные науки и технологии. 2024;9(3):199-205. https://doi.org/10.17073/2500-0632-2023-05-118
For citation:
Sokolov K.О. Model of time-distance curve of electromagnetic waves diffracted on a local feature in the georadar study of permafrost zone rock layers. Mining Science and Technology (Russia). 2024;9(3):199-205. https://doi.org/10.17073/2500-0632-2023-05-118




































