Комплексное исследование анизотропии микроструктурных и фильтрационных свойств коллектора газоконденсатного месторождения на базе цифрового анализа керна

Введение

Современные технологии, основанные на применении методов численного моделирования и рентгеновской микротомографии, предоставляют новые возможности для детального изучения порового пространства коллектора и прогноза его фильтрационно-ёмкостных свойств [1, 2]. Однако традиционные методы оценки (лабораторные измерения на керне [3], гидродинамические исследования скважин, эмпирические корреляции [4]) не учитывают микроструктуру порового каркаса и часто не позволяют надёжно прогнозировать проницаемость только на основе пористости [4]. Это особенно актуально для слабосцементированных песчаников газоконденсатных шельфовых месторождений, для которых стабильность коллектора и эффективность фильтрации [5] часто зависят не только от объёма пор, но и от их пространственной организации [6]. Использование цифровых двойников керна на основе микротомографических данных позволяет воспроизвести топологию порового пространства [7, 8] и повысить достоверность прогноза продуктивности [9].

Одной из ключевых задач цифрового анализа является количественная характеристика параметров, влияющих на фильтрационные процессы, включая открытую и закрытую пористость [7, 9], извилистость [10], структуру перколяционных каналов [11] и направленную (анизотропную) изменчивость этих параметров [12, 13]. Это особенно важно при эксплуатации пластов горизонтальными скважинами, где эффективность дренажа может значительно зависеть от ориентации ствола относительно текстурных особенностей коллектора [14, 15].

Количество и морфология фильтрационных каналов приобретают критическое значение при разработке шельфовых месторождений [16], где эксплуатационные ошибки могут привести к пескопроявлениям, выносу породы и резкому падению проницаемости [17, 18]. В условиях слабосцементированных пород устойчивость стенок скважин [19] и локальная проницаемость определяются не столько средними характеристиками [20], сколько микроструктурными параметрами порового каркаса, включая субструктурную анизотропию [21, 22]. Несмотря на увеличивающуюся значимость учета вышеописанных характеристик большинство исследований ограничиваются изотропными моделями или фокусируются на пористости, не учитывая комплексного влияния морфологии пор на фильтрацию [23, 24].

Целью настоящего исследования является количественное описание анизотропии фильтрационно-ёмкостных свойств, направленный анализ морфометрических характеристик и их связи с проницаемостью для слабосцементированных песчаников продуктивного интервала газоконденсатного месторождения северного шельфа на основе цифровых двойников керна с последующей интерпретацией результатов для задач гидродинамического моделирования, распространения фронта фильтрации в пласте и проектирования направлений горизонтальных скважин. Научная новизна работы заключается в выполнении комплексной цифровой оценки пространственной анизотропии порового пространства с учётом морфологических и физических особенностей коллектора, установлении факта устойчивой субструктурной анизотропии внутри плоскости напластования для рассматриваемого месторождения, обосновании направлений бурения горизонтальных скважин в условиях текстурной неоднородности пласта, выводах о рисках локального накопления давления в пласте и капиллярной изоляции конденсата.

Для достижения цели были поставлены следующие задачи:

• построение цифровых двойников керна по микротомографическим данным высокого разрешения;
• определение открытой и закрытой пористости, извилистости, параметров перколяционных путей и оценка их направленной вариации;
• численное моделирование фильтрационного потока по трём ортогональным направлениям с расчётом проницаемости;
• анализ соотношения между геометрическими характеристиками порового пространства и фильтрационными свойствами;
• определение репрезентативного элементарного объёма (REV) и обоснование достоверности цифровой модели.

1. Методика и объекты исследований

Объектом исследования являлись породы-коллекторы продуктивного пласта газоконденсатного месторождения, расположенного на северном шельфе России. Породы представлены слабосцементированными песчаниками с низкой прочностью, обладающими высокими пористостью и проницаемостью. Коллектор экстрагированный, характеризуется отсутствием выраженного визуального напластования, подвержен интенсивному пескопроявлению. Из продуктивного интервала были отобраны фрагменты керна с последующей подготовкой более 10 образцов произвольной формы с габаритами от 5 до 20 мм. Для исследования порового пространства применялась технология рентгеновской компьютерной микротомографии. Сканирование проводилось с использованием оборудования Procon X-Ray CT-MINI Института проблем механики РАН [9]. Полученные томографические данные представляли собой наборы срезов с разрешением (размер вокселя – кубического пикселя [25]) 4,995 мкм, реконструированных в трёхмерные цифровые модели фрагментов керна. Все образцы имели схожий структурный состав, что подтверждает репрезентативность выборки, однако для последующего цифрового анализа были отобраны образцы с полным отсутствием трещиноватости, которая может быть следствием влияния условий транспортировки и хранения подверженного растрескиванию материала.

После процедуры реконструкции и обработки (включая коррекции яркости Gradient и/или Gaussian Brightness correction [26], фильтрации алгоритмами Non-local Means [27]) выполнялась сегментация [28] томографических снимков для выделения двух фаз: порового пространства (воздуха) и твёрдой матрицы (зерен). Для реконструкции использовалось ПО VGStudio [29], а также авторские алгоритмы для обработки 3D-снимков. Для сегментации использовались пороговые алгоритмы, основанные на анализе гистограммы распределения интенсивностей [28]. В результате формировалась бинарная воксельная модель (цифровой двойник), в которой каждый воксель обозначался либо как поровый, либо как матричный. Такие модели служат основой для последующих вычислений. На рис. 1 показаны основные этапы работы со снимками.

Рис. 1. Основные этапы предобработки и сегментации томографических данных: а – часть проекции реконструированного снимка; б – часть проекции снимка после предварительной обработки и сглаживания; в – эта же область после сегментации на две фазы: серым изображены зерна матрицы, белым – поры

Цифровой анализ порового пространства включал:

• оценку открытой и закрытой пористости в трёх ортогональных направлениях;
• расчет геодезической извилистости (минимальной, максимальной и средней) на основе алгоритмов поиска кратчайших путей от одной грани трехмерной бинарной модели до противоположной;
• выделение и анализ перколяционных путей, включая расчет их длины и диаметра сужений (максимального диаметра проходимой через канал частицы);
• численное моделирование фильтрационного потока на базе модели Навье–Стокса с использованием условий ламинарного течения для оценки проницаемости и распределения потоков в каждом направлении;
• построение визуальных карт скоростей, градиентов давления и распределения пористости по слоям для качественной интерпретации пространственной структуры порового каркаса.

Анализ порового пространства выполнен в среде GeoDict [30]. Открытая и закрытая пористость вычислялась путём подсчёта долей поровых вокселей. Открытая пористость определялась как доля вокселей, которые связаны с одной из внешних граней модели и формируют сквозной путь. Закрытая пористость – это оставшиеся изолированные поры, не соединённые с внешними гранями. Эти значения рассчитывались отдельно по трём ортогональным направлениям.

Геодезическая извилистость оценивалась на основе построения кратчайших путей от одной грани образца до противоположной в каждом направлении. Извилистость определялась как отношение длины пути по поровому пространству к геометрической длине образца.

В отличие от извилистости, которая может учитывать узкие участки, недоступные для реального флюида, алгоритм поиска перколяционных путей строил физически реалистичные траектории, учитывая диаметр проходимой частицы. Алгоритм исключал пути с «горлышками», меньшими заданного диаметра, и отбирал те каналы, по которым частица могла бы пройти, не нарушая непрерывности. Для каждого направления рассчитывались: длина перколяционного пути – действительное расстояние, которое прошла бы частица; максимальный диаметр – минимальный поперечный размер по пути (самое узкое место), определяющий проходимость. В результате визуализации получен набор фильтрационных каналов, соответствующих физическим условиям флюидопроводности. Таким образом, в работе применяется физически ориентированный подход к перколяции, позволяющий выявлять эффективные траектории фильтрационного потока с учётом геометрических ограничений.

На базе бинарной модели проводилось моделирование течения флюида (воздуха) через поровое пространство по уравнениям Навье–Стокса [31] в стационарной ламинарной постановке:

−μΔū + ρ(ū ⋅∇)ū +∇p = ḟ,

где μ – вязкость жидкости, Па·с;  ū – скорость жидкости, м/с; ρ – плотность жидкости, кг/м³; p – давление, Па;  ḟ – объемная сила, Н/м³.

Уравнение сохранения массы в данном случае принимает вид:

∇⋅ū = 0.

Проницаемость материала может быть рассчитана с использованием закона Дарси:

Q = −kA/μ · (P_b − P_a)/L,

где Q – поток жидкости, м³/с; k – проницаемость среды, м²; A – площадь поперечного сечения потока, м²; μ – вязкость жидкости, Па·с; P_b, P_a – давления, Па; L – длина, на которой происходит этот перепад давления, м.

В данном исследовании для численного моделирования фильтрации использовался решатель LIR [32]. Расчёты выполнялись с заданным перепадом давления 100 Па. Критерий завершения вычислений – error bound 0,1 [33]. В направлении расчета выставлялись периодические граничные условия с прослойками в 10 вокселей на входе и выходе для однородности потока. Симметричные граничные условия были выставлены в тангенциальном направлении [33]. На выходе рассчитывались: поля скоростей и давления; интегральное значение проницаемости по каждому направлению (по обобщённому закону Дарси); визуализация скоростных каналов, отражающая активные пути фильтрации. В отличие от традиционных методов оценки проницаемости, таких как лабораторные фильтрационные эксперименты, корреляции типа φ–k, модели Козени–Кармана, используемый подход основан на прямом численном моделировании фильтрации по 3D-данным микротомографии. Он позволяет не только учитывать реальную геометрию порового пространства и анизотропию, но и проводить детальный анализ структуры фильтрационных каналов.

Для качественной оценки неоднородности структуры порового пространства строились картограммы послойной пористости [34]. Модель усреднялась по слоям, перпендикулярным к выбранной оси, а затем пористость отображалась в виде двумерной цветовой карты. Это позволяло выявить вертикальные или горизонтальные флуктуации в структуре и визуально оценить однородность образца.

В дополнение к численному моделированию проводились лабораторные измерения проницаемости по оси керна Z и в плоскости напластования XY на установке ИСТНН ИПМех РАН [9]. Полученные лабораторные значения использовались для валидации цифровой модели и сопоставления с результатами прямого численного расчёта.

2. Результаты и их обсуждение

В табл. 1 приведены сводные результаты цифрового анализа для трёх характерных образцов. Итоговые цифровые образцы представляли собой кубы с габаритами 500 вокселей, по которым выполнялись расчёты фильтрации в трёх взаимно перпендикулярных направлениях – X, Y и Z (ось Z совпадает с продольной осью керна). Таблица включает значения геодезической извилистости (минимальной, максимальной и средней), длины, рассчитанной в ходе оценки извилистости траектории (минимальной, максимальной и средней), параметров перколяционных путей (средний максимальный диаметр частицы и средняя длина физического пути по всем каналам в заданном направлении), а также значения открытой и закрытой пористости, вычисленной проницаемости. Таблица структурирована по образцам: строки сгруппированы по номеру образца, каждая строка соответствует одному направлению моделирования.

Таблица 1

Сводные результаты проведенного цифрового анализа

Полученные данные по пористости демонстрируют высокую однородность порового пространства как в количественном отношении, так и в пространственном распределении. Открытая пористость во всех трёх ортогональных направлениях практически идентична и составляет около 26 % (см. табл. 1), причём различия между направлениями не превышают сотых долей процента. Максимальное значение открытой пористости наблюдается по оси X (≈ 26,007 %), минимальное – по оси Y (≈ 25,995 %), а по оси Z составляет ≈ 26,008 %. Таким образом, разница в открытой пористости между X, Y и Z ничтожно мала (не более 0,013 пп.), что указывает на отсутствие направленной анизотропии открытой пористости и подтверждает текстурную однородность образцов. Стандартное отклонение значений открытой пористости между образцами для каждого направления не превышает 0,005 %, а коэффициент вариации составляет менее 0,02 % – это свидетельствует о высокой воспроизводимости полученных результатов. Закрытая пористость также имеет очень низкие значения (порядка десятых долей процента) и незначительно варьируется между направлениями. Необычно, что по направлению Y она оказалась несколько выше (≈ 0,413 %) по сравнению с Z (≈ 0,204 %) и X (≈ 0,176 %). Такой результат на первый взгляд противоречит ожидаемому влиянию: обычно более высокая доля изолированных пор (закрытая пористость) должна ухудшать фильтрационные свойства. В данном случае, однако, разница настолько мала в абсолютном выражении, что её влияние не прослеживается – направление Y остаётся наиболее проницаемым даже при повышенной закрытой пористости. Низкие значения тупиковой пористости подтверждают высокую степень связности пустотного пространства и коррелируют с долей закрытых пор, что может указывать на возникновение их преимущественно в силу сечения изолированных пор границами рассматриваемых структур.  В целом, столь малый разброс значений пористости (менее 0,5 % относительно) позволяет считать поровый каркас практически изотропным по параметру пористости.

Геодезическая извилистость порового пространства демонстрирует ограниченные, хотя и устойчивые колебания от ~1,03 до 1,26. Эти значения указывают на то, что реальные пути фильтрации лишь немного длиннее прямого (геометрического) размера образца. Разброс средней извилистости между разными образцами незначителен (стандартное отклонение ~0,01, коэффициент вариации ~1 %), что подчёркивает воспроизводимость данного параметра. В плоскости напластования (оси X и Y) наблюдается нетипичная разница: средняя извилистость по оси Y чуть меньше, чем по оси X (на ~3–4 %), несмотря на расположение этих направлений в плоскости залегания породы. Одновременно ось Z (ось керна) ожидаемо показывает более высокую извилистость, что отражает влияние напластования. Тем не менее все полученные значения τ остаются низкими (~1,1), подтверждая высокую связанность поровых каналов.

Анализ путей перколяции позволил получить дополнительную информацию о геометрии порового пространства, которая выходит за пределы чисто геодезических характеристик. Для каждого направления (X, Y, Z) было определено по 100 перколяционных путей, представляющих собой физически реализуемые траектории, по которым могла бы пройти частица сквозь поровую систему. В отличие от извилистости, отражающей только длину геометрической кривой, алгоритм перколяции учитывает минимальные размеры поровых горлышек, способных пропустить частицу определённого диаметра. На рис. 2 представлены на примере одного из образцов перколяционные пути по трём ортогональным направлениям (а – X, б – Y, в – Z) с наложенным цветовым градиентом, отображающим длину каждой траектории от входной до выходной поверхности. Во всех трёх направлениях перколяционные каналы формируют организованную, связную сетевую структуру с длинными непрерывными потоковыми зонами, без резких локальных искажений или пятен, которые могли бы свидетельствовать о наличии зон, требующих обхода или указывающих на локальные барьеры.

Рис. 2. Визуализация пространственного распределения части путей перколяции и интегральное градиентное отображение длины путей по осям Х, Y, Z

На рис. 3 показано распределение скоростей фильтрационного потока; во всех случаях видны схожие вытянутые области высоких скоростей, соответствующие «магистральным» каналам потока. Это означает, что в образцах присутствуют направленные пути фильтрации с минимальными геометрическими препятствиями, и подтверждает, что степень связности порового пространства высока в любом направлении. Таким образом, несмотря на слабую анизотропию фильтрационных свойств (см. ниже) сама геометрия порового каркаса близка к изотропной – как по интегральным показателям (пористость, извилистость), так и по структурной организации перколяционных путей.

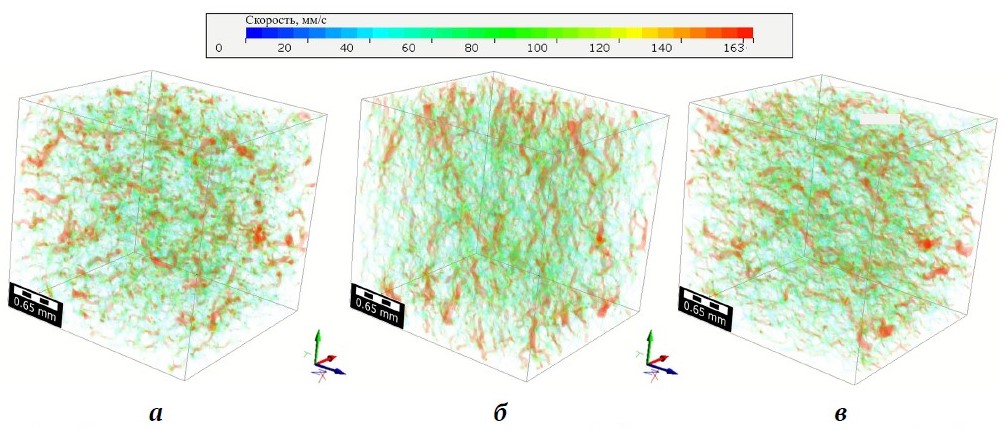
Рис. 3. Визуализация пространственного распределения скоростей фильтрационных потоков по осям Х, Y, Z

В отличие от пористости, фильтрационные свойства проявляют слабовыраженную, но отчётливую анизотропию. Расчётные значения проницаемости (см. табл. 1) различаются между тремя осями. Наблюдается слабое проявление нетипичного типа анизотропии: одно из горизонтальных направлений X оказалось менее проницаемым, чем вертикальное направление Z, а предпочтительный фильтрационный поток ориентирован вдоль оси Y. В количественном отношении эта анизотропия невелика (отношение k_Y : k_X ≈ 1,3, k_Y : k_Z ≈ 1,2), но она устойчиво воспроизводится во всех образцах. Разброс значений проницаемости между разными образцами для каждой оси не превышает 0,01 Д (относительный коэффициент вариации < 0,5 %), благодаря чему выявленная разница между X, Y и Z является статистически достоверной и обусловлена микроструктурой породы. Это подтверждается и независимыми физическими экспериментами: лабораторные измерения на керновом материале показали проницаемость ~5,6 Д вдоль оси керна и ~6,1 Д в плоскости напластования XY. Хотя абсолютные значения в лаборатории несколько выше, соотношение между направлениями аналогично модельным данным, указывая на наличие слабой, но устойчивой трансверсальной анизотропии фильтрационных свойств породы. Хорошее соответствие результатов численного моделирования и эксперимента свидетельствует о корректности применённого цифрового подхода и адекватности модели для воспроизведения реального фильтрационного поведения образцов.

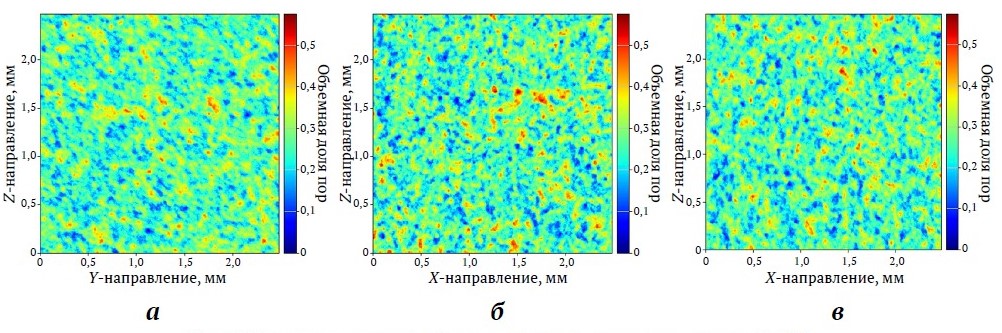
Рис. 4. Распределение усреднённых значений пористости по осям Х, Y, Z

Картограммы пористости, полученные путём послойного усреднения по каждому направлению, представлены на рис. 4. Цветовая шкала отражает локальные значения пористости; синий соответствует минимальным значениям, красный – максимальным. По всем трём проекциям (а – YZ, б – XZ, в – XY) распределение значений сохраняет близкую структуру: на изображениях преобладают зоны с равномерным переходом от голубых к зелёно-жёлтым оттенкам, что соответствует значениям пористости около среднего значения. Локальные отклонения встречаются, но не формируют кластеров или выраженных направленных аномалий. Это свидетельствует о том, что структура порового пространства сохраняет близкий к изотропному характер не только по интегральным значениям, но и по распределению пор в объёме. Это позволяет предположить, что наблюдаемые различия в фильтрационных свойствах связаны не с пористостью как таковой, а с геометрией соединения пор – извилистостью, шириной горловин и степенью их связности.

Результаты показывают, что при одинаковой пористости различия в геометрии порового пространства (извилистость, размер каналов, связность) существенно влияют на проницаемость. Направление Y демонстрирует наибольшую проницаемость, сочетая минимальную среднюю извилистость и немного больший средний диаметр поровых каналов (см. табл. 1). Согласно формуле Козени–Кармана (в модификации Беккера) для однородной пористой среды:

k = φ³/(1 − φ²) · 1/(Cτ²S₀²),

где φ – пористость; C – константа структуры; τ – коэффициент извилистости; S₀ – удельная поверхность зерен. Соотношение является качественной иллюстрацией известных взаимосвязей, однако часто используется для первичной оценки свойств поровых сред. Пористость в рассматриваемых образцах почти постоянна (φ ≈ 26 %), а различия в удельной поверхности можно оценить через характерный размер порового канала. Приняв, что S₀ обратно пропорциональна среднему диаметру пор d, формулу можно упростить до: k ∝ d²/τ². Это отражает интуитивно ожидаемую зависимость: увеличение поперечного сечения потока (больший d) и уменьшение извилистости (меньший τ) повышают проницаемость. Действительно, качественно наблюдаемая анизотропия согласуется с этой моделью: направление Y имеет крупнейший средний диаметр пор (~22,8 мкм) и наименьшую извилистость (~1,08), благодаря чему и демонстрирует максимальное k.

Однако количественно классическая модель недооценивает эффект. Расчёты показывают, что при снижении τ всего на ~3 % и увеличении d на ~1 % (как в направлении Y относительно X) относительный рост k должен составить лишь около 10 %, тогда как по моделированию он достигает ~30 %. Аналогично перколяционная модель Каца–Томпсона (связывающая проницаемость с квадратом критического радиуса порового канала) предсказывает почти равные значения k для X и Y ввиду практически одинакового размера «горлышек» (в рассматриваемом случае средний максимальный диаметр ограничивающих отверстий отличается менее чем на 1 %). Таким образом, стандартные модели не полностью объясняют полученную анизотропию, что указывает на наличие дополнительных факторов. Вероятно, более высокая проницаемость по оси Y обусловлена тонкой организацией поровых каналов, не отражённой напрямую в усреднённых параметрах d и τ (например, конфигурацией сети пор, распределением радиусов и т.д.). В направлении Y реализованы более прямые и сквозные потоки благодаря литологической упорядоченности структуры, тогда как в направлении X часть каналов перегорожена или отклонена. Иными словами, проницаемость слабосцементированных песчаников оказывается крайне чувствительной к изменению извилистости и связности пор: даже небольшое «выпрямление» каналов даёт непропорционально большой прирост k. Аналогичные выводы сделаны в работе [35], в которой показано, что в песчаниках и карбонатах логарифмическая зависимость между проницаемостью и пористостью имеет большой разброс и сильно зависит от сортировки и диагенеза. Это наблюдение подтверждается и в настоящем исследовании, что подчёркивает ограниченность использования только пористости как прогностического параметра. Аналогично и в более поздней работе [36], основанной на статистическом моделировании 13 000 пористых структур, сделан вывод о том, что корреляция проницаемости и пористости может быть недостаточной, особенно при пористости ниже 0,7, и что геометрические параметры, такие как извилистость и проводимость, при корректной формализации дают более точное описание фильтрационных особенностей порового пространства. Аналогичная связь пористости и проницаемости подчеркнута для нефтеносных песчаников в работе [37]. Особенно важно, что направление Y несмотря на минимальную открытую пористость оказалось наиболее проницаемым – что хорошо согласуется с гипотезами [38] о роли литологической упорядоченности и текстурной направленности в формировании эффективных каналов фильтрации. Это подчёркивает необходимость комплексного подхода к оценке коллекторских свойств, включающего не только классические петрофизические параметры, но и топологический анализ поровой сети, прямое гидродинамическое моделирование и морфологическую характеристику порового каркаса.

Для корректной оценки параметров порового пространства цифровой модели необходимо определить репрезентативный элементарный объём (REV, Representative Elementary Volume [39]) – минимальный объём пористой среды, для которого значения исследуемых характеристик (в данном случае пористости) становятся статистически устойчивыми и перестают зависеть от размера выборки. Знание этого параметра обеспечивает достоверность и воспроизводимость дальнейших вычислений, в частности, моделирования процессов фильтрации и оценки проницаемости.

Для численного определения REV использовался метод поэтапного разбиения цифровой модели на домены меньшего размера с последующим анализом распределения пористости в каждом из них. В рамках данного подхода трёхмерная бинарная модель (полученная после реконструкции и сегментации) последовательно разбивалась на кубические домены различного размера: от крупных (300 вокселей по ребру) до более мелких (10 вокселей по ребру). На каждой стадии разбиения определялась пористость каждого выделенного домена, после чего строилась совокупная кривая распределения значений пористости.

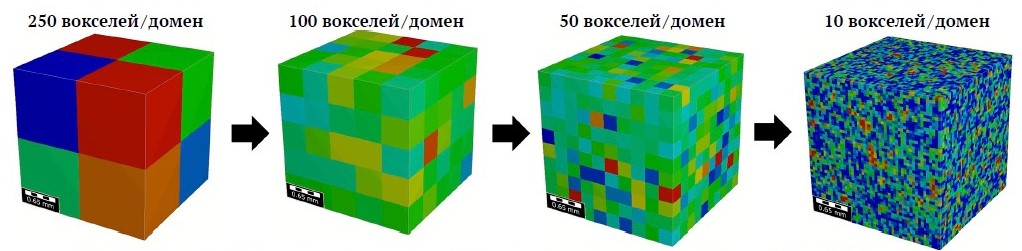
Рис. 5. Визуализация процесса определения репрезентативного элементарного объёма (REV) методом последовательного уменьшения размера доменов

На рис. 5 показан в общих чертах процесс разбиения исходных моделей на более мелкие домены. На рис. 6 отражены результаты количественного анализа пористости доменов: по горизонтальной оси отложены линейные размеры доменов (в вокселях), по вертикальной оси – рассчитанное значение пористости каждого домена. Каждая синяя точка соответствует пористости одного домена данного размера, а красная пунктирная линия – среднему значению пористости для соответствующего масштаба. Уменьшение разброса значений при увеличении размера домена свидетельствует о достижении статистической устойчивости параметра. Как видно из графика, при больших размерах домена (более 150 вокселей) разброс значений пористости между различными доменами становится минимальным и среднее значение стабилизируется. При расчётах ниже этого порога характеристики теряют устойчивость, что может приводить к некорректным обобщениям по модели. Все расчеты, выполненные в работе, были проведены на моделях с линейными размерами 500 вокселей. Также была проведена оценка REV на основе алгоритма контроля качества моделей песчаников, которая подтвердила достаточность используемого размера структур (N(REV) > 25). Данный подход учитывает соотношение наименьшей длины структуры к эффективному диаметру зерен [40] и обеспечивает надежную оценку REV для однофазного потока жидкости в песчаниках.

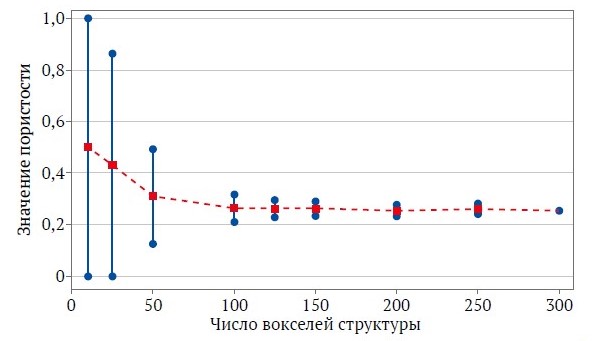
Рис. 6. Зависимость значения пористости от размера домена (числа вокселей по ребру) при определении репрезентативного элементарного объёма (REV)

3. Практические выводы и рекомендации

Выявленная анизотропия проницаемости связана с ориентированной структурой порового пространства в плоскости напластования. Выявленный профиль подтверждает целесообразность бурения горизонтальных скважин вдоль пласта – в направлении естественной текстуры пород, где сформированы наиболее проводящие фильтрационные каналы. Причем отдельное внимание стоит уделить выбору направления скважины в плоскости залегания в связи с проявлением нетипичной анизотропии: правильная ориентация стволов скважин позволит максимально задействовать высокопроницаемые пути и максимизировать дренаж пласта.

Высокая степень связности порового пространства и отсутствие барьерной анизотропии по проходимости частиц указывают на равномерность фильтрации во всех направлениях. Это значит, что фронт вытеснения (например, при закачке или продвижении газового/водного фронта) будет устойчивым и равномерным, без преждевременного прорыва в отдельных направлениях. Однородная внутренняя архитектура также благоприятна для полного дренажа пласта и эффективного вовлечения конденсата в поток. Минимальная доля изолированных пор (закрытая пористость < 0,5 %) и крупные поровые горловины снижают риск капиллярной изоляции конденсата – жидкая фаза не застревает в микропорах, а продолжает участвовать в фильтрации. Таким образом, обеспечивается более стабильная работа газоконденсатного пласта без резкого падения продуктивности из-за образования застойных зон конденсата.

Знание морфометрических характеристик поровых сетей позволяет с большей точностью подобрать оптимальный размер пропанта для гидроразрыва пласта и степень фильтрации закачиваемой воды. Таким образом предотвращаются закупорки пор частицами и вынос породного материала, что сохраняет проницаемость пласта. Применяемые методики цифрового анализа позволяют достоверно оценивать фильтрационно-ёмкостные свойства в условиях ограниченного кернового материала и могут обеспечить экспресс-оценку коллектора на этапе разведки: оперативное получение данных о пористости, проницаемости и анизотропии ускоряет принятие решений, сокращая зависимость от длительных лабораторных исследований.

Детальный анализ микроструктуры позволил оценить уязвимые места породы с точки зрения выноса частиц. Визуализация потоков показала наличие непрерывных высокоскоростных каналов фильтрации. В слабосцементированных песчаниках такие зоны концентрации потока могут вызывать повышенные напряжения на скелет и способствовать выносу зерен. Однако равномерное распределение пор и высокое общесвязное поровое пространство означают отсутствие резко выраженных «узких горлышек», где скорость локально возрастала бы экстремально. Это снижает риск внезапных пескопроявлений. Полученные результаты следует учитывать при проектировании режимов работы скважин: недопущение чрезмерных депрессий и равномерное распределение отбора по пласту будут способствовать стабильности стенок скважин. Интеграция полученных данных в геомеханические модели позволит количественно предсказать критические градиенты давления, при которых возможно разрушение породы, и тем самым минимизировать риск пескопроявлений.

4. Перспективы исследований

Дальнейшее развитие направлений исследований планируется за счет обоснования моделей извилистости порового пространства слабосцементированных песчаников и выявления её влияния на фильтрационные свойства этих пород. Планируется уточнить предельные условия применимости формулы Козени–Кармана и перколяционных моделей для рассматриваемых слабосцементированных коллекторов. Отдельной задачей является обеспечение масштабируемости параметров от микроуровня к масштабам керна и пласта, чтобы цифровые модели лучше отражали свойства на уровне пласта. Важным направлением является развитие цифровых моделей порового пространства для применения в моделировании многофазных или термо-гидромеханических процессов, что позволит учитывать натурные условия в коллекторе. Кроме того, не менее актуально развитие методов машинного обучения для автоматического прогнозирования фильтрационно-ёмкостных свойств по данным микроструктурного анализа.

С прикладной точки зрения одним из ключевых направлений дальнейших исследований является разработка протоколов экспресс-оценки проницаемости по цифровым моделям. Важной задачей является интеграция результатов цифрового моделирования в геолого-гидродинамические модели месторождений, особенно при ограниченном объёме исходных данных. Практическую значимость представляет адаптация методики на породах со сложной и неоднородной поровой структурой (например, карбонатах и трещиноватых песчаниках), что позволит распространить подход на более широкий класс коллекторов.

Заключение

Проведенное исследование анизотропии фильтрационно-ёмкостных свойств слабосцементированных песчаников газоконденсатного месторождения на основе цифрового анализа керна позволило получить новые данные о взаимосвязи микроструктуры порового пространства и фильтрационных характеристик. Комплексный подход, включающий микротомографию, 3D-моделирование и численные расчёты, подтвердил высокую точность цифровых методов при оценке коллекторских свойств, особенно в условиях ограниченного кернового материала, а также позволил сделать ряд выводов, важных для оценки коллекторских свойств и оптимизации разработки пласта.

1. Показатели открытой пористости практически идентичны во всех направлениях (~26 %), однако проницаемость демонстрирует слабую, но устойчивую нетипичную анизотропию. Наибольшие значения проницаемости наблюдаются вдоль одного из направлений в плоскости напластования, что связано с пониженной извилистостью и размером пор в этом направлении.
2. Показано, что при одинаковой пористости проницаемость существенно зависит от извилистости каналов, ширины горловин и связности пор. Классические модели типа Козени–Кармана недооценивают влияние этих факторов, что подчеркивает необходимость комплексного анализа морфологии порового пространства.
3. Оптимальное направление горизонтальных скважин должно учитывать выявленные особенности анизотропии проницаемости (отличие до 30% в разных направлениях) для максимизации дренажа, что позволит максимально задействовать наиболее высокопроницаемые пути по направлению к скважине, будет способствовать снижению депрессии при одинаковых темпах отбора и поможет улучшить охват пласта при закачке рабочих агентов.
4. Установленная равномерность структуры порового пространства, включая диаметр фильтруемых частиц, способствует минимизации рисков пескопроявлений благодаря снижению локальных скоростей фильтрационного потока. Кроме того, низкие значения закрытой пористости уменьшают вероятность капиллярного запирания конденсата.
5. Цифровые методы позволяют оперативно оценивать свойства коллектора на этапе разведки и минимизировать неопределённости при дефиците керна. При этом требуется минимальный объем образца (от 5 мм³), что критически важно для шельфовых месторождений с дефицитом кернового материала. Полученный широкий спектр данных может оперативно интегрироваться в гидродинамические модели, значительно повышая их прогностическую способность. Результаты численного моделирования хорошо согласуются с лабораторными измерениями, подтверждая достоверность подхода для прогнозирования фильтрационных свойств в сложных геологических условиях.

Таким образом, работа демонстрирует эффективность цифровых технологий для изучения анизотропии коллекторов и предоставляет инструменты для оптимизации разработки месторождений, особенно в условиях шельфовой добычи, где доступ к физическим образцам ограничен, а требования к надёжности прогноза – повышены. Дальнейшие исследования могут быть направлены на уточнение моделей извилистости и масштабирование результатов на масштаб пласта.